Cage Splitting
With Innies and Outies, we were looking out for single cells poking into a block or protruding outwards. We said that a block can be any combination of adjacent units (as long as they don’t overlap, like a row and a column). Sometimes, there just won’t be a single cell in one cage.
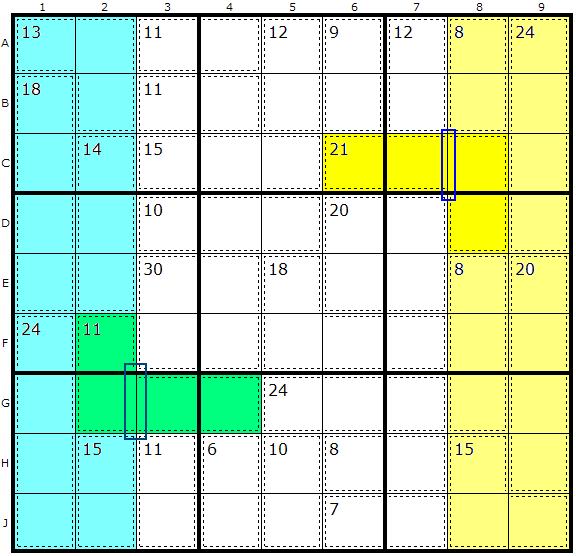
In this example, which is the "Tough" example on the Killer Solver, we have two cage splitting examples. A side note: because the cage pattern is symmetrical you should be able to find and use this strategy twice. Not all Killer puzzles are symmetrical, however, but it is worth looking out for.
Lets look at the yellow block - a 2 column block. We can see the straight line dividing columns 7 and 8 and just one place where a cage pokes out. The sum of all the yellow cages - less the outie - is 75. So we now know that C8 and D8 must add up to 15 (90-75). This allows us to split the cage into two 2-cage cells, 15 and 21-15=6, the outie half. So 3,6,7,8 and 9 can be removed from C6 and C7 and 1,2,3,4 and 5 can be removed from C8 and D8.
Similarly, the 2-column blue block has a symmetrically placed outie 4-cage summing to 11. The split gives us 6 as the value of the innie (F2,G2) and 5 as the value of the outie (G3,G4).
Cage Splitting doesn’t often get us whole solutions, but together with combinations (our first strategy), it can dramatically reduce the possibilities in cells. Cage Splitting can leave behind an innie or an outie elsewhere in another direction, which is also useful.

In this example, which is the "Tough" example on the Killer Solver, we have two cage splitting examples. A side note: because the cage pattern is symmetrical you should be able to find and use this strategy twice. Not all Killer puzzles are symmetrical, however, but it is worth looking out for.
Lets look at the yellow block - a 2 column block. We can see the straight line dividing columns 7 and 8 and just one place where a cage pokes out. The sum of all the yellow cages - less the outie - is 75. So we now know that C8 and D8 must add up to 15 (90-75). This allows us to split the cage into two 2-cage cells, 15 and 21-15=6, the outie half. So 3,6,7,8 and 9 can be removed from C6 and C7 and 1,2,3,4 and 5 can be removed from C8 and D8.
Similarly, the 2-column blue block has a symmetrically placed outie 4-cage summing to 11. The split gives us 6 as the value of the innie (F2,G2) and 5 as the value of the outie (G3,G4).
Cage Splitting doesn’t often get us whole solutions, but together with combinations (our first strategy), it can dramatically reduce the possibilities in cells. Cage Splitting can leave behind an innie or an outie elsewhere in another direction, which is also useful.
Using Locked Sets to Split Cages
In trying to understand an idea kindly emailed to me I got a different brain wave altogether looking at the same puzzle. Cage Splitting, as described above, works by finding one cage that is half in and half out of a block. This limits the chances of finding an instance because either quite a few cages need to be lined up or many cells need to be solved. What if there were a way to expand the number of Cage Splits?
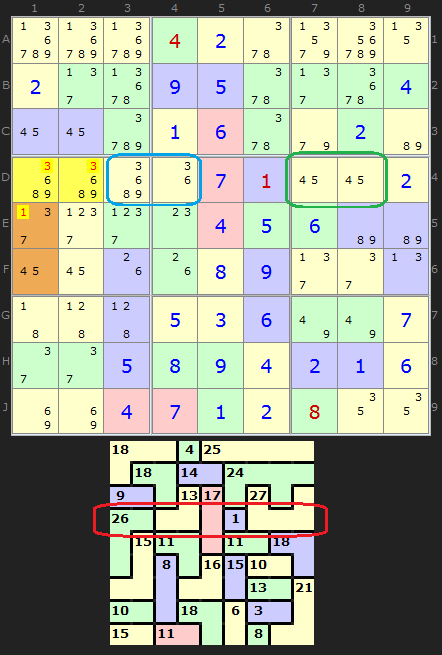
(Keyword: A Locked Set is and group of N cells that contain N number of different candidates. They must all 'see' each other as well. A solved cell is the simplest locked set as N=1.)
Consider row D in this puzzle. It doesn't look an especially worthwhile 'block' that might split in one place. We have a 7 in D5 which is nice, plus a 1 in D6. The 1 in C4 means we can calculate the value of D3/D4 (cyan box, which is 13 - 1, or 12). Now what about the last cage in the row? We have a 2 in D9 but the fascinating fact about this cage is the Naked Pair in D7 and D8. This is also a Locked Set just like any solved cell.
Because 4 and 5 are the only two values left for these two cells, we know they must sum to 9 - even though we don't know which way round they will be (but that's not important now). We can mentally split 5-cell cage with a value of 27 and know with certainty that the 'innie' cells contribute 11 to row D. So we can split the block in the first cage after all!
Using Locked Sets in this manner is extremely useful for Innies and Outies as well.
If the solver finds an example it will add this as an info alert:
(*note: the cage that includes C7 has been split to include it in the rows)
(*note: the cage that includes C7 has been split to include it in the rows)


Comments
... by: Pieter, Newtown, Australia
Thanks for all the daily puzzles and especially all the strategy explanations. Great way to learn!
Pieter
... by: steve voyce