| Main Page - Back |
|
From SudokuWiki.org, the puzzle solver's site |
3D Medusa
3D Medusa extends Simple Colouring (or 'Single's chains') into a third dimension. Simple Colouring looked for pairs of X in rows, columns and boxes. Wherever the chains led they stuck to the same candidate number. This is good for tracking an elimination when you have made notes on a paper Sudoku for a particular number but it limits the scope of the strategy. The way we extend the search is up through the bi-value cells which contain two different numbers. You can think of the different candidate numbers as existing in a third dimension lifting up from the page with 1 at the bottom and 9 at the top.
The devastating effect of colouring is that we are showing that ALL of one colour will be the solution. We don't know which set yet - but if any one of those cells becomes the solution we can know for certain ALL the cells of the same colour
The devastating effect of colouring is that we are showing that ALL of one colour will be the solution. We don't know which set yet - but if any one of those cells becomes the solution we can know for certain ALL the cells of the same colour
Rule 1 - Twice in a Cell
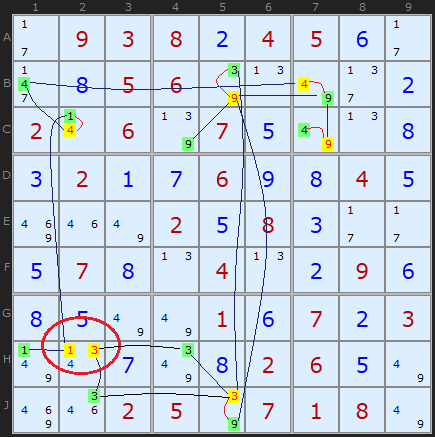
Continue to look for bi-value and bi-location candidates and you soon build up a web of connections. This is where the image of Medusa was perhaps attached to this strategy - her head being a tangle of snakes.
When you have built up a web of connections, alternating between two colours you might find a cell with the same colour set twice. This has been ringed in H2. Since we know that if yellow candidates have the potential to be ALL true we can't have a situation where two yellow numbers are competing for the same cell. This is a contradiction and therefore we can state that no yellow numbers can be the solution!
Rule 1 is: If two candidates in a cell have the same colour - all of that colour can be removed - and the opposite colour are all solutions
My old definition of Rule 1 (pre 2015) only made a negative assertion about the yellow candidates - they can be removed. But Steve Jacobs, also programming a solver, alerted me to the fact that all green candidates MUST be the solutions to their cells - a positive assertion. This is self-evident for bi-value cells (where only green and yellow exist and green becomes a Naked Single) but also for cells like H1 in the example. The 1 in H1 becomes a Hidden Single. This is true because of the binary either/or connections in the Medusa web. My solver will continue to only remove the yellow candidates - hidden singles will be eliminated in the next step - but for pen and paper solvers - go fill in the 'green' solved cells. Jacobs' corollary also applies to Rule 2 and Rule 6.
Note: this rule does not exist in Simple Colouring since the same number does not appear twice in the same cell.
As an exercise, try colouring any of the highlighted cells starting from a different position. You may end up swapping the colours around and you may find some new connections. But eventually - in this example - you will get two of the same colour on H2. This is a very powerful yet simple strategy.
Rule 1 is: If two candidates in a cell have the same colour - all of that colour can be removed - and the opposite colour are all solutions
My old definition of Rule 1 (pre 2015) only made a negative assertion about the yellow candidates - they can be removed. But Steve Jacobs, also programming a solver, alerted me to the fact that all green candidates MUST be the solutions to their cells - a positive assertion. This is self-evident for bi-value cells (where only green and yellow exist and green becomes a Naked Single) but also for cells like H1 in the example. The 1 in H1 becomes a Hidden Single. This is true because of the binary either/or connections in the Medusa web. My solver will continue to only remove the yellow candidates - hidden singles will be eliminated in the next step - but for pen and paper solvers - go fill in the 'green' solved cells. Jacobs' corollary also applies to Rule 2 and Rule 6.
Note: this rule does not exist in Simple Colouring since the same number does not appear twice in the same cell.
As an exercise, try colouring any of the highlighted cells starting from a different position. You may end up swapping the colours around and you may find some new connections. But eventually - in this example - you will get two of the same colour on H2. This is a very powerful yet simple strategy.
Rule 2 - Twice in a Unit
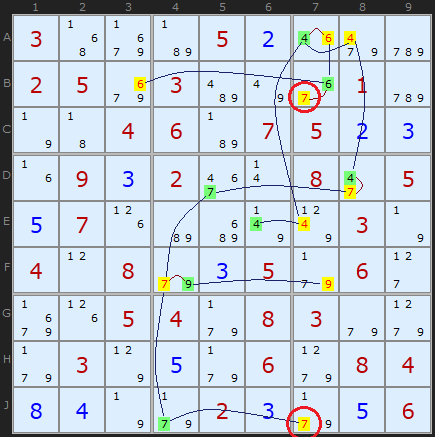
The example shows most of the links between bi-value and bi-location candidates, coloured between green and yellow. Ringed in red are two 7s in column 7. Since both cannot be true neither can be true and all yellow coloured candidates can be removed - and all green coloured candidates are solutions to their cells.
(Example requires three Medusa Rules 6 before Rules 2 comes into play)
Rule 3 - Two colours in a cell
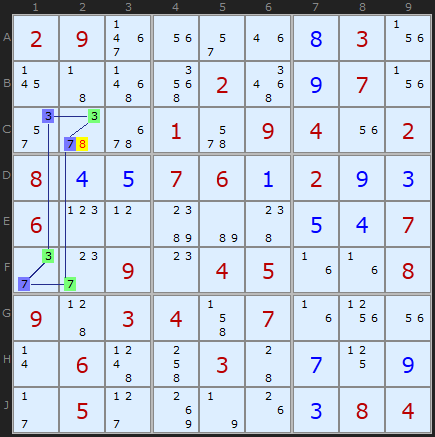
But 3D Medusa is not about loops, its about the network of links. This example just happens to be the same formation. We know that either ALL the blue candidates will be true, or ALL the green ones. If there are any another candidates in any cell with two colours, they cannot be solutions. Hence the 8 can be removed from C2. In Nice Loop terms, this is an off-chain elimination.
Simple Colouring cannot produce this elimination since it is restricted to a single candidate number.
Rule 4 - Two colours 'elsewhere'
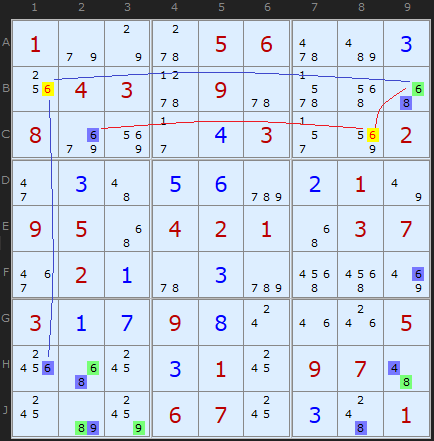
The 6 in B1 is removed because of the coloured 6s along the row in B9 and down the column in H1. In a similar way the blue 6 in C2 and the green 6 in B9 point to 6 in C8
This rule is shared with Simple Colouring.
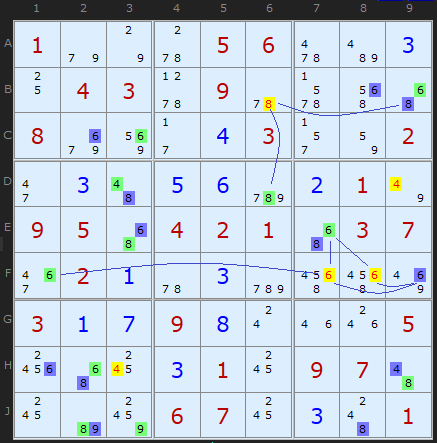
A few steps later in the same puzzle we get a cluster of 4s, 6s and an 8 using the same observation.
Since February 2015 I have combined Rule 4 with the old Rule 5. I want to thank a reader going by the name FallsOffRocks for pointing out that the old Rule exactly covered all the eliminations that Rules 4 did and was redundant. I've folded Rule 5 ('elsewhere') into 4 ('along a unit') and decremented Rules 6 and 7. A simplification! So from now on there are only 6 Medusa Rules. This also affects Simple Colouring.
Rule 5 - Two colours Unit + Cell
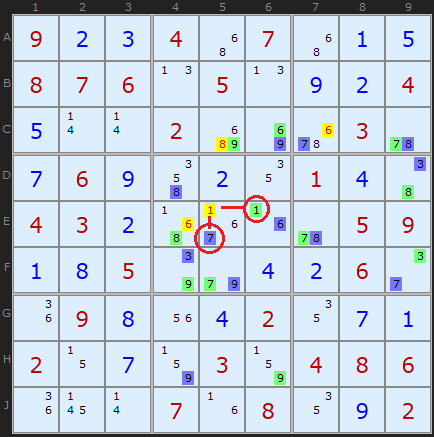
If an uncoloured candidate can see a coloured candidate elsewhere (it shares a unit) and an opposite coloured candidate in its own cell, it can be removed..
So its a combination of unit and cell - the colours green and blue are found looking along a unit and within the same cell. The example to the right demonstrates this with four eliminations.
The logic is very appealing. Consider 1 in E5. If 1 were the solution to the cell it would remove a green 1 from E6 AND a blue 7 from its own cell in E5. Since we know ALL blue or ALL green must be solutions we have a contradiction.
Rule 6 - Cell Emptied by Color

Rule 6 highlights in cyan the cell that catches this. You can see the 2 and 9 in cell D7 can see the yellow 2 in D3 and 9 in J7. (Yellow is used to show eliminated cells). All green coloured candidates are solutions to their cells.
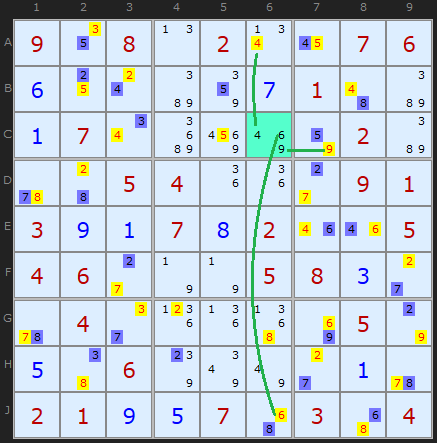
This puzzle has an amazing series of Medusa calls, using many different rules. It ends with Rule 6. I wanted to show a second puzzle to emphasize that the cell we are comparing the Medusa net to can have any number of candidates. These are 4,6 and 9 in C6. Green candidates have been turned yellow because they are eliminated, but you can see that the 4, 6 and 9 can all see the same color somewhere along the column or row.
You can be certain that it will be one color or the other, never equally both. Because this strategy is easier to spot and somewhat follows on from Rule 4, the solver looks for it before Rule 5. But too late to re-number them now. Well spotted Anton!
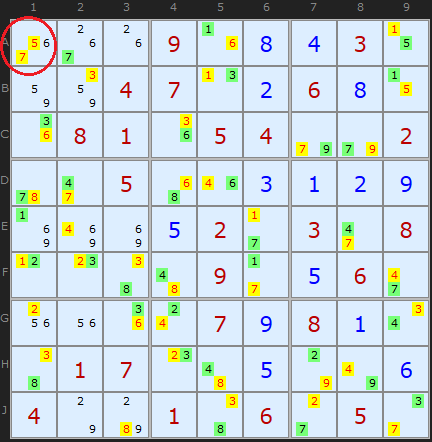
There are two candidates in A1 with the same color, 5 and 7. So All of those of that color can be removed.
However, the initial puzzle is not trivial and a very large number of steps are required before this mega medusa. Certainly an extreme grade.
3D Medusa Exemplars
These puzzles require the 3D Medusa strategy at some point and may have some other basic strategies but they are the easiest puzzles with examples. Restocked August 2025They make good practice puzzles.
- Exemplar 1 (Rule 1, score 155)
- Exemplar 2 (Rule 1, score 177)
- Exemplar 3 (Rule 2, score 184)
- Exemplar 4 (Rule 2, score 233)
- Exemplar 5 (Rule 3, score 155)
- Exemplar 6 (Rule 3, score 155)
- Exemplar 7 (Rule 4, score 154)
- Exemplar 8 (Rule 4, score 158)
- Exemplar 9 (Rule 5, score 151)
- Exemplar 10 (Rule 5 x2, score 162)
- Exemplar 11 (Rule 6, score 202)
- Exemplar 12 (Rule 6, score 212)