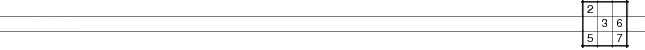
AIC with ALSs

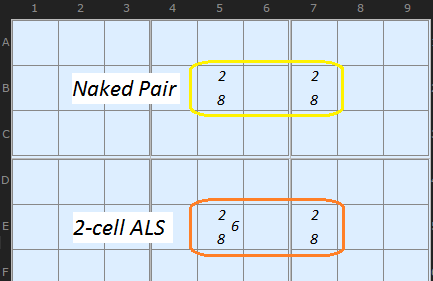
A Locked Set is a group of cells (that can all see each other) of size N where the number of candidates in those cells is equal to the size of the group. That is N cells contain N candidates. A solved cell or a clue is a Locked Set where N=1, but such a cell is not useful. The smallest useful Locked Set is a Naked Pair (where N=2) as in the [2,8] set in the diagram. The next smallest Locked Set is a Naked Triple (N=3) and so on.

An Almost Locked Set (ALS) is N cells containing N+1 candidates. In the context of Alternating Inference Chains in this solver, an ALS is of size N=2 and the number of different candidates in those cells is 3, although bigger ALS groups are possible. So an ALS of size 2 will be a two Conjugate Pairs plus one other candidate. In the diagram above the [2,8] pair are joined by a stray 6 which stops it being a useful Naked Pair.

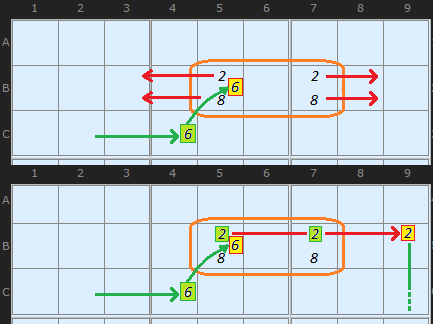
Lets continue with this ALS.

While solving a puzzle I am hunting around for Inference Chains and perhaps I find my chain turns ON the 6 in cell C4. That will remove all other 6s in the box including the 6 in our ALS. If that 6 is OFF then we create an on-the-fly Naked Pair.

Now, a Naked Pair eliminates candidates in the row or column (or box) it is aligned on so we can use this elimination property as part of our chain. This is the trick! By removing the 6 in B5 we fix 2 and 8 into those two cells so we can look along the row at other 2s and 8s and turn them OFF. This I do in cell B9. From there I can continue the inference chain. You get two cracks of the whip: check both branches - the 2s and the 8s in the pseudo Naked Pair.

A real life example now. This chain contains an ALS on the cells {G6,H6} (I used squiggly brackets to denote ALS as opposed to square brackets for Grouped Cells). 9s in row H are the entry point. We turn 9 ON in H2 which turns OFF the 9 in H6 - the extra candidate that makes the ALS an ALS. This gives us a Naked Pair of [5,7] that points up column 6 turning OFF the 7 in F6 and the chain continues.

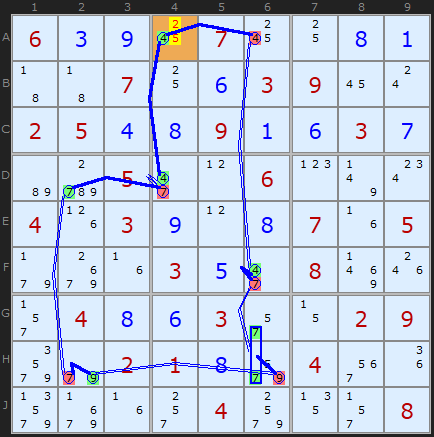
Ultimately we use Nice Loop Rule 2 to place 4 in A4
AIC on 4 (Discontinuous Alternating Nice Loop, length 12):
-4[A4]+4[D4]-7[D4]+7[D2]
-7[H2]+9[H2]-9[H6]+7{H6|G6}
-7[F6]+4[F6]-4[A6]+4[A4]
- Contradiction: When 4 is removed from A4 the chain implies it must be 4 - other candidates 2/5 can be removed

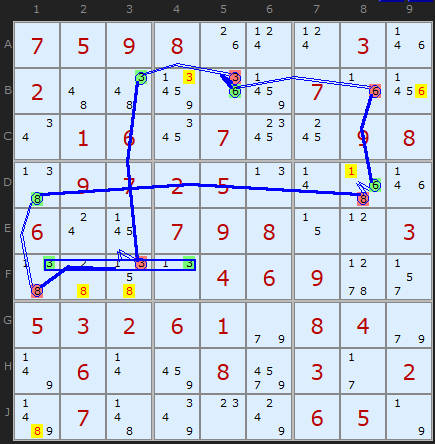
This second example uses a chain to kill off-chain candidates, which is Nice Loop Rule 1. The ALS is in {F1,F4} and consists of [1/3/8] and [1/3] respectively. We turn off the extra candidate, 8 in F1 to enable the Naked Pair to be formed.