Exocet

a.k.a. jExocet

Full Documentation Coming Soon

Exocet is a pattern that can often occur in very hard puzzles where the candidate density is very high. With few bi-value and bi-location candidates other strategies give up. Exocet takes on three or four candidate sets at a time which is just what is needed in the bottlenecks of extreme puzzles. My first implementation solved 51 out of 123 of the weekly "unsolvables" that were created by David Filmer. We will be replacing any stock known solvable with even harder puzzles.

Phil's concise description is impossible to better: When 2 of the 3 cells in a box-line intersection together contain 3 or 4 candidates, then in each of the two boxes in the same band but in different lines, if there are cells with the same 3 or 4 candidates, any others can be removed.

Order in Strategy List

My instinct is to put this near the end of the Extremes set of strategies but many of the eliminations in Exocet can overlap earlier strategies, I am told. I do not think I have implemented many of those but to test and improve I am putting it at the start of the extremes to give it more exercise. David Bird tells me it can go after the basics but that will have to wait until more variations are in place.

Credits

A number of people explored this strategy and its many variations. I am told the name was coined by forum participant Champagne. The pattern was first discovered by Allan Barker in the "Fata Morgana" puzzle^[1],[2]. My main source is the excellent JExocet Compendium written by David P Bird, available in fourteen downloadable documents on the EnjoySudoku Forum and David was kind enough to answer questions as well. I would also like to credit Phil's Sudoku Solver as a source of examples and help. Any other credits not mentioned, please email me.

I don't intend to duplicate David's work but just the parts implemented by the solver and re-expressed in my own way. Terms and references to the original will be supplied.

The Exocet Pattern

Lets start with the pattern.
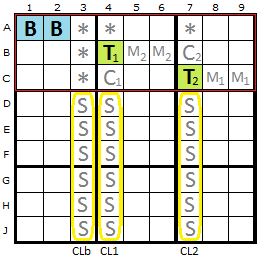
Pattern Rule 1
Two Base cells (B) exist in alignment in one box and usually contain three or four candidates *in total*. That could mean {1,2,3,4} + {1,2,3,4} but could also mean {1,2,3}+{2,3,4} or even {1,2,3}+{3,4}. I've not found an instance of two bi-value cells like {1,2}+{3,4} yet. To be explored.

Pattern Rule 2
We then check if there are two Target cells (T) that contain all the digits of the Base cell (plus any extras). The Targets cannot 'see' each other or the Base Cells. They must also be in the same Tier or Stack (group of 3x3 boxes in a row or column). The diagram highlights the top tier in red. There are only three possible cells for each Target given that they must not be 'seen'.

If Bases and Targets are aligned in a Tier (as in these diagrams) we look for three Cross-Lines that descend from the Targets and the cell not occupied by the Bases. These are marked in yellow - columns 3, 4 and 7. We are interested in the six cells outside the Tier (or stack). These cells are called S-Cells.

We will be talking about some of the other cells in the pattern as well, so lets introduce them. Each Target has a Companion cell marked with a C. Each Target has two Mirror Cells that are next to each opposite Target, marked M₁ and M₂.

Lastly, the asterisks are called Escape cells which can hold the candidates that are found to be false in the base.

Pattern Rule 3
To be a real Exocet pattern the Companion Cells must not contain the Base candidates, not even as clues or givens.

Pattern Rule 4
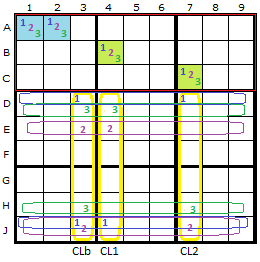
Now one last complication before we can be certain we have an Exocet. In the diagram I've set the Base candidates to be {1,2,3}. There is hopefully a scattering of these in the S-Cells. We want them to appear no more than twice each. If the Cross-Lines are columns we consider the rows where each Base candidate appears. These are called Cover-Lines and I've drawn all the cover-lines in the three colours of the three numbers.

I've stated that cover-lines are perpendicular to cross-lines. Usually they are, but to get the maximum number of elimination rules we can be flexible. It is possible that one Base candidate appears twice only in one column. If we were strictly perpendicular it would require two cover-lines, but all we want to do is "cover" the candidates, so in the single-column case we can "cover" them vertically. So the cover-line = the cross-line.
This will be useful later.

If an Exocet pattern can be confirmed, then following inferences occur:

• The two Target cells must contain different base digits.
  
• Mirror cells must contain the same base digits as their 'opposite' Target cells together with one digit that is false in the base cells.
  
• The two true base digits must each be true in two 'S' cells

As David writes, "These are a rich source of eliminations, some of which can be made immediately, and some that will become available later as the solution progresses. These can also be incorporated into AICs."

Note: When we talk about "true Base digits" we are talking about the final solution and knowing what those cells actually contain. We don't know that at the start but eliminations here might tell us more and we can go back through the Exocet check-list.

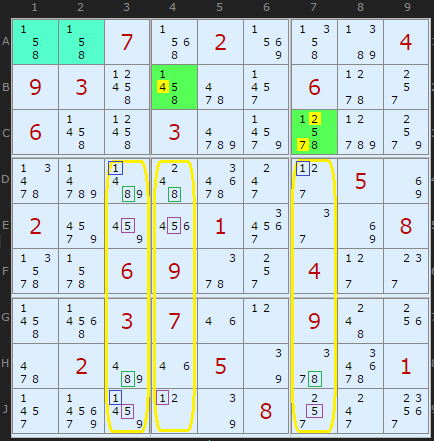
Any candidate in a Target cell that is not one of the Base candidates can be removed. That takes out the 4 in B4 and the 2 and 7 in C7

This example actually contains a whole raft of Exocet eliminations but they rely on another test called the Compatible Digit Check. That I have not implemented so I'm going to ignore those. I will come back to this example in the next update when I've understood this test.

Bird's definition: A base candidate that is restricted to only one 'S' cell cover house is invalid and is false in the base mini-line and target cells.

Bird's definition: A base digit in a target that must be true in the other target is false.

Which I take to mean if eliminations thus far reduce one target to one digit ON then it is strongly linked and eliminates like a single.

Bird's definition: A base candidate that has a cross-line as an 'S' cell cover house must be false in the target cell in that cross-line

Bird documentation states "If a mirror node contains only one possible non-base digit value, it is true in that node and false in the cells in sight of it."
I couldn't make this work without creating incorrect eliminations. By best implementation that doesn't create incorrect removals goes along the lines of "base digit missing from mirror node or base digits missing in the mirrored target cell".
See Tebo below in the comments for more insight.

Exocet Exemplars

These puzzles require the Exocet strategy at some point but are otherwise trivial.
They make good practice puzzles. Klaus Brenner finds.

• Exemplar 1, x1 (score 195)
• More as we find them...

---

¹EnjoySudoku forum
²See also Systematic Sudoku for Fata Morgana.