| Main Page - Back |
|
From SudokuWiki.org, the puzzle solver's site |
Introducing Chains and Links
Chains and Link are fundamental to many solving strategies and in this article I hope to draw together the ideas from all chaining strategies to show how chains and links can be identified and used. From chains we can deduce eliminations - but to build chains we need some logical building blocks to get us from one point on the board to another so we can say 'ah ha!' that IS connected to that, therefore....
We have a number of ways to build chains from different types of links. These vary in sophistication and define the difference between strategies. The goal is to discover a pattern on the board which leads to a contradiction or a positive or negative confirmation of a candidate.
So lets dive in
We have a number of ways to build chains from different types of links. These vary in sophistication and define the difference between strategies. The goal is to discover a pattern on the board which leads to a contradiction or a positive or negative confirmation of a candidate.
So lets dive in
Bi-Location Links
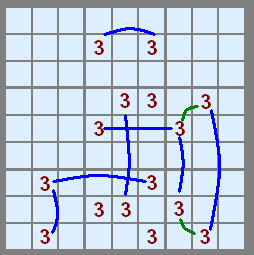
Drawn in blue and green are the possible links between certain candidates. The commonality is that some of these rows, columns and boxes there are only two candidates left. This means that one or other of these candidates will be the solution. We don't know which but each link described an EITHER / OR relationship. I've shown in green the links within a box, but often the link could be in a row or column AND a box, but it's not relevant which type of unit if the link is in both.
Links of this type are called Bi-location links, because the link is across two cells.
Bi-Value Links
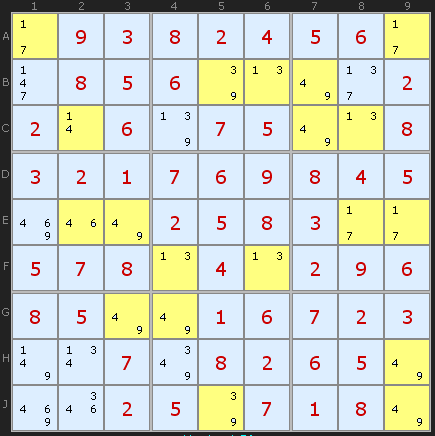
Such cells are known as Bi-value links. (Both bi-value and bi-location candidate pairs are also known as conjugate pairs (or complementary pairs) but these are term I am moving away from).
I don't need to draw a link between each pair value in each cell, it is implied by the nature of the two candidates in each cell.
Either / Or
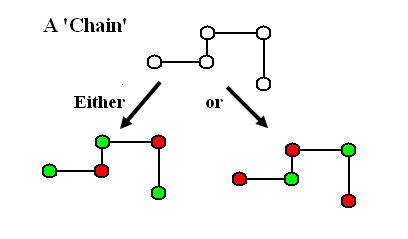
Chains, Loops and Nets
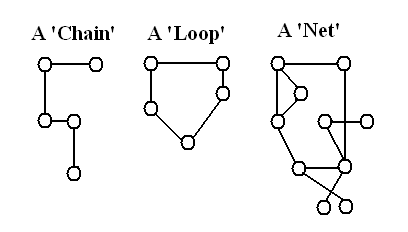
At any stage of the puzzle there should be several if not many possible chains. Only a few of them will be useful. Chains may not be connected, that is there is no bi-value or bi-location connection between two chains. Multi-Colouring takes advantage of two isolated chain nets. Forcing Chains take advantage of two or more linear chains to make an elimination.
Loops are linear chains with no start or end, or at least the start and end are arbitrary. The top left most candidate is used to express a definition of a Loop, which you will see as part of the solver output.
The table below groups the strategy according to the use of bi-value and bi-location links and whether linear or net-like chains are used. I also introduce Strong and Weak links in the next section.
Loops are linear chains with no start or end, or at least the start and end are arbitrary. The top left most candidate is used to express a definition of a Loop, which you will see as part of the solver output.
The Chaining Strategy Family
The table below groups the strategy according to the use of bi-value and bi-location links and whether linear or net-like chains are used. I also introduce Strong and Weak links in the next section.
| The strategies listed to the right use only bi-location links. Effectively that means they stick to one number and ignore all other numbers. You can think of them as working within one plane or dimension. |
|
||||||
| These strategies use bi-value AND bi-location links. Whereas the strategies before stick to one number these can move between number plains using bi-value cells and are hence 'two dimensional'. |
|
||||||
| These strategies use strong and weak links to bust out of the constraints of bi-value and bi-location only link connections. |
|
||||||
| These strategies use, in addition to bi-value and bi-location links, other more sophisticated links, although they are still two dimensional. | * Also uses exotic types of links such as Grouped Cells and Almost Locked sets. | ||||||
Part 2
Bi-value and Bi-Location links are not the end of the story. Chains that stick to only conjugate pairs are rather limited - but they are much easier to spot. You will be making good use of X-Wings, Y-Wings, XY-Chains and simple colouring to defeat moderately difficult puzzles. But to get the most out of chains we need to understand Alternating Inference Chains. These are well documented but first you should read the continuing article on Strong and Weak links.