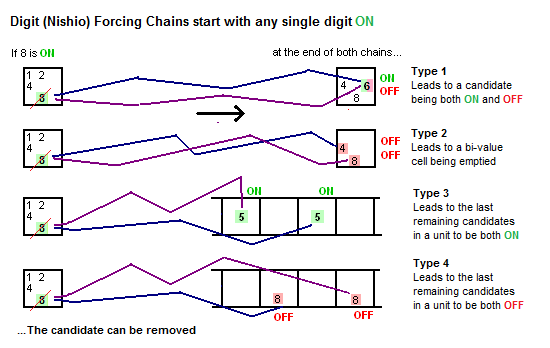
Nishio Forcing Chains

Nishio has a long history in the community as a semi 'trial and error' approach to very hard Sudoku bottlenecks, but in the implementation on this website it fits very nicely into the family of forcing chains and is a formal 'pattern' based strategy that uses AICs. In fact it is very close to Digit Forcing Chains since Nishio works on a single candidate as well. Where Digit Forcing Chains take a candidate and consider the consequences of the candidate being both ON and OFF, Nishio tries to find a contradiction when the candidate is merely ON. Two chains emanate from the candidate in different directions and try to join up later on another candidate. The rule is, if the start candidate is ON and this leads to another candidate being both ON and OFF it is indicating an impossible state of affairs. So the original candidate cannot be a solution.

A Nishio forcing chain is sometimes the exact reverse of a Digit Forcing Chain. If you look at the first diagram on that page you'll notice the first 'type' in the set of four ways a contradiction can be found is a destination candidiate that is ON when the start candidate is both ON and OFF.

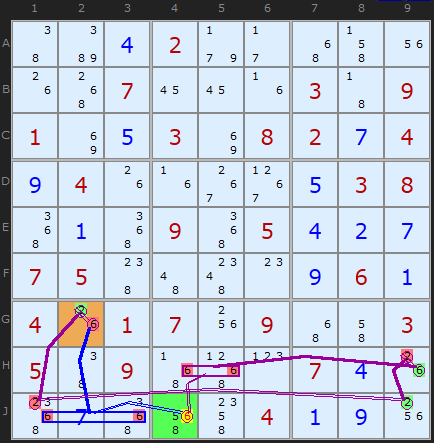
In this example the starting candidate is 6 in J4. The shorter blue chain simply says that when 6 in J4 is ON it removes the 6s in box 7 leaving 6 in G2 as the only remaining 6 and therefore the solution. On the other hand, the longer purple chain implies 6 cannot be the solution in G2. A 6 in J4 means 6s are removed from the rest of box 8 and that turns ON the six in H9. That forces 2 in J9 which in turn removes 2 from J1 making G2 2 and not 6.

Therefore the 6 in J4 cannot be a solution and it can be removed.