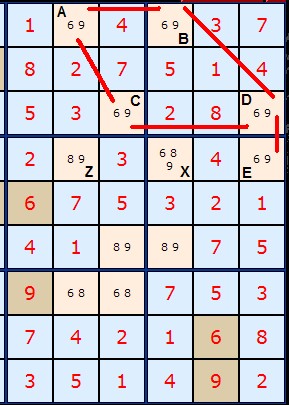
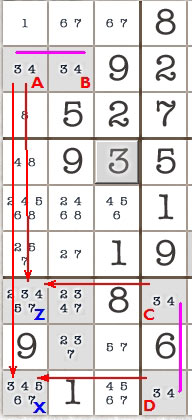
I coined Remote Pairs (back in 2005) to distinguish this new strategy/test/check, whatever, from the simpler more obvious pairs. Since first writing about it the strategy has been expanded in several directions and is more common than first thought. Pairs occur where two or more cells have the same two possible numbers. A locked pair is two such cells which lock each other in. For example, in the diagram on the right in the top row: 6 and 9 occur twice (labelled A and B) as a pair on the same row. This means the number 6 and the number 9 MUST both occur in these two cells. We can therefore eliminate other 6s and 9s from the same row. Same rule applies to boxes and columns. This forms the basis of Test 3 in my solver. On the diagram on the right I have marked all locked pairs with a red line. These are AB, AC, BD, CD and DE. You can load and view the whole of this board from the main Sudoku page. Look for Remote Pair Test in the drop-down list of examples. The point of this test/strategy is that we want to eliminate the 9 from cell Z and leave the 8. Can we do this logically, or must we guess? What about cell X which also looks like a candidate for removing the 6 and 9?

Remote Pair 1

To do this we must prove that A and E are themselves a locked pair. But how can we do this when they are not in the same row, column or box? We must also prove that B and E are NOT a locked pair, otherwise we'd have to remove the 6 and 9 from X as well. Visually we can see that if B is a 6 then D must be a nine so that E must be a 6. B and E are complementary pairs since they MUST have the same number, be it 6 or 9.
Likewise A and D.

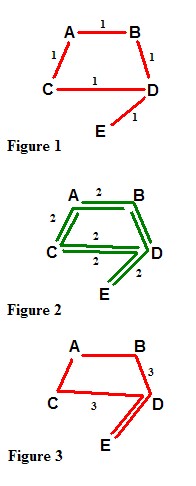
Consider Figure 1. We have five cells with the same pairs of numbers. Arranged in a pentagon as a network diagram each cell has four links to every other cell. I have drawn in red the links between locked pairs and ignored all other links. Let us say these links have a distance of 1 between the nodes. Now, in figure 2, we map all the pathways of distance 2. Valid pathways must be along the routes defined in Figure 1. What we are mapping here is all the complementary pairs, and I've drawn the links green. Topologically there cannot be ANY red links matching two locked pairs with distance 2. In figure 3, we are mapping all the possible pathways of distance 3. These paths represent connections between newly discovered locked pairs. There are only two possible paths in this example, and again they can only be between locked pairs at this distance. If we had more nodes we could carry on like this and look for distance 4 paths representing new complementary pairs but distance 4 is not possible in this example.

Remote Pair 2

However, we now know that we can show that AE is a locked pair if we can show that its minimum distance is an odd number (or distance mod 2 = 1 in arithmetical terms). They become a special locked pair I call a remote pair. Thus we may safely remove the 9 from Z. Because the distance between BE is an even number (2) we know we have a complementary pair and the information is useless for deciding the fate of X. Its important to remember numbers can be removed from any cell that both ends of the chain can see, so consider boxes as well as rows and columns.

Now the problem has been generalised we may proceed to code the rule into an algorithm. Test 9 on the solver page is the result.
Lets look at another example. This looks complicated because we have seven pairs

(marked A,B,C,D,E,F and G). Our targets are X and Z which can be got at by an attack from AD and AG.



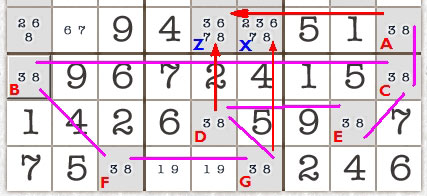
We would like to remove the 3 and 8 from Z and X. However, it is only safe to remove
the numbers from Z. Why? Because AD is an odd number of locked pairs from each other (ACED or ACBFGD). AG, whether you go via ACBFG or ACEDG are even numbers apart.

A word of warning though. It is essential that the line of attack is supported by a contiguous line of locked pairs. In the example on the right we have four pairs of 3/4 at A,B,C and D. However, while AB is connected and so is CD, there is no connection between the two groups. Therefore the elimination of the 3/4s on Z and X are not legal or logical. Credits I'd like to credit the person who posted the board I've worked from but they didn't leave a name. The debate on this problem is on this discussion forumdead link. Philip Frampton summarised the solution for Z most concisely. New: March 2007. Mihail Iusut has written a particularly interesting formal paper on the relationship between Remote Pairs and XY-Chains. You can download this here.

Remote Pairs Example