X-Cycles

X-Cycles are the start of a large family of 'chaining strategies' which are fundamental to solving the harder Sudoku puzzles. X-Cycles are strongly related to Simple Coloring.

A 'chain' is a series of links hopping from one candidate to another following very simple rules. A candidate can either be ON or OFF. That is, we either think it is a possible solution to that cell, or we do not. There are consequences to the rest of the board when we 'link' these two states.

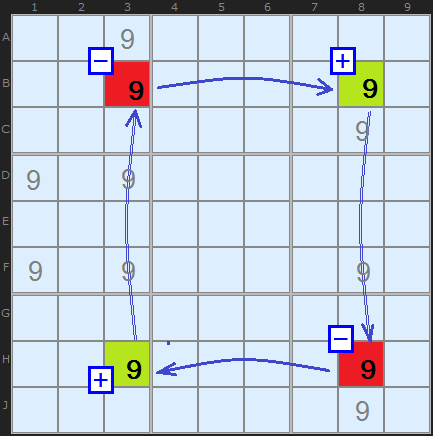
In the X-Wing structure in Figure 1, as an example, we can consider B3 to be OFF. This forces the the 9 in B8 to be ON since it's the only remaining 9 in the row. If B8 is ON then that removes the 9 in H8. Again, the consequence is to turn ON the 9 in H3 - and that closes the loop by confirming the 9 in B3 is OFF.

In this X-Wing example three things are apparent. I went round clock-wise, but I could easily make the same logical chain going round from B3 to H3 to H8 to B8 and back to B3. Also, could decide that the start cell was ON and follow the loop round. And lastly, B3 is arbitrary, I could start on any of those four cells.

Another important way of thinking about this situation is from the point of view of the links. When a candidate is turned OFF AND there are only two candidates in the unit, then we can create a Strong link, as between B3 and B8 (marked in a thick blue line) and H8 and H3. Because there are just two 9s in each row, we know that if one is not a 9, the other must be. A strong link is where:
!A => B (if not A, then B)

Weak links are the opposite:

A => !B (if A, then not B)

Strong and Weak links alternate just as candidates are turned OFF and ON. When we turn a candidate X ON we effectively remove ALL other candidates of X in ALL other units. However, when we turn a candidate X OFF it has no effect unless the unit has only two of X in it.

A "Cycle", as the name implies, is a loop or joined-up chain of single digits with alternating strong and weak links, as the X-Wing in Figure 1 shows.

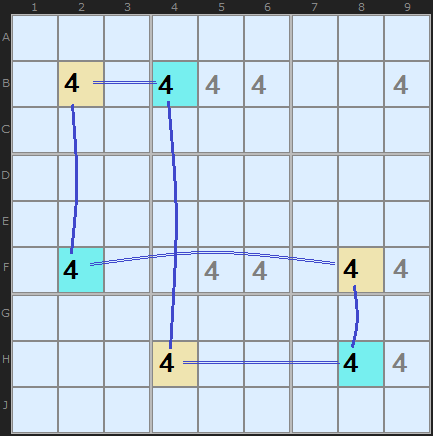
In Figure 2, we have a 2-2-2-formation Swordfish re-drawn to show the strong and weak links. The loop characterises the X-Cycle, and the strong/weak links alternate.

Nice Loops have evolved a notation which is useful when accompanying a diagram or as part of an explanation. X is, of course, the digit, and we use the row letter and column number notation to identify cells (e.g., B2, F8). The cells in the loop are linked with a minus to indicated X has been turned OFF, and a + to indicated X has been turned ON - you will see these colours on the solver. An example:

+x[cell 1]-x[cell 2]+x[cell 3]-x[cell 4]

The 2-2-2 Swordfish above can be expressed as:

+4[B2]-4[B4]+4[H4]-4[H8]+4[F8]-4[F2]

The only thing not explicit in this notation is that the last cell joins back onto the first cell. Thus, 4[F2]+[B2].
Loops can be of any length but they don't re-use any candidate.

Chains like these that go in a loop are called Continuous. They have three characteristics:

• Firstly, it doesn't matter which way you walk round the loop - clockwise or anti-clockwise
• Secondly, it doesn't matter which cell you start with (although the convention is to start with the top left-most cell)
• Thirdly, each cell could be ON or OFF - as long as you alternate.

Even with the convention of starting with the top left-most cell, there are four ways we could write down a chain:

• Clockwise with B2 ON +4[B2]-4[B4]+4[H4]-4[H8]+4[F8]-4[F2]
• Clockwise with B2 OFF -4[B2]+4[B4]-4[H4]+4[H8]-4[F8]+4[F2]
• Anti-clockwise with B2 ON +4[B2]-4[F2]+4[F8]-4[H8]+4[H4]-4[B4]
• Anti-clockwise with B2 OFF -4[B2]+4[F2]-4[F8]+4[H8]-4[H4]+4[B4]

I've deliberately used neutral colours in the diagram above (yellow and blue) not to given the impression there only one way to write the same chain. However, the solver will return very positive red and green highlighting but that's because it has discovered one of those four ways first and discarded the other three identical ways.

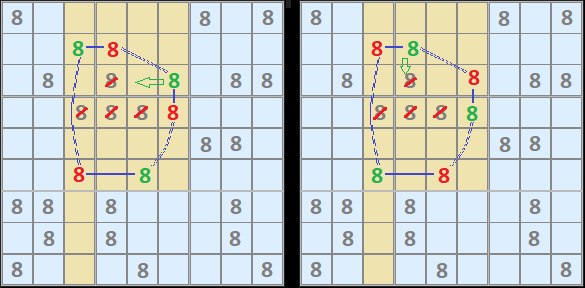
In this example of an 8-Cycle in Figure 3, I have split the two possible states into two diagrams.








This shows how each pair of strong links (that have only two candidates in the shared unit) can be set overall. No other combination of ONor OFF is possible.

The notation can either be, left
+8[B3]-8[B4]+8[C6]-8[D6]+8[F5]-8[F3]+8[B3]
or right
-8[B3]+8[B4]-8[C6]+8[D6]-8[F5]+8[F3]-8[B3]

The yellow cells are units where other 8s can be eliminated, which in this case correspond to the third column and boxes 2 and 5 because that's where the weak links are located. C4 is eliminated because of either B4 or C6

Nice Loops that alternate all the way round are said to be 'continuous', and they must have an even number of nodes. With a continuous X-Cycle, candidates are not removed from the loop since the loop does not have any flaws. Instead we are looking to eliminate on the units that can be seen by two or more cells that belong to the loop.

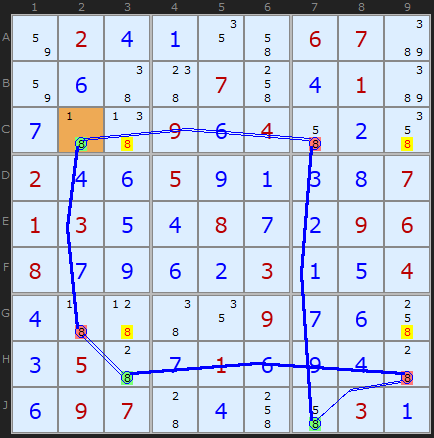
Figure 4 is a real-life example of an X-Cycle based on 8. The cells with links are in red and green. We can immediately see that C2/C7 is a weak link across the row because of the 8 in C3. G2/H3 is also a weak across the box because of the third 8 in G3. The last weak link is in box 9, J7/H9. Any other 8s in these units can be removed, which makes it a powerful technique. We end up with a loop containing only strong links – a result identical to a Colouring (Singles Chains) solution.

The output from the solver will contain the following information:

X-CYCLE (Alternating Inference Chain):
+8[C2]-8[C7]+8[J7]-8[H9]+8[H3]-8[G2]+8[C2]
- Off-chain candidate 8 taken off C3 - weak link: C2 to C7
- Off-chain candidate 8 taken off C9 - weak link: C2 to C7
- Off-chain candidate 8 taken off G9 - weak link: J7 to H9
- Off-chain candidate 8 taken off G3 - weak link: H3 to G2

In summary we can see that

• X-Wing is a Continuous X-Cycle with the length of four.
  
• Swordfish of the 2-2-2 formation is a Continuous X-Cycle with the length of six.
  

Although there are many other parallels as well.