WXYZ-Wing
This is an extension of XYZ-Wing that uses four cells instead of three. A.k.a. Bent Quads.
I am grateful to SudoNova posting below and StrmCkr who posted about this strategy way back when on this page. I only got round to appreciating the insights recently but the much expanded version of WXYZ is now in version 1.96+ of the solver. Previously I'd restricted the scope to a very narrow definition. Using one of my test libraries, the 50k set from Ruud, I increased the detection from 299 instances to 8313, so it is definitely worth looking out for.
I'm going to start with my narrow definition if only to show how this is an extension of the three-cell XYZ-Wing.
I am grateful to SudoNova posting below and StrmCkr who posted about this strategy way back when on this page. I only got round to appreciating the insights recently but the much expanded version of WXYZ is now in version 1.96+ of the solver. Previously I'd restricted the scope to a very narrow definition. Using one of my test libraries, the 50k set from Ruud, I increased the detection from 299 instances to 8313, so it is definitely worth looking out for.
I'm going to start with my narrow definition if only to show how this is an extension of the three-cell XYZ-Wing.

The easy principle is that each possible value of the hinge cell results in a Z value in one of the cells in the WXYZ-Wing pattern, thus leaving no room for a Z on any cell all four can 'see'.
That's the narrow definition and a glance at XYZ Wing will show you its the same idea plus one more cell. You could expand it to a five cell pattern and five numbers.
Now, lets consider StrmCkr's more general definition:
WXYZ-Wings can be considered as a group of 4 cells and 4 digits, that has exactly one non-restricted common digit. We use that digit (Z) to eliminate since at least one of Z will be the solution.
Now, lets consider StrmCkr's more general definition:
WXYZ-Wings can be considered as a group of 4 cells and 4 digits, that has exactly one non-restricted common digit. We use that digit (Z) to eliminate since at least one of Z will be the solution.
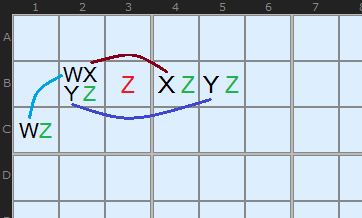
Well, a restricted digit is one where all the instances of candidate N in the pattern can see each other. On the diagram to the left I have connected the W candidates - because they share the same box, and I can connect the Xs and Ys as they share a row. Only Z is non-restricted because some of the Zs - ie the one in C1 CANNOT see the Zs in B4 and B5.
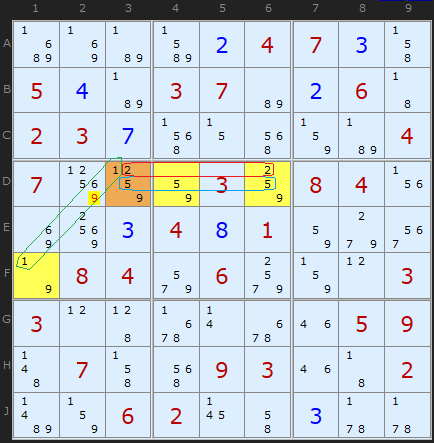
In the first example I show a classic WYXZ wing - in that it has all four candidates (1/2/5/9) in the hinge cell D3 marked in brown. The three outlier cells, marked in yellow each contain a 9 (our Z) plus some of the other four candidates.
I have also marked in rings the spread of candidates 1, 2 and 5. You will see that both 1s can 'see' each other because they are in the same box. The 2s can 'see' each other because they are on the same row and the three 5s can all see each other since they share the same row as well. That makes 1, 2 and 5 restricted in the four cell pattern.
Candidate 9 is different. At least one 9 (in F1) cannot see at least one other 9 - the 9s in D4 and D5. That makes it the only non-restricted candidate.
Any WXYZ elimination will always be made on the non-restricted candidate. We are looking for a 9 elsewhere that can see every 9 in the four cells of our WXYZ pattern. That 9 is on D2.
It is important to note is that StrmCkr's rule says nothing about the hinge requiring four candidates and the other cells two. Like Quads, we need in total four candidates in four cells. This is a four-cell Locked Set. StrmCkr makes this point in his second corollary, So lets look at some examples where the is a thinner spread of four candidates.
Interestingly, where Z is present in less than four cells, ie three or just two cells of the four - more eliminations are possible because there are less cells that the eliminated candidates need to 'see'. I believe my new implementation WXYZ gives more variants than the 10 StrmCkr lists as exemplars.
It is important to note is that StrmCkr's rule says nothing about the hinge requiring four candidates and the other cells two. Like Quads, we need in total four candidates in four cells. This is a four-cell Locked Set. StrmCkr makes this point in his second corollary, So lets look at some examples where the is a thinner spread of four candidates.
Interestingly, where Z is present in less than four cells, ie three or just two cells of the four - more eliminations are possible because there are less cells that the eliminated candidates need to 'see'. I believe my new implementation WXYZ gives more variants than the 10 StrmCkr lists as exemplars.
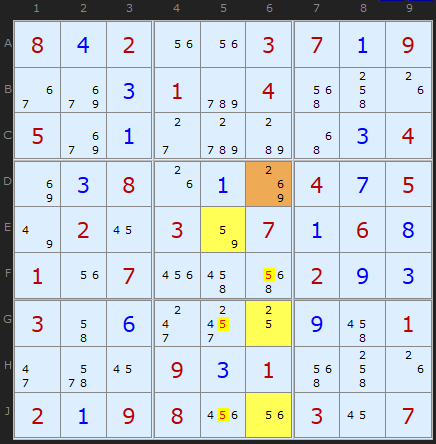
The second WXYZ example is orientated in columns rather than rows, but works the same. The hinge cell in D6 conspicuously fails to contain the non-restricted candidate 5, but no matter. Whatever the final solution of D6 a 5 is forced into either E5 or one of the two cells G6/J6. The outliers are nice easy pairs - like my original narrow definition, but the improvement is not needing 5 (Z) in the hinge every time.
The solver tells us
WXYZ Wing
The four cells {D6,E5,G6,J6} contain in total 2/5/6/9.
Candidate 5 determines the 'wing' cells (in yellow) and one or other of those 5s must be true. Therefore...
5 can be taken off F6
5 can be taken off G5
5 can be taken off J5
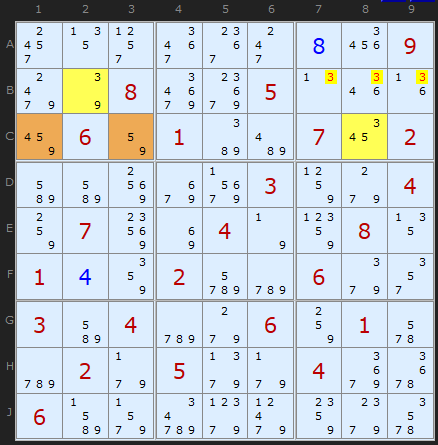
Here is an example where the non-restricted common digit is present in just two pincer cells. We don't have to worry about 3s 'seeing' the brown cells as they don't have a 3 in them. Consider how the hinge cell in C1 solves when each digit is looked at. Suppose C1 is 4. That makes C8 contain 3/5. C8 + C3 + B2 now becomes an Y-Wing - and eliminates 3s in the same way. Interesting!
The solver returns
WXYZ Wing
The four cells {C1,B2,C8,C3} contain in total 3/4/5/9.
Candidate 3 determines the 'wing' cells (in yellow) and one or other of those 3s must be true. Therefore...
3 can be taken off B7
3 can be taken off B8
3 can be taken off B9
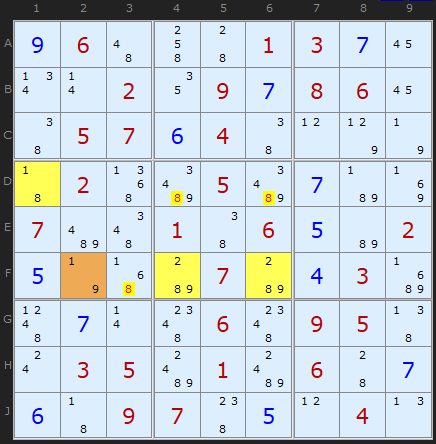
I'm ending this article with a nice Sudoku puzzle that has four Y-Wings an XYZ-Wings and four WXYZ-Wings. Here is the first of the later. It is worth following this through on the solver from the start.
Where next? StrmCkr's gives a theory example of a "double restricted common in a WXYZ-Wing when spanning the same band using box-box restraints" which I will explore at a future date. We can also go in the direction of a five cell VWXYZ-Wing but I think the next step is to exactly define the overlap and relationship with Almost Locked Sets - since a number of people have pointed out that these X-Wings are simple examples of ALSs.
Edit Sept 2015: There is an important post on WXYZ-Wings by Jon Welch which I recommend. I'm currently working through the implications but I'm definitely going to re-visit the Wings family again.


Comments