A Perfect Sudoku

I was asked to find a Sudoku solution - a board with all the numbers placed, which had a very specific property. The person emailing me was intending to make a woodwork piece with nine different types of wood arranged in a Sudoku formation. But to make it work he requested every number on the board should be in a different position relative to the 3x3 box each number appears in.

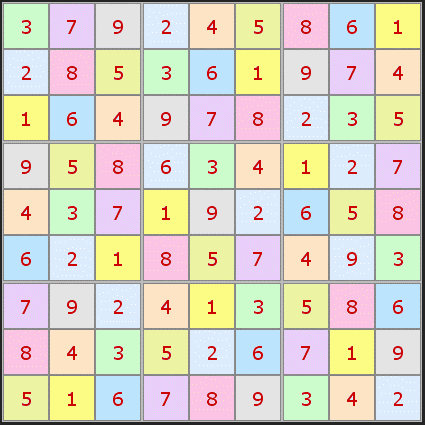
If you look at pretty much any Sudoku solution you will find some numbers that appear twice or more in the same position in a box. I searched through my library of many hundreds of thousands of puzzles and came across just one such puzzle solution. Here it is:

Now, why should this be so rare?

I'm sure it has some interesting mixture of a magic square and a Sudoku. Sudoku solutions have many symmetries so you can still juggle this around and maintain the same properties. The symmetries are:

1. rotation


2. reflection


3. transposing/shifting all of one number to another number, eg swap 1 and 2 etc


4. more interesting...you can swap rows or columns providing the swaps are within the same boxes. Eg you can swap column 1 with column 2 or 3 but not 5,6,7,8 or 9. Same with rows.


5. and lastly, you can swap boxes in groups of 3, eg you can swap the top three rows, with the middle three rows.

That's in case you want to make more versions of the essentially the same board.

You could, for example, reset this solution to be 123456789 along the top row just by substituting 3=1,7=2,9-3,2=4 etc etc for the whole puzzle.

Symmetries don't usually matter for solutions but the principle is the same, and more important, for a puzzle. Any puzzle mixed up by any or all of those symmetries, no matter how many times, will always solve the same way and have the same grade, even though it looks completely different. That's why there are only 4 billion or so possible Sudoku solutions - that are actually different - as opposed to the trillion, trillion ways of arranging them.

Work on this type of puzzle has lead me to create them and there is now a Colour Sudoku solver.