A Perfect Sudoku
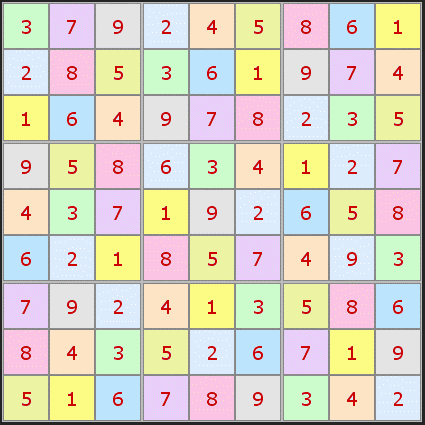
If you look at pretty much any Sudoku solution you will find some numbers that appear twice or more in the same position in a box. I searched through my library of many hundreds of thousands of puzzles and came across just one such puzzle solution. Here it is:
Now, why should this be so rare?
I'm sure it has some interesting mixture of a magic square and a Sudoku. Sudoku solutions have many symmetries so you can still juggle this around and maintain the same properties. The symmetries are:
That's in case you want to make more versions of the essentially the same board.
You could, for example, reset this solution to be 123456789 along the top row just by substituting 3=1,7=2,9-3,2=4 etc etc for the whole puzzle.
Symmetries don't usually matter for solutions but the principle is the same, and more important, for a puzzle. Any puzzle mixed up by any or all of those symmetries, no matter how many times, will always solve the same way and have the same grade, even though it looks completely different. That's why there are only 4 billion or so possible Sudoku solutions - that are actually different - as opposed to the trillion, trillion ways of arranging them.
Work on this type of puzzle has lead me to create them and there is now a Colour Sudoku solver.
I'm sure it has some interesting mixture of a magic square and a Sudoku. Sudoku solutions have many symmetries so you can still juggle this around and maintain the same properties. The symmetries are:
- rotation
- reflection
- transposing/shifting all of one number to another number, eg swap 1 and 2 etc
- more interesting...you can swap rows or columns providing the swaps are within the same boxes. Eg you can swap column 1 with column 2 or 3 but not 5,6,7,8 or 9. Same with rows.
- and lastly, you can swap boxes in groups of 3, eg you can swap the top three rows, with the middle three rows.
That's in case you want to make more versions of the essentially the same board.
You could, for example, reset this solution to be 123456789 along the top row just by substituting 3=1,7=2,9-3,2=4 etc etc for the whole puzzle.
Symmetries don't usually matter for solutions but the principle is the same, and more important, for a puzzle. Any puzzle mixed up by any or all of those symmetries, no matter how many times, will always solve the same way and have the same grade, even though it looks completely different. That's why there are only 4 billion or so possible Sudoku solutions - that are actually different - as opposed to the trillion, trillion ways of arranging them.
Work on this type of puzzle has lead me to create them and there is now a Colour Sudoku solver.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Charles Wyatt
Charles Wyatt
1-727-687-0263
Largo, Florida
P.S. I'm 80, retired and spend most of my time workinG on Sudoku puzzles
... by: Charles Wyatt
repeated numbers in the same location in boxes and you've duplicated numbers in the diagonals.
If you would be interested I have such aa puzzIe in a 3x3 9 number, 4x4 16 umber and a 5x5 25 number. I'm working on a 6x6 36 number now.
... by: wHack
... by: Rob W
However, I tried to take it even further. The example above has lots of "Parallel Pairs" - 4 & 1 in rows 8-9, 8 & 5 in cols 2-3, 6 & 3 in cols 4-5. Obviously, for a solve-able puzzle, one or more of these foursomes have to be provided as starter numbers.
Also tried to remove triplet values (e.g. 8, 6 and 5 in cols 7-8) but found that left far too few permutations to work with ... and caused my laptop to overheat!!!
It really is amazing the tricks you can pick up when you start rummaging.....
Cheers!
... by: Nanang