Y-Wing Chains

Strategies for Number Puzzles of all kinds

Main Page

Print Version

Solvers

Puzzles

Basic Strategies

Tough Strategies

Diabolical Strategies

Extreme Strategies

Depreciated Strategies

Str8ts

Other

Feedback

Donate

Order Now!

Order Now!

Y-Wing Chains

The Y-Wing strategy can be extended into chains. Remember, the Y-Wing consists of a pivot cell and two pincers. We keep the principle of the pincers exactly the same. The difference is that the pivot can be replaced by locked pairs.

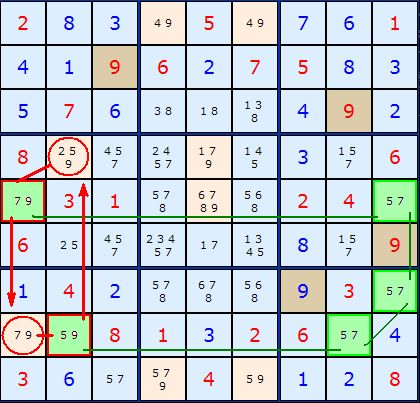
Our pivot chain for a Y-Wing must proceed at odd numbered cells (or even number of links). A Y-Wing is simply a chain with length = 1.

In Figure 1 we have a Y-Wing Chain marked out in green cells. The 5/7 pivot consists of three pairs of 5/7. The first 5/7 (in which ever order) is connected to the last 5/7 by a third 5/7 in the middle, and by definition this is a locked pair. If the first 5/7 is a 5 then the third one must be a 5 as well. Same goes for number 7.

Our pincer is based on the two green cells marked with a red border - the pairs 7/9 and 5/9. The principle of the Y-Wing says that any cells that both those can see we can eliminate the common number - in this case 9. The two cells marked with a red circle can be 'seen' by both and the 9 removed.

Y-Chain 1: Load Example or : From the Start

Go back to WXYZ-Wing

Continue to XY-Chains

Comments

Comments - Talk

Monday 8-Aug-2011

... by: Elce

Should paragraph 2 read: " Our pivot chain for a y-Wing must proceed at an ODD number of POINTS (ie an EVEN number of LENGTHS between the points)" ?
Or have I missed the point!!
Thanks for your great tips - I am trying to use them to help me solve a hard (v hard!) samurai sudoku ie 4 sudocku with an interlocking central sudoku - any clues for this greatly appreciated!!

Andrew Stuart writes:

The old fence-post issue. I've reworded that sentence. Appreciated