Strategies for Number Puzzles of all kinds
 
 
Print Version
 
Solvers
Puzzles
Basic Strategies
Tough Strategies
Diabolical Strategies
Extreme Strategies
Depreciated Strategies
Str8ts
Other
The Logic of Sudoku
Order Str8ts Book 1
Order Now!
Order Str8ts Book 2
Order Now!
  Digit Forcing Chains
This is the start of a family of strategies called Forcing Chains. As the name implies they are made from chains - or formally - Alternating Inference Chains which are simple ON - OFF- ON - OFF consequences. Chains can start with an ON or an OFF. When a candidate X it turned 'on' it immediately turns 'off' all other candidates it can see. When a candidate is in the 'off' state it might turn on another candidate if there is only one left in the unit it can see.

In the strategy Forcing Chains we look at the consequences of a candidate being first ON and then OFF, or a group of candidates in a cell being ON (Cell Forcing Chains) or a number being ON in all instances in a unit (Unit Forcing Chains). If the consequences of the chains are identical - that another canidate is always ON or always OFF - then we have a contradiction.

Before we look at specific examples, its worth going over the different types of attack in this family. In this diagram the starting cell is on the left - and an 8 is chosen. It is attacking either another digit (first two rows), a cell (middle two rows) or a unit (last two rows). In each attack the ends of the two chains are either ON or OFF.

If the two ends of the chain meet on the same digit, the we can remove that digit if the ends are OFF, or it's the solution to that cell if the chain ends are both ON.

 Family of Digit Forcing Chains
Family of Digit Forcing Chains
Likewise, we can attack a whole cell by finding two ON or OFF digits. If OFF, then the last remaining candidate is the solution - but this only works if there are 3 candidates in the whole cell. If ON, then we know that one of those two ON cells is the solution, so any other candidates can be removed.

And finally, the unit attack, based on the same number appearing three or more times in that unit. You will see the pattern now. If we can find two numbers that the chain ends say must be ON, then one of them is the solution and the rest of that number X can be removed from the unit. If there are three numbers left and we identify two numbers that are off, then the last candidate is the solution.

Digit to digit attack
In this article we have a very tough Sudoku which contains a neat series of Digit Forcing Chains of increasing complexity. The first is given in Figure 1.

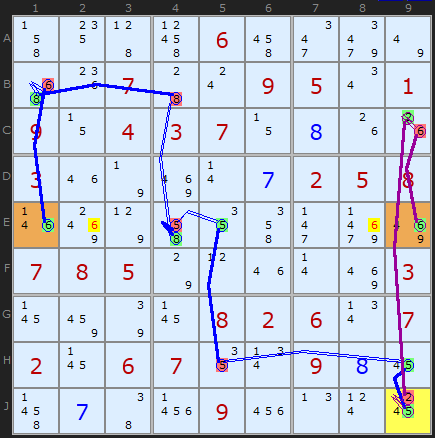
The 'digit' in this strategy is a single candidate - in this case the 9 in G2. We are looking at the consequences of this 9 being ON or OFF. If Off, then the only remaining 9 in the column is the one in E2. This would remove the 3 from that cell. Hense
-9[G2]+9[E2]-3[E2] (the blue chain).

Now, to be useful, we need to show that the 3 in E2 would also be removed if 9 in G2 were the solution (and turned ON). This is slightly more complicated but the chain only uses bi-value cells:
+9[G2]-9[G9]+8[G9]-8[A9]+2[A9]
-2[A2]+3[A2]-3[E2] (the purple chain)
9 in G2 forces an 8 in G9, a 2 in A9 and a 3 in A2 - voilà - that removes the 3 in E2.

Whether G2 is 9 or not the chains imply E2 cannot be 3 		Figure 1: Digit Forcing Chain
Figure 1: Digit Forcing Chain: Load Example or : From the Start

G2 also nets us another candiate in E2, the 1. The blue chain is the same - removing the 9 in G2 puts a 9 in E2 so no 1 is allowed.

A very similar purple chain gets us that 1 if 9 is turned ON:
+9[G2]-9[G9]+8[G9]-8[A9]+2[A9]-
2[E9]+1[E9]-1[E2]

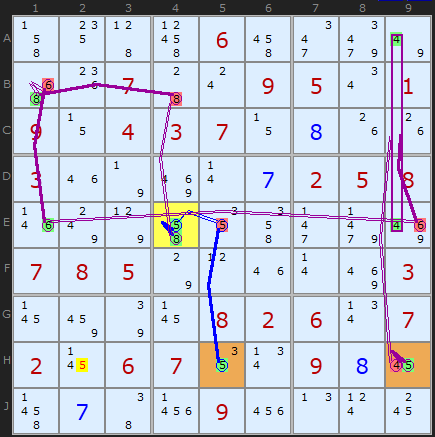
So, whether G2 is 9 or not the chains imply E2 cannot be 1 		Figure 2: Second Digit Forcing Chain
Figure 2: Second Digit Forcing Chain

Now we move to somewhere else on the board, the 5 in B2. This is a little more complicated as we have a grouped 'call' in 3 in C5/C6. But follow the chain round:
+5[B2]-5[B4]+2[B4]-2[H4]+3[H4]
-3[A4]+3[C5|C6]-3[C3]
The 5 in B2 means a 2 in B4. That forces a 3 in H4 turning OFF the 3 in A4. The only remaining 3s in box 2 are in C5 and C6. We notionally turn both of them ON and look along the row they are aligned on. If they are 'ON' (collectively) we can conclude 3 must be removed from C3

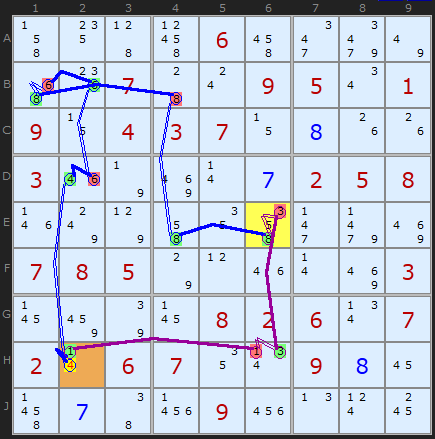
The other very simple blue chain removes the 3 in C3 because a 5 must go there when we turn the 5 off in B2. 		Figure 3: Third Digit Forcing Chain
Figure 3: Third Digit Forcing Chain

The final Forcing Chain in the sequence goes to G5 and the 7 there. The target is the 1 in G3. The blue chain is long but not hard. Removing 7 takes us round the board to G4 (+7), A4 (-7), A8 (+7), A9 (+8) and G9 (-8) forcing G3 to be 8 and hence not 1.

The second, purple chain contains a nice ALS cell on {1/5} in C3/G3 in the row. If 7 is ON in G5 then 3 will be removed from F3 leaving a Naked Pair of 1 and 5 in C3 and F3 - which of course removes the 1 from G3.

All in all
-7[G5]+7[G4]-7[A4]+7[A8]-8[A8]+
8[A9]-8[G9]+8[G3]-1[G3] and
+7[G5]-7[F5]+3[F5]-3[F3]+1{F3|C3}-1[G3]
Imply that G3 cannot be 1 whether G5 is 7 or not. 		Figure 4: Fourth Digit Forcing Chain
Figure 4: Fourth Digit Forcing Chain
Digit to Unit attack

Careful traversing of two chains might result in the chain ends resting on the same digit in the same row, column or box. The example here starts on G9 and winds it's way round to the 1s on row D. If the 5 in G9 is ON we get a result of 1 on D7. If the 5 in G9 is OFF we get a 1 on D1. Therefore, there cannot be any other 1s on that row. Three other 1s eliminated is a bit hit at this stage of the puzzle. The solver will return:

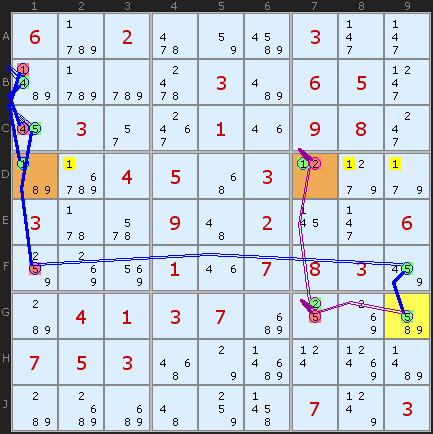
DIGIT FORCING CHAIN: because of G9, 1s in Row 4 are fixed on [D1,D7]
-5[G9]+5[F9]-5[F1]+5[C1]
  -4[C1]+4[B1]-1[B1]+1[D1]
+5[G9]-5[G7]+2[G7]-2[D7]+1[D7]
we can remove 1 from D2
we can remove 1 from D8
we can remove 1 from D9 		Digit Forcing Chains aim at a Unit
Digit Forcing Chains aim at a Unit: Load Example or : From the Start

But it doesn't end there. The very next step uses the new chain link made available by clearing those 1s away. With two 1s on row D we get a new conjugate pair and can extend the longer chain by one more link. This allows us to fix the 2s in column 7, giving us an elimination of 2 in H7.

DIGIT FORCING CHAIN: because of G9, 2s in Col 7 are fixed on [D7,G7]
-5[G9]+5[F9]-5[F1]+5[C1]-4[C1]
  +4[B1]-1[B1]+1[D1]-1[D7]+2[D7]
+5[G9]-5[G7]+2[G7]
we can remove 2 from H7
 Second Digit to Unit Forcing Chain
Second Digit to Unit Forcing Chain: Load Example or : From the Start
Continue to Cell Forcing Chains or Unit Forcing Chains....



 
Comments

Friday 16-Dec-2011

... by: Mike Leonard

If I load the puzzle of Figure 1, into the solver it reaches the point where 1 is remove from G3 by digit forcing chains. I do not understand why AIC did not find and remove it

Andrew Stuart writes:

Sometimes two chains are required where one is not enough. That is the case unless my one-chain AIC is missing a trick or is too restrictive in it's search and detection. But even if it is I find it helpful to break these two different approaches into different strategies.

Thursday 30-Dec-2010

... by: Lee

I have to agree with John, I don't see this as a very 'human' strategy.

There is nothing on this site which details the rules/patterns to look for to identify this strategy _without_ having to perform any kind of mental trial an error.

This leads me to argue that this 'strategy' is identified as a result of making an initial assumption rather than as a pattern that a person can identify to prevent the need to make that assumption.

Andrew Stuart writes:

It does require a lot of initial searching and mapping of available chains, but once the ideas are grasped, the concept seems fairly simple. One should map chain links initially - as this is required for any strategy in the chaining family.

Whether or not these are 'human' strategies in terms of paper and pencil is not really the issue. For the hardest puzzles these types of chains are absolutely necessary if an entirely logical solve path is to be identified. Perhaps they will be implemented purely by people developing such solvers and only of interest to them, but this site is dedicated to all strategies, computers or human.

Tuesday 21-Sep-2010

... by: wbngai

typing mistake: Paragraph 4, last cell G2 should be E2

Andrew Stuart writes:

Thanks! Changed

Thursday 26-Aug-2010

... by: John K. Landre

How do you find these chains?
It seems to me that, as with almost all extreme strategies, it is quicker to just start by assuming one of a possible pair is a certain value and then running the consequences until it either solves the puzzle or it runs into a contradiction. Of course, doing this sometimes does not have enough consequences to come to a conclusion with. So it helps to start this process by looking for a pair that 'runs' the puzzle, that is, that has as many connections to other pairs as possible.

Post a Comment using Facebook...
or post a Comment or Question here...
A confirmation email will be sent to you after submitting.

Your Name

Email Address - required for confirmation (it will not be displayed here)

Your comment or question

Please enter the
letters you see:
 arrow		Enter these letters
Remember me


Please keep your comments relevant to this article.
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted — no need to use <p> or <br> tags.


Article created on 17-March-2010. Views: 10110
This page was last modified on 2-June-2011, at 05:05.
All text is copyright and for personal use only but may be reproduced with the permission of the author.
Copyright Andrew Stuart @ Syndicated Puzzles Inc, 2011