SudokuWiki.org
Strategies for Popular Number Puzzles
Extended Unique Rectangles
Unique Rectangles can be larger structures than simple 2 by 2.
In this extension I show how the solver can now detect 2 by 3.
Just as a Naked Pair or Hidden Pair can be extended to a Triple, so can the cells that form Unique Rectangles.
A Triple is any three cells with a total of three candidates left. That doesn't always mean
[1,2,3] + [1,2,3] + [1,2,3]
Which is exactly three candidates in three cells. Other Triples will have some digits missing, like
[1,2,3] + [1,2,3] + [2,3]
[1,2] + [1,2,3] + [1,2,3]
[1,2,3] + [1,2] + [2,3]
And the ultimate skinny triple will have two out of three in each cell:
[1,2] + [1,3] + [2,3]
But all of these have - in total - three candidates in three cells.
In this extension I show how the solver can now detect 2 by 3.
Just as a Naked Pair or Hidden Pair can be extended to a Triple, so can the cells that form Unique Rectangles.
A Triple is any three cells with a total of three candidates left. That doesn't always mean
[1,2,3] + [1,2,3] + [1,2,3]
Which is exactly three candidates in three cells. Other Triples will have some digits missing, like
[1,2,3] + [1,2,3] + [2,3]
[1,2] + [1,2,3] + [1,2,3]
[1,2,3] + [1,2] + [2,3]
And the ultimate skinny triple will have two out of three in each cell:
[1,2] + [1,3] + [2,3]
But all of these have - in total - three candidates in three cells.
Type 1
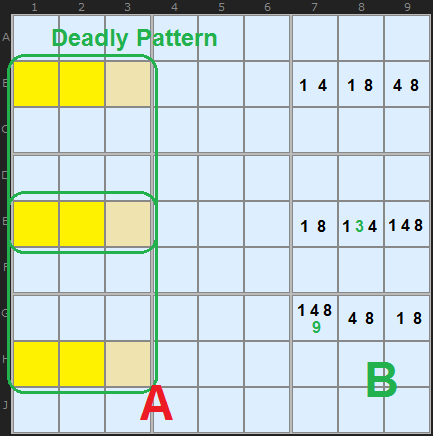
Note: it must occupy exactly three rows, three columns and three boxes.
To the right labelled B I've marked out a candidate distribution of 1s, 4s and 8s. For each row and each column you'll see a Triple. If we've arrived at this state we're in trouble because there are many ways to settle those cells in all combinations of 1, 4 and 8. The only thing that saves us are the extra candidates marked in green.
Here's how we go from the 3 by 3 ideal pattern to the much more likely 2 by 3 version: Take away any one of the columns with numbers and you still have a multiple solution problem. For example, if we took away column 8 (and ignored the green extra candidates for a moment), we could still fill column 7 with 1 + 8 + 4 (going down the rows), 4 + 1 + 8 and 4 + 8 + 1. Same for column 9. We could fill it with 4 + 1 + 8 or 4 + 8 + 1 or 8 + 4 + 1. If you take any column away it looks like the problem stays a problem. So conclusion - don't worry about looking for 3 by 3 Deadly Patterns - they will come out in the wash when you find 2 by 3.
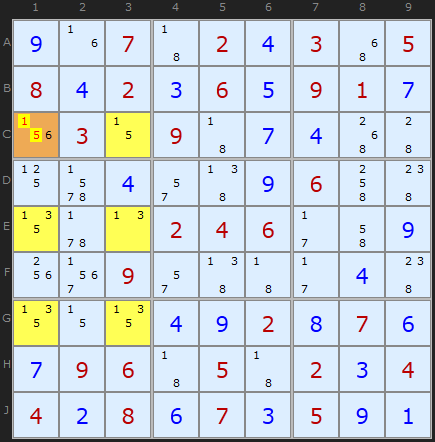
In this first example we have an Extended Deadly Pattern based on the three candidates {1,3,5}. The yellow cells mark the pattern. Notice this pattern is vertical like the theory example above - but as we are not looking for (and don't have) a 3 by 3, we need to look out for the pattern working horizontally as well. One of these is below.
The only type of UR I've implemented in the solver, so far, is Unique Rectangle Type 1.
This says that the odd cell out - the cell with an extra candidate or two - is the key. Those extra candidates must be part of the solution. If they didn't exist we've have a full Deadly Pattern and we need to avoid that at all costs. So 6 in C1 is the extra candidate - it must be the solution, so we can remove 1 and 5 from C1 and progress.
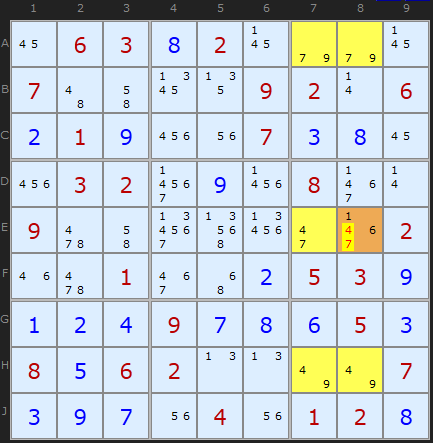
Here is a similar Extended Unique Rectangle based on the cells AEH78 (which just means cells on rows A, E and H and columns 7 and 8). The Triple is {4,7,9} and we have 1 and 6 - on cell E8. That's the get-out-of jail card avoiding the bigger Deadly Pattern. Take away the 4 and 7 from E8 and we're back into single solution territory.
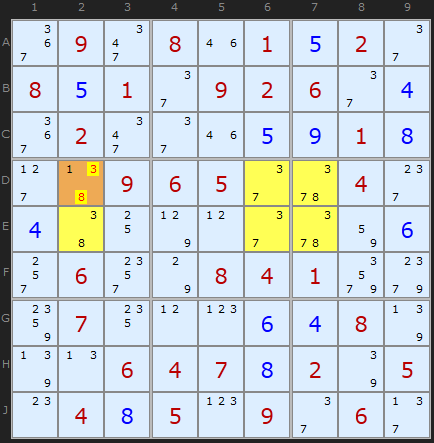
Finally a horizontal example.
The Triple {3,7,8} sits over the two rows D and E. There is a mixture of bi-value and tri-value cells but we clearly have two triples with the same values very close to each other. We have to use the extra candidates provided. There is a lone 1 in D2 that gets us out of trouble.
Type 2
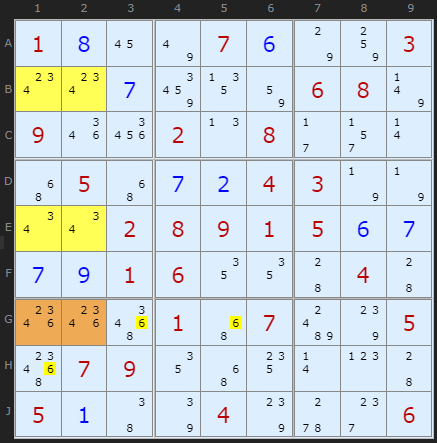
We can look in both the row and the column for the Roof cells (orange). We need to find two more cells that are in a different box and have exactly one extra candidate in both. In the example our Deadly Rectangle triple is {2/3/4}. The extra candidate in G23 is 6. The logic is that 6 must appear in either of G2 OR G3 since without it a deadly Rectangle on {2/3/4} would be created. Knowing this allows us to remove all 6s in the row and box.
If the orientation of the Type 2 was the other way round we'd eliminate in the box and column.
Many thanks to prompts in the comments below and to Ross Trusler for the example he found in the first puzzle in the Fireworks strategy. Turn off Fireworks to get it to show.
Type 4
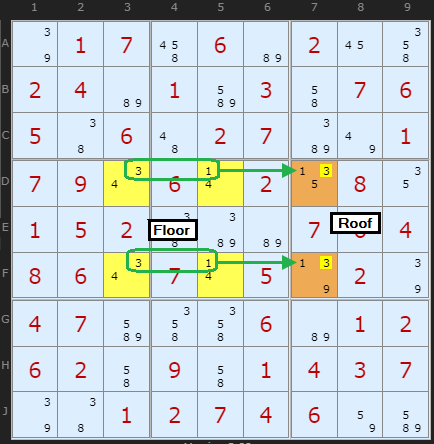
Instead of a single locked pair of cells we can have two - if they are in different boxes and the roof is in a different box as well.
To see this example you do need to turn off the Tough and XY Chain strategies so the solver can find it. The double Locked Pairs on DF35 (locked by the 4's) which effectively solve to a 1/3 Locked Pair, which then become a UR Type 4 with D7/F7 locked by the 1's, eliminating the 3's. You can see there are no other 1s in column 7 or box 6.
I will admit, instances of the Extended Unique Rectangle are not common, but if you are just getting into Unique Rectangle you'll be looking for the very common Type 1. I think it's worth keeping an eye out for this formation at the same time. You will notice a similar cluster of common candidates and it's just possible - if you remember the three boxes spread rule - that you'll find one when you're looking for the 2 by 2 version.
Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Pieter, Newtown, Oz
Assuming the "12" pairs are Naked Pairs (no other candidates), this is virtually a "stretched" Type 1 UR.
Also @Andrew
I refer you to Jonathan Handojo's comment on 2021-06-9 finding that the Solver skips UR's and jumps to WXYZ, similar to my earlier comment on 2019-12-16.
I also found a sorta Type 5 in your daily puzzle for 2023-01-21 but not in the Solver order, which I will try to retrieve and send separately.
As always thanks for a fabulous website!
Ciao, Pieter
... by: Anonymous
Hidden EURs too.
... by: Anonymous
... by: Pieter, Newtown, Oz
I believe I have found an Extended UR in your Daily Sudoku for 2022-05-7, not a 2x3, but a 3x2. After solving the basics (and turning various strategies off?) one can arrive at this board (as I did on paper):
bd=800000251001507830053812607145936782730285410008174503314628975080751300500000108
The EUR is in AJ456, however, the solver does not find it, I think cuz you haven't implemented this variety yet?
Also, I noticed several of my and others' earlier comments which you may not have seen or replied to yet.
Thanks and kudos as always!
Ciao, Pieter
... by: Travi
Apologies if I'm repeating something that's already known (I'm fairly new to sudoku), but there's an additional way to extend the principle of unique rectangles. Unfortunately, I don't have an example handy, but consider the following:
In column 1, we have a 1-2 pair in boxes A1 and D1.
In column 2, we have a 1-2 pair in boxes A2 and E2.
In column 4, we have a 1-2 pair in boxes D4 and E4.
I'm calling this a "crooked" rectangle, and it's another deadly pattern. Of course the 'rectangle' can bend in this fashion more than once, but as long as the bends eventually line up with a pair in the same row/column at both ends it's a deadly pattern.
Aaaand scrolling down I just saw Brett Yarberry describing exactly this phenomenon. Guess I'm several years late to the party.
... by: Pieter, Newtown, Oz
As always thanks for a fabulous website! I have learned so much about Sudoku from your site.
Solving your Daily Sudoku for 2020-02-1 I believe it has multiple HURs and an Extended UR which the solver does not find.
After solving the basics, and turning Tough strategies off, the solver (V2.08) skips all URs to a WXYZ Wing.
I have commented separately on the HURs.
The EUR is, I believe, a Type 1 in AFJ89. Using Swordfish terminology, I see it as a 2-2-2 EUR. I also see EURs as overlapping URs similarly to how you do.
For this example, my picture is this:
- The double conjugate pairs of 7s in FJ89 reduces the locked pairs of 1/7 in F8/F9, and 5/7 in J8/J9, to a virtual locked pair of 1/5s.
- the virtual 1/5 locked pair in FJ89 combines with the 1/5 in A8 to form a Type 1 UR, eliminating the 1 and the 5 from A9.
Is this correct?
Ciao, Pieter
The solver can (now) find this example if the tough strategies and XY-Chain are turned off
... by: Pieter, Newtown, Oz
I believe I've found an example of an EUR Type 4, but when I plugged it in to the solver I was disappointed that the solver didn't find it. 🙠Then I read that you have only implemented EUR Type 1 (though you call it simply a UR, not an EUR. Clarification?).
In your reply to Ian below (2014-06-12) you mention that you "picture that the EUR is composed of several overlapping URs". This one is exactly that - two 2x2 URs - and I also think I have seen this structure before.
The original puzzle is:
bd=007060200040103070500000001090602080100000004060705020400000002020901030001070600
which solves to
bd=017060200240103076506027001790602080152000764860705020470006012620901437001274600
At this point, if you turn off the Tough and earlier Diabolical strategies the solver will find the Hidden UR on EG45, but not the EUR on DF357. Easily spotted is the double Locked Pairs on DF35 (locked by the 4's) which effectively solve to a 1/3 Locked Pair, which then become a UR Type 4 with D7/F7 locked by the 1's, eliminating the 3's.
Personally I have no trouble detecting UR's types 1-4 but honestly I just can't get my head around 2b, 2c, 3b! When you're familiar with UR's in general I find they tend to stick out like dog's balls parallel to locked pairs, and I often find them even before I've checked for X-Wings, etc! Surely an EUR Type 4 can't be too difficult to program?
Always love perusing your website!
Thanks!
Pieter 🙂
... by: Pieter, Newtown, Australia
Firstly Congratulations on your Solver's 10 year anniversary which I just noticed is TODAY, 28th of May!'' An amazing milestone!!!
I was completing the diabolical sudoku on an old printout of your Daily Sudoku for 26/9/2014 when I happened to notice an EUR (which I was not previously familiar with). You mention they are not very common so I thought I'd point it out. You need to turn XY chains and 3DM off for the solver to find it.
Thanks as always for your great website.
Here's to the next 10 years!!! ;-) :-D
Ciao
Pieter :-)
... by: Brett Yarberry
Besides the standard 2x2 pattern and the 2x3 pattern, there are:
A . . | B . . | . . .
B . . | . . . | A . .
. . . | A . . | B . .
A . . | B . . | . . .
B . . | C . . | . . .
C . . | A . . | . . .
. A . | B . .| . . .
B . . | A . . | . . .
. . . | . . . | . . .
~ ~ ~ ~ ~ ~ ~ ~ ~
B A . | . . . | . . .
. . . | . . . | . . .
. . . | . . . | . . .
There are even more complex patterns, but I hope these simple ones could be useful.
... by: Ian
Been trying to see what additional benefit the extended UR brings to the solution over the regular one and I have to confess that I can't actually see any. Is not an extended UR just a regular UR with a locked set and intersections between the locking doublet and the 'roof' cells?
Allow me to elucidate... In your top extended UR; Let E13 and G13 be a regular UR on 13 and 35 respectively and, as a consequence, let C3 be a doublet locking rows E and G together. This, effectively, makes E3 and G3 'floor' cells implying that E1 and G1 may be considered 'roof' cells. Since C1 subtends both roof cells and the locking doublet, is this not a bog-standard Type 3 Regular UR? I would continue to argue the case that all extended UR's are special (or specific) cases of 1 or more generic regular UR's. If I am misisng something, please would you point it out for me. I'd be very grateful. Absolutely brilliant site and thank you for your excellent insights. Cheers! Ian
... by: Mark
In your Extended Unique Rectangles, example one where you have {1,3,5} as the main entries which might cause a deadly pattern if it was not for the presence of the extra candidate 6, I have gone through it several times, and I have NOT found a deadly pattern. Would you please kindly respond to my email and tell me where I am wrong. I spent too much time on it, and I know you are a very busy person; however, I would greatly appreciate if you respond.
Note: I can easily see the deadly pattern in example 2 and 3.
Best regards,
Mark
All three examples are pretty close in pattern. Do you agree that in the first example if the 6 wasn't there then all the colored cells would contain only 1, 3 and 5? Some cells are missing one of the numbers which cuts down the number of combinations that could complete those cells, but not down to one, so it's a multiple solution without the 6.
Just the first two I can think of staring at the cells:
1 - 5
3 - 1
5 - 3
5 - 1
1 - 3
3 - 5
Hope that helps a bit
... by: RenStimpy
I believe example 3 proves this theory to be incorrect. Unless I misunderstand what you're saying, the 38 pair on E2 and the 37 pairs on column 6 would imply that 7 & 8 are the only choices for the two cells in column 7. However, J7 eventually evaluates to be 7, meaning you really only had a choice between 3 and 8 for three of the cells in the extended UR.
To Andrew,
Great website! If I had an extra arm I'd give you three thumbs up!
... by: bcorso
Regarding my previous post. I've come to the conclusion that the only deadly pattern available for a 3x2 extended UR is of the form
xy | xy
xz | xz
yz | yz
That is, to get a 3 x 2 deadly pattern each row must only contain 2 candidates, those 2 candidates must be the same for each row, and those 2 candidates can not be the same for any column. This leaves only permutations of the above patterns as possible deadly patterns.
Proof:
First off, each cell MUST only contain two candidates AND those two candidates MUST be the same for both deadly cells in that row. This is because a deadly pattern means that if ALL other cells are filled in on the board, there still exists multiple solutions. Thus, if all other cells in the rows are filled in, there are only two candidates that can be placed in the deadly cells of that row, and those candidates are the same for both of the cells.
Second, the pairs in the columns cannot be the same. This follows from the fact that if there were two pairs that matched, there would no solution (instead of multiple solutions). For example, if xz was repeated twice in the column:
xy | xy
xz | xz
xz | xz
Then there would be no solution because the second and third column would have to have the same solution, which is impossible.
... by: bcorso
Please let me know if I am missing something important, but I see a flaw in the extended URs that you present here.
The way I understand it, a deadly solution only exists if the candidates in the "deadly" cells cannot see any other cell with those candidates (because the deadly cells cannot solve themselves, thus they need other cells to make further eliminations).
For example, in the 2x2 deadly URs it is deadly because the 4 cells contain a naked pair in the row, col, and box and the "naked pair" technique will remove those candidates from every cell those deadly cells can see. Thus, the naked pairs have multiple solutions because they cannot solve themselves.
Now, in the extended URs I image you would need the same circumstance, the deadly cells cannot see any other cells with their candidates, otherwise that cell can be used to break the deadly pattern. This brings me to your examples here. In both examples you only require a triple in the row OR col. but this obviously leaves cells (outside the deadly cells) with the same candidates which are in the same box and col OR row respectively.
I'm interested in hearing your solution, thanks Andrew.
... by: Dale Kloss
First the two Extended Deadly pattern solutions:
1 5 5 1
3 1 1 3
5 3 3 5
I don't see a problem with these as horizontally the 2 solutions are deadly, the patterns are deadly inside the 3 boxes, and they are deadly vertically. Since we are told the solution to the entire puzzle is unique they can be eliminated as possible solutions.
Now let's tabulate the other two possible solutions:
Pattern A: 1 5 Pattern B: 6 | (1,5)
5 3 (1,3,5) | (1,5)
3 1 (1,3,5) | (1,3,5)
This is where I have the problem. I don't see Pattern A as Deadly with respect to row E of the first two solutions nor Deadly with respect to row G of the first two solutions since the candidate sets are different. Nor is it Deadly with respect to Boxes 4 and 7 since the candidate sets are different.
Conclusion ? Either Pattern A or B destroys the Deadly pattern. We can't say that just the 6 destroys the pattern ?
One bright spot: By comparing Patterns A and B we see that we can eliminate the 5 in cell C1.
Let's call the first two patterns you described as C and D as they are unnamed.
Pattern B is not deadly because it's actually going to be the solution, ie 6 in C1 and some combination of the other candidates in the other cells which will come out in the wash later.
Pattern A is deadly with both C and D. Now, A with C doesn't look swappable in isolation because they both share 1 and 5 in C1 and C3. But they do swap candidates in cells E1,E3 and G1,G3. So in isolation just thinking about A and C we are effectively using four cells out of 6 to prove a point which seems insufficient because C1 and C3 are not being swapped. However, the super-set pattern AC can be swapped with pattern D. So we have three patterns which in combination can create swappable cells. This is the neat thing about triples - we don't need every candidate to be swappable in all cells, just as long as each cell and each candidate can be swapped in at least one combination.
Another way to think about it: It would be easier to show the total swapability of all patterns if we had a 1,3 and 5 in all six cells. The fact we are missing a 3 in C1 and C3 and a 5 in E3 merely restricts the number of swappable patterns available to patterns A, C and D. The minimum number of swappable patterns is two and we would get that in slightly more rare situations where all cells contained 2 candidates (apart from the extra one candidate) similar to the second example.
... by: Ehsan Vessal