Hidden Unique Rectangles
All the Unique Rectangles discussed on this page have had at least two bi-value cells (or a Naked Pair, if you like). An interesting situation emerges when we have only one bi-value cell and the Unique Rectangle is buried, or 'hidden', under lots of other candidates. The conditions have to be just right, but this formation is surprisingly common.
Update Sept 2025: New examples have been sourced that the solver will find without unchecking other strategies and the solver will now display the Strong Links.
Update Sept 2025: New examples have been sourced that the solver will find without unchecking other strategies and the solver will now display the Strong Links.
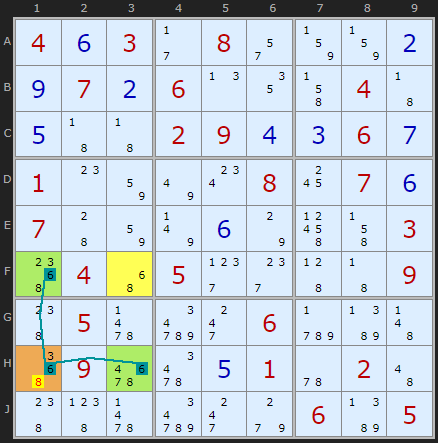
The types of Unique Rectangles that we've examined so far simply won't work here. However, all is not lost because something interesting is going on in the corner opposite to F3. 6 in H1 is part of two strong links in the row and column - that is, 6 occurs only twice in row H and column 1. Our 6 in this rectangle can have only one of two possibilities.
Looking at H1, lets make "Option A" the case where H1 is 6. The pairs or "strong links" remove 6 from F1 and H3. Option B is where H1 is not a 6. That would put a 6 in F1 and H3.
Let us conjecture that the solution to H1 is 8. That forces the 6s to take on option B because they would be the only remaining 6s in that row and column (F1 and H3). The implication of this option is that the only candidate for F3 is 8. But, wait a moment - this is exactly the deadly pattern we need to avoid - two numbers in two rows, two columns and two boxes. Since none of these cells is a clue, the puzzle could have two solutions. We can swap the 6 and the 8 around. This makes option B unviable.
So surely we can fix the 6s in F1 and H3? Not quite. We haven't taken into account the clutter of other clues in the corners of this rectangle. But we can say something about the 8 in H1. We've excluded it for the reason above, but option A also excludes the 8 in H1. Whichever way round F1 is, H1 cannot contain a 8, so we can remove it from that cell.
So surely we can fix the 6s in F1 and H3? Not quite. We haven't taken into account the clutter of other clues in the corners of this rectangle. But we can say something about the 8 in H1. We've excluded it for the reason above, but option A also excludes the 8 in H1. Whichever way round F1 is, H1 cannot contain a 8, so we can remove it from that cell.
Type 2 Hidden Unique Rectangles
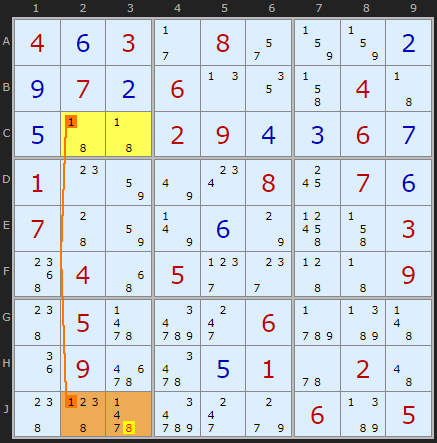
In Figure 2, the cells C2, C3, J2 and J3 (also known as CJ23) form a rectangle with a potential deadly pattern on [1/8]. In type 2 we have an identifiable Floor consisting of C23 — both bi-value cells. And the Roof contains a clutter of other candidates. We still want to avoid reducing this rectangle to 1/8 in all four cells.
Type 2 starts with a Naked Pair, 1/8, and we're checking for which strong links exist on the pair candidates. The Naked Pair is obviously a double strong link on both numbers, but candidate 1 has a strong link to the Roof in column 2. From this we can start using the logic of Type 1.
Is 8 viable for either Roof Cells? J2 is viable since J3 does not have to be 1. However, J3 as 8 is trouble because it forces C3 to be 1, C2 to be 8 and because of the strong link, J2 becomes 1. A Deadly Pattern. So it is safe to remove 8 from J3. At first glance the formation looks symmetrical but its the other 1s and 8s (or lack of) in the columns that give us the implications of the Hidden Rectangle.
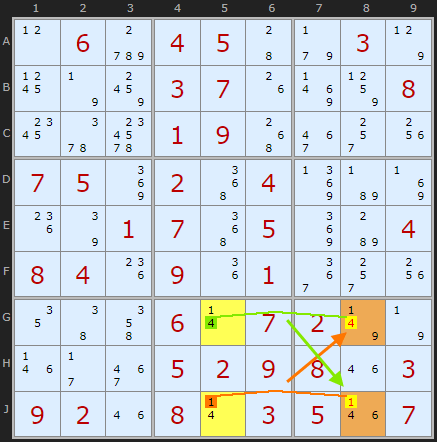
Up to 2024 I was a little too restrictive with the pattern - particularly if there are two strong links operaing on two candidates at the same time allowing two eliminations. Thanks to David Hollenberg for this example.
Hidden Unique Rectangle
Type 2: removing 4 at G8 because of GJ58 and one strong link on 1 between J5 and J8
Type 2: removing 1 at J8 because of GJ58 and one strong link on 4 between G5 and G8
Type 2b Hidden Unique Rectangles
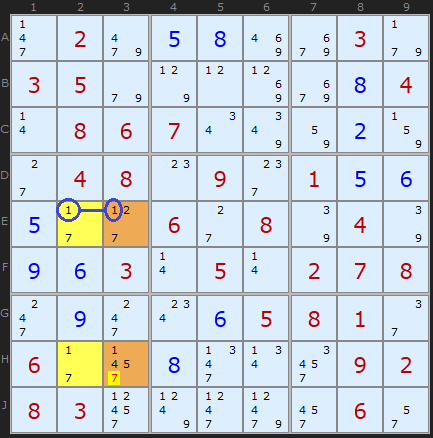
The yellow cells are the floor with conjugate pairs 1/7. The Deadly Rectangle extends to E3 and H3 (orange) where 1 and 7 are also present among other candidates. The strong link on 1 between E2 and E3 means that a 7 in H3 would create a Deadly Rectangle.
Thanks to Jerry Foil of Virginia, USA for providing the first example. Interestingly this type of Hidden Unique Rectangle is almost twice as common as the Type 1 and three times as common as Type 2.
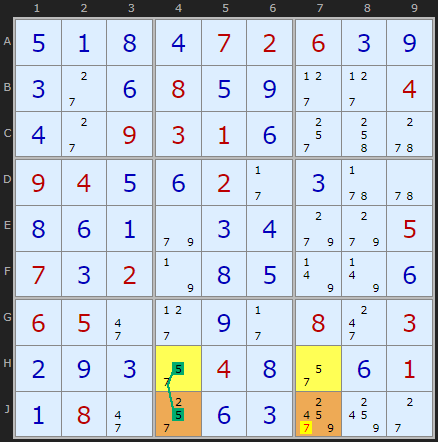
Klaus Brenner in Germany has created some very beautiful Sudokus like the one on the right. It solves trivially up to the point where a Type 1, Type 2 and Type 2b are used consecutively. In the screen shot the Type 2B is shown with the floor in row H.
HIDDEN UNIQUE RECTANGLE Type 2b: removing 7 at J7 because of HJ47 and one strong link between H4 and J4 on 5
Note: Uncheck XY-Chains to find these HURs

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Visitor
There is a strong link also from 8 in H3 to 8 in F1.
If H3 was 8, then F1 becomes 8, and this puts 6 in F3 and H1 - a deadly pattern!
In my opinion, 8 in H3 should therefore be highlighted in yellow also since it can be removed.
+8[H3]-8[GHJ1]
-8[GHJ1]+8[F1]
+8[F1]+6[F3H1]
deadly pattern
8 to be removed from H3
I can see the pattern but on its own it still leaves a 3 in H1 so no deadly pattern. But if it is paired simultaneously with the existing UR then +6[H1] removes that 3. Convoluted but logical.
... by: Anibal
Why would that be a deadly pattern? Setting a 6 in resolves all cells. No 6/8 deadly pattern is found so I'm not following the example.
Do you mind clarifying, please?
Best regards,
A.
Now if a solution is found continuing from this point, it will imply the existence of another solution with all the digits the exact same except for DF37 having the 6s and 8s swapped around.
This cannot occur as there should only be one solution to the puzzle, so 6/8 cannot be true in DF37, thus 6 cannot be true in D3.
... by: Rick
I sometimes use a variant of hidden unique rectangles which I call reversed unique rectangles.
On some difficult puzzles it often appears that there are three parts of a hidden unique rectangle but the fourth corner does not include the magic to candidates. by adding back previously eliminated candidates into the cell one can create a hidden unique rectangle again and then apply the logic of that to eliminate candidates in other three cells.
... by: Atari4600
This is from Daily Sudoku #5953 (Dated April 19, 2024)
I discovered a hidden unique rectangle that the Sudoku Solver did not pick up. (i.e. the next step should pick up the hidden unique rectangle BEFORE AIC).
When this is loaded in the solver, continue to take steps until you reach Step #13 when it introduces an AIC. Go back (<<).
The four cells that make up the Unique Rectangle is E7, E8, G7, and G8. Be aware that either E7 or E8 must contain a 1. And either G7 or E7 must contain a 1.
and look at Cell G7 (Which has candidates {1, 2, 5, 7})
We must ask ourselves the questions, whether G7 may be a 1?
If G7 is a 1, G8 must be a 5 (hidden single), E7 must be a 5 (hidden single), and because E7 may not be a 1 (Because of G7), that leaves E8 to be a 1 (Naked Single).
As you can see:
E7 = 5, E8 = 1
G7 = 1, G8 = 5
Which is a deadly pattern. Therefore, the 1 may safely be removed from G7.
I would appreciate it if you could look into this and let me know your thoughts!
Very truly yours,
Atari4600
... by: FredOnCyc
Your example 1 for HUR.
If enabled HUR only, your solver stops.
But maybe there is a HUR (type 2) at HI34 which removes 8 from H4?
Regards
... by: Jonathan Handojo
... by: Jonathan Handojo
.......75...3.1.4..6...2.9.....8.3...7.....8...374.....4.....2..1.6.8...93.2.....
If you use the Solve Path with every checkbox ticked, you get a WXYZ-Wing evaluation. It seems to have skipped through the Unique Rectangles strategy when there's one in B7, B9, J7 and J9 that allows the eliminations: 8 from J7, 6 from J9, and 8 from B9. Either value you force into them forms the deadly pattern, so I solved the puzzle quite with ease after using this. Now I'm not too sure of the rules with this, but I only saw it through forcing.
... by: Pieter, Newtown, Oz
As always thanks for a fabulous website! I have learned so much about Sudoku from your site.
Solving your Daily Sudoku for 2020-02-1 I believe it has multiple HURs (and an Extended UR) which the solver does not find.
After solving the basics, and turning Tough strategies off, the solver skips all URs to a WXYZ Wing.
However, I believe there is a double Type 2 HUR in AB16, with the floor in A6/B6 (5/7) and a conjugate pair of 7's in A1/A6 eliminating the 5 in B1, and a conjugate pair of 7's in B1/B6, eliminating the 5 in A1.
The second HUR is a Type 2 HUR in EJ46, with the floor in E4/E6 (3/4) and a conjugate pair of 3's in E6/J6, eliminating the 4 in J4.
The third HUR is a Type 1 HUR in HJ16, with a bivalue 2/8 in H6 and a (double) conjugate pair of 8's in H1/H6, eliminating the 2 in J1.
The Extended UR is in AFJ89 which I have commented on separately under XURs.
Is this correct?
Ciao, Pieter
... by: Pieter, Newtown, Australia
As always thanks for a fabulous website!
Solving your Daily Sudoku for 2019-09-28 I believe it has some Type 2b HUR's which the solver does not find.
After solving the basics, a UR, a 3DM, and a HUR, we are left with this board.
The solver then skips to an AIC, but I believe there is a HUR Type 2b (a double in fact) in HJ17.
The floor is a 7/8 pair in J1/J7.
The first HUR eliminates the 7 in H1 due to the strong link of 8's in H7/J7.
The second HUR eliminates the 8 in H7 due to the strong link of 7's in H1/J1.
Is this correct?
Ciao, Pieter
... by: Pieter, Newtown, Australia
Noticed you don't actually have a heading for "Type 1".
Thanks for a brilliant and educational website, as always. Recommended it to a friend just tonight!
Ciao, Pieter
... by: jaswant singh
... by: Hassieb
In example one there is also 6 in D7 that could be removed as well because we can make exactly the same argument as we did for the 6 in D3 unless I do not see something.
Regards,
Hassieb
... by: Sheela Ravishankar
Also I have started appreciating the AIC technique better after reading your website. In fact I can solve almost all your Diabolic and Extreme Sudokus now.
Thanks for the good work and great help!!!
... by: J.S.SRAN sriganganagar INDIA
... by: Joris Engels
... by: Hassieb
... by: TAU
... by: Jools
Further to Sean's post, I've also found [at least] two examples of such a "diagonal" hidden non-unique rectangle that could be added to your solver. Both examples satisfy the existing NUR rules. You should be able to step through both grids in the solver until coming across an XY-wing, when they should become visible.
1st example
Type (i) 5/8 in F1 and G3; entering a 5 in F3 would force G1 to become one too - thus forming a "deadly" pattern, so the 5 in F3 can be removed.
Doing this enabled me to breeze through the rest of the puzzle (after also completing the XY-wing on C2-H2-G3 which removed the 5s in B3 and C3), because it immediately left just a single 5 in G3 for column 3.
Note that type (i) candidates do not have to form part of a N=2x2 pattern.
2nd example
This one actually has two types at once; the second removes two candidates!
Type (i) 2/6 in D7 and F5; entering a 2 in F7 would force D5 to become one too - thus forming a "deadly" pattern, so the 2 in F7 can be removed.
Type (ii) 6/7 in G6 and H9; entering a 7 in either G9 or H6 would force the other to be the same - again forming a "deadly" pattern, so both 7s in G9 and H6 can be removed.
Note that type (ii) candidates *do* form a N=2x2 pattern, which enables both corners to have a candidate removed.
Both examples come from my Nintendo DS Platinum Sudoku cartridge, from the 5,000,000 grids on "Pro" level. (I'm up to #3293 so far!)
... by: Sean Tremba
I think I've come up with a variant on unique rectangles that doesn't seem to be covered by any of your HUR or UR strategy types. (You can certainly correct me if I'm wrong).
Suppose you have an "x-wing" formation on a given candidate, and you have identical bi-value cells diagonally opposed to each other in that formation. That is, you have two cells with xy as candidates at diagonal corners. The other two cells then must contain x with some other set of candidates (which may or may not include y). I maintain that you can then conclude that x is the solution to the two diagonal cells which have xy as candidates.
To prove this, assume that x is not the solution to these diagonally opposed cells. x is therefore solution to the other two cells in the "x wing" formation. Since the only other candidate for these cells is y, y must then be their solution. However, this leads to a deadly pattern, since you have a rectangle with y as the solution to the cells on one diagonal and x as the solution on the other; x and y could be reversed to give a second valid solution.
More concretely, (and also the example I found), suppose cells F1 and H2 are bivalue cells with 7 and 9 as candidates. In the sudoku I was working, cell F2 had candidates 1,7 and 9, and cell H1 had candidates 7,8 and 9. These cells were the only cells on rows F and H which contained 7's, and the only cells in columns 1 and 2 which contained 7's. The solution to cells F1 and H2 must then be 7. Otherwise, the solution to F1 and H2 would be 9, and the solution to F2 and H1 would be 7, which creates a deadly pattern.
... by: Chuck Bruno - Virginia
Load puzzle
Thanks,
Chuck Bruno
... by: John