SudokuWiki.org
Strategies for Popular Number Puzzles
X-Wing Strategy
This strategy is looking at single numbers in rows and columns. It should be easier to spot in a game as we can concentrate on just one number at a time.
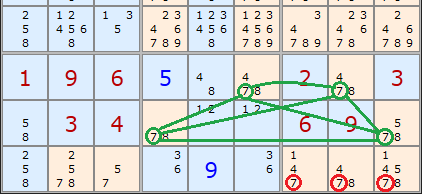
Well, A and B are a locked pair of 7s. So are C and D. They are locked because they are the only 7s in rows B and F. We know therefore that if A turns out to be a 7 then B cannot be a 7, and vice versa. Likewise if C turns out to be a 7 then D cannot be, and vice versa.
What is interesting is the 7s present elsewhere in the fourth and eighth columns. These have been highlighted with green boxes.
Think about the example this way. A, B, C and D form a rectangle. If A turns out to be a 7 then it rules out a 7 at C as well as B. Because A and CD are 'locked' then D must be a 7 if A is. Or vice versa. So a 7 MUST be present at AD or BC. If this is the case then any other 7s along the edge of our rectangle are redundant. We can remove the 7s marked in the green squares.
The rule is
When there are
The reverse is also true for 2 columns with 2 common rows. Since this strategy works in the other direction as well, we will look at an example next.
The rule is
When there are
- only two possible cells for a value in each of two different rows,
- and these candidates lie also in the same columns, then all other candidates for this value in the columns can be eliminated.
The reverse is also true for 2 columns with 2 common rows. Since this strategy works in the other direction as well, we will look at an example next.
In this second example I've chosen a Sudoku puzzle where an enormous number of candidates can be removed using two X-Wings. The first is a '2-Wing'. The orange high lighted cells show the X-Wing formation. Note that the orientation is in the columns this time, as opposed to rows as above. Looking at columns we can see that candidate 2 only occurs twice - in the orange cells. Which ever way the 2s could be placed (E5/J8 or E8/J5) six other 2s in the rows can be removed - the yellow highlighted numbers.
A few steps later the second X-Wing is found on candidate 3 in the same rows. Whichever way round the 3 can be placed in those rows (E2/J8 or E8/J2) there can be no other 3 in rows E and J except in those orange cells.
Generalising X-Wing
X-Wing is not restricted to rows and columns. We can also extend the idea to boxes as well.
If we generalise the rule above we get:
When there are
then all other candidates for that value can be eliminated from the latter two units.
Now we have 6 combinations:
If we generalise the rule above we get:
When there are
- only 2 candidates for a value, in each of 2 different units of the same kind,
- and these candidates lie also on 2 other units of the same kind,
then all other candidates for that value can be eliminated from the latter two units.
Now we have 6 combinations:
|
|
Here is an example of combination 5. Starting from 2 rows and eliminating in 2 boxes, in this case the last two boxes in the Sudoku. The rows are 7 and 8 and they each have two 7s. Our x-Wing is now a trapezoid but the logic is the same. We can be certain that 7 can be eliminated in the red circled cells.
But HOLD UP one moment. There is a simpler strategy that does the same job!
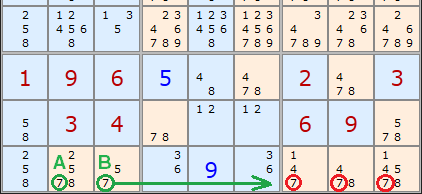
A and B above are a pointing pair. This removes the same 7s in the same place. Combination 6 is also the complement of a pointing pair. Combinations 3 and 4 are also complements of the Line/Box Reduction. Our generalisation of X-Wing to boxes hasn't profited us at all. We learn that
X-Wings containing boxes are the inverse of the Intersection Removal strategies
But HOLD UP one moment. There is a simpler strategy that does the same job!
A and B above are a pointing pair. This removes the same 7s in the same place. Combination 6 is also the complement of a pointing pair. Combinations 3 and 4 are also complements of the Line/Box Reduction. Our generalisation of X-Wing to boxes hasn't profited us at all. We learn that
X-Wing Exemplars
These puzzles require the X-Wing strategy at some point but are otherwise trivial.They make good practice puzzles.
- Exemplar 1, x1 (score 80)
- Exemplar 2, x1 (score 82)
- Exemplar 3, x2 (score 174, +1 Naked Pair)
- Exemplar 4, x2 (score 178, +1 Naked Pair)
Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: paul
you suggested an Xwing in a step to the solution of my sudoku.
the 3 was identified...
D2 [2,3,8] - D7 [2,3,5,8]
H2 [3,5,8] - H7 [3,5,8]
however the 3 was also on line J and made the X as well...
J2 [2,3,5,8] - J7 [3,4,5,8,9]
why did you choose line H instead of line J?
I can send a pic to you if you want clarification. Just email me.
cheers
... by: Aleksandar
Did Exemplar 2, x1 (score 82) in a few minutes and I didn't spot any X-wing there. It simply resolved 1 by 1
Can you spot it on this step?
Thank you for the attention :)
... by: Digdoug
In paragraphs four and five, it says that the candidates which can be eliminated are highlighted in green, but they're actually highlighted in yellow - the green ones are the 7s in the orange boxes which make up the x-wing.
... by: fred
in this case 7 is also in j5 j6 j7.
... by: Rodney Lindenmayer
... by: Ymiros
... by: kauaikarl
... by: hawkeye
since a multiplicity of examples helped me to understand !
I am embarrassed that I didn't catch on before.
... by: Hexameron
... by: Marja Glas
... by: Jim Birch
... by: Thurstan
... by: Tom
In response to David Spector: because the trial-and-error method of solving sudokus isn't so interesting. Somewhere on Andrew's site he says this: his interest is in the logic, not the brute force methodologies. I've done diabolical and extreme sudokus using the "try-one-number-in-a-cell-with-two-remaining-possibilities-and-if-it-doesn't-work-try-the-other-one" technique (targeted trial-and-error), and whilst it gets the solution I'm left dissatisfied, thinking how did that work?
... by: Jayaprakash
... by: Riddlemethisbatman
... by: Vinod K Chandran
Thanks for this page. Its really very helpful.
... by: David Spector
This is so much simpler than all those advanced strategies, so complex, which may or may not apply.
... by: Bill
... by: Bill
... by: JuanBeegAhs
Looking at the other examples just seems to reinforce this haze for me. It doesn't seem like there has to be a fixed number of squares between or anything, as long as four similar numbers can be in a square or even trapezoid apparently.
... by: gcrupa
(Row->Col) 7 taken off D1, based on DH29
(Row->Col) 7 taken off H1, based on DH29
(Row->Col) 7 taken off H8, based on DH29
I do not know what DH29 stands for and also did not know where to look for it.
Can you tell me, please ?
Have a nice day
gcrupa
... by: June K
... by: Simon Davitt
Please can you give some un-worked samples for each page to allow people to test their understanding.
... by: Richard
... by: fdan
... by: Lydia
... by: sajan
Thanks
Sajan
... by: Trophy
Now, people do come up with logical methods and it's usually by combining several ideas in one go. This is the coal face I'm picking at now, trying to generalise these ideas and get them into code.
However, it will be a rare puzzle in the newspapers that can't be solved logically. We really have to search for a long time to find unsolvables (currently they are 1/10,000) from my generator.
Computers can't mimic inspiration and there's still a place for that in Sudoku, if you get stuck
... by: Daran
... by: Complex sudoku newbie
... by: M Bakhtian
... by: RLets
... by: Dino Hsu
... by: Konrad M Kritzinger
... by: Konrad M Kritzinger
... by: Yves Sioui
... by: Ted L
A wonderful site which gives great pleasure and instruction - thank you very much.
... by: William Mann
... by: Harold Binley
H
... by: Rohan
1. No occurrence of the number (in this case 6) can occur in the rows between A and B or C and D;
2. the classic X-Wing uses only the extreme boxes at the edges of the puzzle since otherwise, as Colin Pierce pointed out why could one not use the blue boxes above C and D? Because if one did there would be a very different result.
Whatever, thanks for your very useful site, it has helped me greatly!
... by: Elmer Schartow
I'm being picky but the second para after the first illus points out the boxes BETWEEN AB and CD which are highlighted in yellow. On my computer the boxes ABCD themselves are yellow and the boxes BETWEEN ABCD are highlighted in cyan.
I believe the first question posed by colin pearce is a valid one and needs to be answered. Also the situation regarding the 7 in cell X posed by CS Vidyasager appears to be completely valid IF there are no 7's in A and B.
... by: colin pearce
thank you for this extraordinary and marvellous site.
I have a question on your X-wing principle. The top diagram with the yellow boxes ABCD... (and I hope I;m not being obtuse here), but why couldn't the four yellow boxes include, instead of C and D, the two blue boxes above them, this eliminating C and D as options?
Thanks again.. I love this resource,
cheers
colin
... by: Marv Rowe
... by: CS Vidyasagar
thanks
... by: Kantilal M Mane
... by: John Mathews
... by: Faris
... by: Nick Pannell