 |
 |
| Print Version |  |
| Solvers |
| Puzzles |
| Basic Strategies |
| Tough Strategies |
| Diabolical Strategies |
| Extreme Strategies |
| Depreciated Strategies |
| Str8ts |
| Other |
|
 Order Now! |
 Order Now! |
This is an extension of Y-Wing or (XY-Wing). John MacLeod defines one as "three cells that contain only 3 different numbers between them, but which fall outside the confines of one row/column/box, with one of the cells (the 'apex' or 'hinge') being able to see the other two; those other two having only one number in common; and the apex having all three numbers as candidates."
It follows therefore that one or other of the three cells must contain the common number; and hence any extraneous cell (there can only be two of them!) that "sees" all three cells of the Extended Trio cannot have that number as its true value.
It gets its name from the three numbers X, Y and Z that are required in the hinge. The outer cells in the formation will be XZ and YZ, Z being the common number. |
 XYZ-Wing theory |
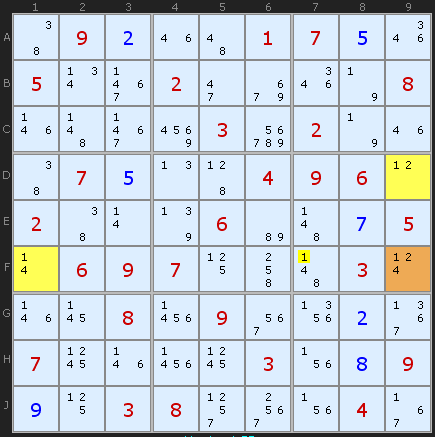
In this example the candidate number is 1 and F9 is the Hinge. It can see a 1/2 in D9 and a 1/4 in F1. We can reason this way: If D9 contains a 2 then F1 and F9 become a naked pair of 1/4 - and the naked pair rule applies. Same with F1. If that's a 4 then D9 and F9 become a naked pair of 1/2 each. If any of the three are 1 then 1 is still part of the formation. Any 1 visible to all three cells must be removed, in this case in F7. |
 XYZ-Wing example 1: Load Example or : From the Start |
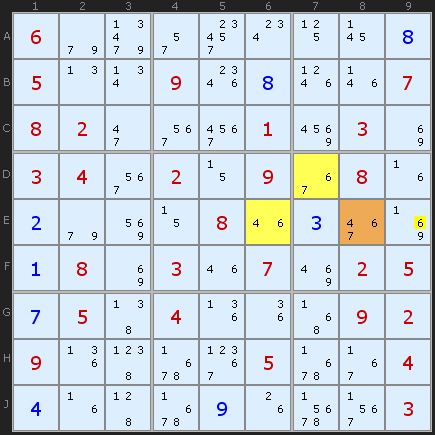
| The second example shows an XYZ-Wings based on a row and a box. The hinge cell is on E8 and the common candidate is 6. The 6 in E9 can see all the 6s in the whole XYZ formation. Aligned Pair Exclusion The logic on an XYZ-Wing is completely different and lot simpler than the Aligned Pair Exclusion described below but the funny thing is that XYZ-Wing is a total sub-set of APE. Every XYZ-Wing can be solved by APE (but not vis versa). |
 XYZ-Wing example 2: Load Example or : From the Start |