Main Page - Back
 
XYZ-Wing
From sudokuwiki.com, the puzzle solver's site
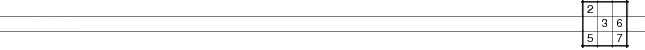
breakline
This is an extension of Y-Wing or (XY-Wing). John MacLeod defines one as "three cells that contain only 3 different numbers between them, but which fall outside the confines of one row/column/box, with one of the cells (the 'apex' or 'hinge') being able to see the other two; those other two having only one number in common; and the apex having all three numbers as candidates."

It follows therefore that one or other of the three cells must contain the common number; and hence any extraneous cell (there can only be two of them!) that "sees" all three cells of the Extended Trio cannot have that number as its true value.
It gets its name from the three numbers X, Y and Z that are required in the hinge. The outer cells in the formation will be XZ and YZ, Z being the common number.
 XYZ-Wing eg 1
XYZ-Wing eg 1
In this example the candidate number is 7 and R3C5 is the Hinge. It can see a 1/7 in R2C4 and a 5/7 in R3C8. We can reason this way: If R2C4 contains a 1 then R3C5 and R3C8 become a naked pair of 5/7 - and the naked pair rule applies. Same with R3C8. If that's a 5 then R2C4 and R3C5 become a naked pair of 1/7 each. If any of the three are 7 then 7 is still part of the formation. Any 7 visible to all three cells must be removed, in this case in R3C6.

(Note: Turn OFF Y-Wings and Unique Rectangles) 		XYZ-Wing eg 1
XYZ-Wing eg 1: Load Example
The second example shows a two XYZ-Wings with a few steps in between. R4C6 is happens to be common to both XYZ-Wings and the candidate in question, number 7, is also common to both.

Aligned Pair Exclusion

The logic on an XYZ-Wing is completely different and lot simpler than the Aligned Pair Exclusion described below but the funny thing is that XYZ-Wing is a total sub-set of APE. Every XYZ-Wing can be solved by APE (but not vis versa).

(Note: Turn OFF Unique Rectangles)
 XYZ-Wing eg 2
XYZ-Wing eg 2: Load Example or : From the Start
XYZ-Wing, Example 3 (same puzzle, a few steps further on): XYZ-Wing eg 3
XYZ-Wing eg 3

breakline

Comments...

Saturday 8-May-2010

... by: Nassir M

Why not to also remove the 5 on F4 as long as the 5 going to be either on B4 or E4 ?
Nassir.


Thursday 8-Apr-2010

... by: VISWA G

Reference XYZ-Wing eg 2, the logic behind the elimination of 7 from
R4C9 is understood and appreciated.
Elucidate the logic how 6 is confirmed out of 6/7 at R3C5 at XYZ-Wing eg3 by eliminating 7 from R4C9.
I tried to solve the same puzzle to the best of my ability but I failed to solve this. I will be grateful if I get help.


Add your comments

A confirmation email will be sent to you after submitting.

Your Name

Email Address - required for confirmation (it will not be displayed here)

Your comment or question

Remember me


Please keep your comments relevant to this article. Email addresses are never displayed, but they are required to confirm your comments.

When you enter your name and email address, you'll be sent a link to confirm your comment. If you want to be remembered, the check box above will store a cookie with your name and email address on your computer.

Line breaks and paragraphs are automatically converted — no need to use <p> or <br> tags.



Article created on 11-April-2008. Views: 19648
This page was last modified on 11-April-2008, at 20:20.
All text is copyright and for personal use only but may be reproduced with the permission of the author.
Copyright Andrew Stuart @ Scanraid Ltd, 2008