Sue-De-Coq
This exotic strategy is strongly related to trivial patterns like Naked Pairs and Naked Triples since we are identifying Locked Sets. The building blocks are Almost Locked Sets but the most interesting aspect is the alignment of these parts.
To re-cap the terms:
To re-cap the terms:
- A Locked Set is a group of N cells that can see each other which have N candidates - an example being a Naked Pair
- An Almost Locked Set is a group of N cells which are mutually visible and share N+1 candidates in some combination.
- An Almost Almost Locked Set is a group of N cells which are mutually visible and share N+2 candidates in some combination.
- An Almost Almost Almost Locked Set is a group of N cells which are mutually visible and share N+3 candidates in some combination.
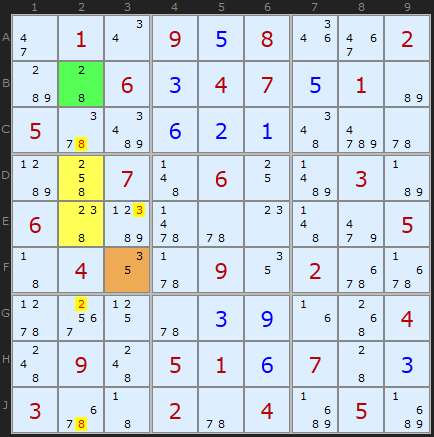
In the first example the two yellow cells (N=2) contain {2,3,5,8} which is N+2, or four candidates. The group is contained within box 4. We don't know which of the values {2,3,5,8} will be the solution to D2 and E2 but clearly two of those four will be. Now, if we look along the unit of alignment (column 2) and within the box we can find single cells that contain two of those candidates. B2 contains {2,8} (the green cell) and F3 contains {3,5}. The AALS can see these cells - which is important!
We now know that the solution to the AALS {D2,E2} cannot be 2/8 or 3/5 since it would leave nothing in the cells B2 and F3.
The logic is as follows. If neither {2/8} can fill the AALS nor {3,5} then some other combination must fill it that leaves a digit free for the single bi-value cells. So effectively {2,3,5,8} must fill all coloured cells. Indeed the group in total contains four cells and there are four candidates, so we have identified the total group as a Locked Set. This means we can remove all candidates X that see all X in the total group. This excludes the 8 in C2 and J2 (aligned in the column) and 2 G2 (also aligned in the columns) and the 3 in E3 (shares the box).
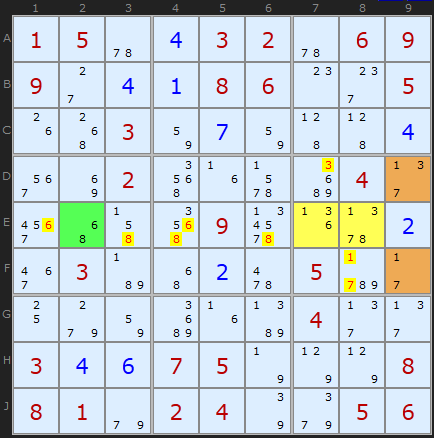
In the second example we combine an AAALS (N+3) in {E7,E8} containing {1,3,6,7,8} with two normal ALSs {D9,F9} and {E2} containing {1,3,7} and {6/8} respectively. The trick is that the total number of cells, 5, equals the total number of candidates in all the cells {1,3,6,7,8}. We get a 5-cell Locked Set.
To eliminate we look at what candidates OUTSIDE the pattern can see ALL the candidates INSIDE the pattern. These are the 6s and 8s in row E, and the 1s, 3s and 7s in box 6.
Generally then...
The general terms the rule for the pattern is as follows:
- Find a 2-cell or 3-cell group inside a box that is also aligned on a row or column - call it group C
- C contains a set of candidates, V, which must be two or more than the number of cells in C (N+2, N+3 ALS etc).
- We need to find at least one bi-value cell (or larger ALS) in the row or column which only contains candidates from set V, called D
- We need to find at least one bi-value cell (or larger ALS) in the box which only contains candidates from set V, called E
- The candidates in D and E must be different.
- Remove any candidates common to C+D not in the cells covered by C or D in the row or column
- Remove any candidates common to C+E not in the cells covered by C or E in the box

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Cerberus
The Sue de Coq was originally called 'Two Sector Disjoint Subset', where sector means a house and disjoint means they are separated from each other. Sue de Coq is often abbreviated to SDC.
The structure of the SDC
---------------------------------
The SDC consists of 3 separate groups of unsolved cells. For each SDC, there needs to be a group of 2 or 3 cells that exist in the same row or column within the same 3x3 block. These cells, that I have labelled C, must contain at least two more candidates than there are cells, the candidates existing in C have been labelled, Cc. In the same 3x3 block that C resides in, there must reside another group of cells, which I have labelled B, the candidates of B have been labelled Bc. It is possible for B to be just a single cell. There must always be at least two candidates in Bc that are members of Cc. A third group of cells must exist in the same row or column, that C resides in, similarly to B, this group of cells can also be just a single cell. This third group of cells I have labelled A. The candidates of A have been labelled Ac and similar to Bc, must contain a least 2 members of Cc.
Constraints/Criteria
--------------------------
All cells of C must be in the same 3x3 block and must be in the same row or same column.
There must be at least 2 more candidates in Cc than there are cells of C.
All cells of A must be in the same row or column that C exists in.
All cells of B must be in the same 3x3 block that C exists in.
No cell of A, B or C can be shared.
There must never be a candidate that is common to Ac, Bc and Cc.
At least two candidates of Ac must exist in Cc.
At least two candidates of Bc must exist in Cc.
The number of cells in the whole SDC construct (i.e. cells A, B and C) must equal the number of different candidate values in the collective subset of Ac, Bc and Cc, plus (if any), the number of candidate values that are common to Ac and Bc.
Potential Eliminations
----------------------------
Any unsolved cell, not in A, B and C, that can see every cell of A and C, which contains a candidate from Ac, then, that candidate can be removed.
Any unsolved cell, not in A, B and C, that can see every cell of B and C, which contains a candidate from Bc, then, that candidate can be removed.
Comments
--------------
Whilst the labels, A, B and C may refer to different groups elsewhere, I decided to arranged to serve as a mnemonic device. C was used to represent the 'core/center' of the SDC, whilst B was used to represent the set of cells residing in the same 3x3 'block' as the core, finally, A was used because its cells 'aligned' with those of the core.
... by: Megastar
https://sudoku.megastar.fr/larme-et-la-soie-sue-de-coq/
... by: Cerberus
... you say, generally, the candidates in D & E must be different.
... is that, collectively different, or singular different, would 2, 3 in one, be okay, if 3, 6. was in the other, or must all instances of a 2 or a 3 be absent?
... by: Jonathan Handojo
So my simplest way of understanding this is: Where you have a Locked Set and all of its candidates in it are restricted commons (i.e. where all instances of each and every one of those candidates that can see each other), you can eliminate any other candidates outside that locked set that can see every instance of those candidates within that locked set.
This is why there's a lot more elimination in the Sue-De-Coq rather than the WXYZ Wing.
Wxyz wing is an als xz move with up to 2 rcc,
Which precisely mimics suede coqs that only occupies 4 cells,
The diffrence is that a sue de coq can be any n size als with n +x degrees of freedom(where x=9-n at max),
we have examples in the forums for als dof = 7 sue de coq
That has no equivalent als xz move debunking the od adage that all sue de coqs where only als xz with 2rcc
Strmckr.
... by: Jan Laloux
It is not the ordinary locked set, but what I call a "dispersed locked set". In a normal LS all cell involved are bound to one unit. In a DLS there is no such restriction. I have not seen this described anywhere else so far.
You have a DLS of size n when you have n cells anywhere in the grid with in total n digits, with the requirements that for each digit all candidates for that digit are bound to one unit, and that all cells are "connected". The latter condition is a bit more complicated to explain. I'll demonstrate it with a colouring procedure: colour the first cell, then for each digit that is a candidate in that cell colour all other cells in the set that have that digit as candidate, repeat the procedure for all the newly coloured cells. At the end all cells in the unit must be coloured.
In the first example above we have a DLS of size 4 with cells B2, D2, E2 and F3 and 4 digits 2, 3, 5 and 8. Digits 2 and 8 are bound to column 2, digits 3 and 5 to box 4. The eliminations follow the same logic as with an ordinary LS, resulting in the eliminations shown in the SdC example.
There are in the same way also hidden DLS, dispersed almost locked set (DALS) etc. My solver uses DALS wherever an ALS can be used such in an AIC, death blossom, unique rectangle type 3 etc.
... by: Teige
... by: Sherman
The first extension is that C can contain candidates not in D and E. This is a possibility if C is N+3 or larger. If C has one or more candidates not in D and E, these candidates can be removed in the cells not covered by C+D+E in C's box and row or column.
The second extension is that D and E can contain candidates not in C, as long as D and E each contain at least one candidate from C. The candidates in D and E must still be different. The rule saying D and E must be a subset of C is not needed. The two removal rules are modified to say that the candidates from D can be removed from the cells not covered by C+D in C's row or column and the candidates from E can be removed from the cells not covered by C+E in C's box.
This works because C+D+E is a locked set and D and E are mutually exclusive. Between C+D+E, all possible locations of their candidates are fixed.
This is not my work. I found it by perusing other Sudoku websites.
... by: SudoNova
I think the highlighted cells with digits13678 in example 2 are exactly this.
Following my strategy described in WXYZ-wing, the green-highlighted cell
contains the digits WZ (or perhaps VZ here) and the red highlighted digits
68 in row E are the rogue Z's
... by: Prasolov V.
... by: Herbert Jensen