Intersection Removal
If any one number occurs twice or three times in just one unit (any row, column or box) then we can remove that number from the intersection of another unit. There are three types of intersection:
- A Pair or Triple in a box - if they are aligned on a row, n can be removed from the rest of the row.
- A Pair or Triple in a box - if they are aligned on a column, n can be removed from the rest of the column.
- A Pair or Triple in a box - if they are all in the same box, n can be removed from the rest of the box.
Pointing Pairs, Pointing Triples
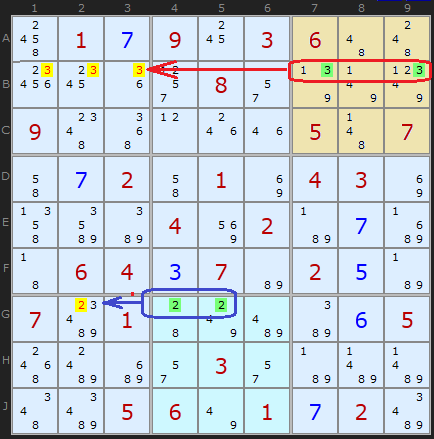
Here are two Pointing Pairs at the same time on this tough rated puzzle. The 3s in B7 and B9 are alone in box 3 and they are aligned on the row. So looking along the row we can remove all the 3s in Box 1. In a similar manner the 2s in G4 and G5 point along the row to G2.
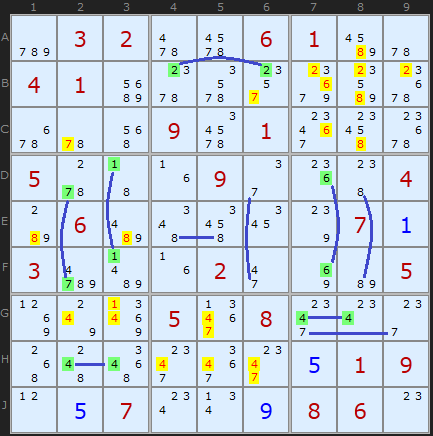
Now this is a rather special puzzle and a little extreme, but if we look at the whole board you can see I have highlighted a whole cluster of Pointing Pairs. It is obviously not necessary to spot everyone to progress the board but there are so many good examples it is worth looking at. The eliminations are highlighted in yellow. You should be able to see which eliminations belong to which Pointing Pair. A couple are consequences of a previous elimination.
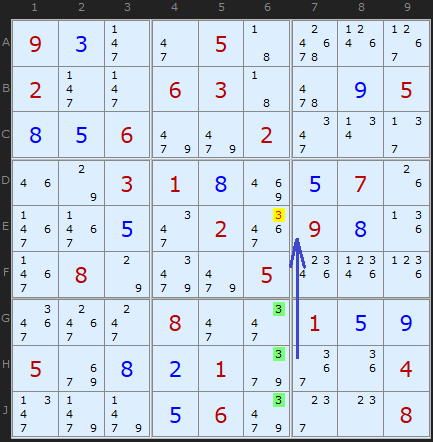
Here is a Pointing Triple found in a tough grade puzzle containing many wholesome and nutritious Pointing Pairs. All the 3s are found in G6, H6 and J6 and nowhere else in box 8, so they point up the column to another 3 which can be removed.
Box Line Reduction
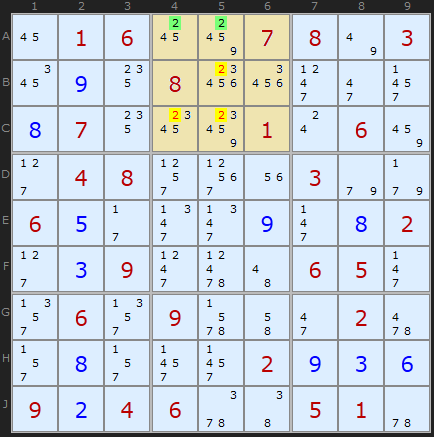
This Sudoku contains numerous Pointing Pairs and Box/Line Reductions and is worth stepping through from the start. Consider row A. The only 2s left are in A4 and A5 which means we should check the rest of the box. 2 has to go somewhere on row A and it will be in one of those two cells. So we can eliminate 2 from B5, C4 and C5.
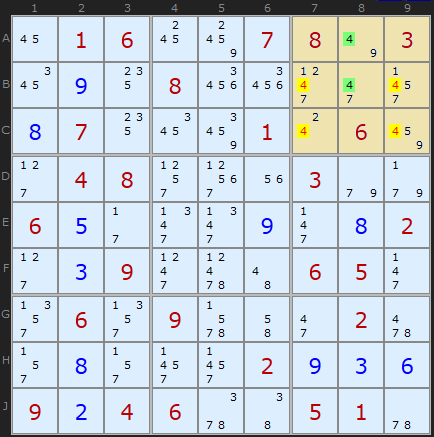
In the very next step of the same puzzle we have two 4s alone in column 8. That fixes 4 to be in either cell A8 or B8. We can remove the other 4s in box 3 and get our next solved cell: 2 in C7.
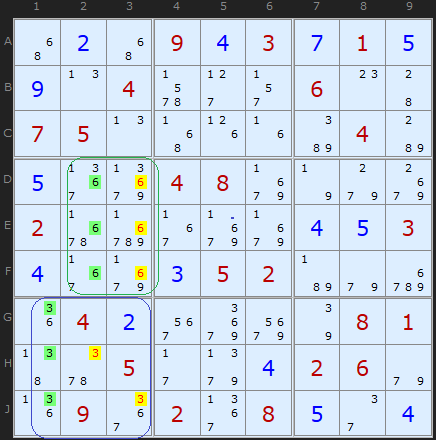
I've rolled two examples into one diagram here, I hope it wont be confusing. The one involving 6s follows on immediately from the first one found among the 3s (purely because it searches in order from 1 to 9). They are both 'triple' versions of Box/Line reduction.
In column 1 the 3s occupy G1, H1, J1 (shorthand = GHJ1) which are all in box 7. The solution is pinned to column 1 so the other 3s in the box must go.
The 6s are likewise pinned by column 2. You can see there are other 6s in column 3, in A3 and J3) which is why it's okay to remove the 6s in DEF3. You won't run out.
If you are a fan of Jigsaw Sudoku puzzles, you may want to read the articles on Double Pointing Pairs and Double Line/Box Reduction which extend the ideas here but are strategies possible only in the Jigsaw variant of the puzzle.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Udimu
Points 3. & 4. can be merged into
3. A Pair or Triple in the same box, n can be removed from the rest of the box. They do NOT have to be aligned in a row or column.
... by: Aws
... by: Sebastian G.
Personally, I detect the "Multiple Lines" Pattern more easily and quickly (given that the candidates of a number can be highlighted) than I do the "Box/Line Reduction". I think it might be worth describing this pattern here.
... by: joe
I tried to read about intersection removal on other websites, but only after reading this article and using hints on Sudoku Mood a couple of times I finally understood how to use this method.
... by: d4m4s74
So far I've built everything up to pointing pairs,and my project for tomorrow is Box Line Reduction.
Shall I just go on in order, or do you recommend specific steps to do next to be able to solve most puzzles?
(If you want to check it out you can find my code so far on github, using the same name as I'm using right now)
... by: Robert Jones
Incidentally, I had trouble sending this comment because I followed the instruction 'to the letter' and didn't enter the number. It should say " Please enter the characters you see"!
... by: Oldray26
... by: Edwin McCravy
... by: edgar cook
thanks
-eac
Best of luck with the project
... by: Emy
... by: James
... by: Paul
... by: Zaiyah
... by: AlexB
I don't think this is the basis of the logic. What is important is that the digit does not occur in another unit. Maybe I should explain using the example given. In the first example, digit 3 can be removed from B1,B2 and B3. It is stated that this is because there is a pair of 3's in B7,B9. However, what is important here is that there is no 3 on A7,A8,A9,C7,C8,C9. The amount of 3's in B7,B8,B9 makes no difference, the same logic works for 1, 2 or 3 of them.
In other words: I believe explaining this technique using pairs and triples masks the real logic used.
Am I missing something?
... by: YBB
... by: Robert
I just wanted to thank you for the excellent site.
You explanations and examples are brilliant!
You obviously put in a tremendous amount of time and effort creating this site. You are to be congratulated!
Thanks
Robert
... by: Ken
How has number 2 been eliminated as a candidate for cells A1 and B1?
There is no number 2 present in that box, or in row A or column 1
I assume the number 2 has already been eliminated from these cells at a previous stage, using the pointing pair of 2s in row A. However this is not made clear when the example is viewed in isolation.
... by: VG100
Thank you so much for clarifying both these strategies.
Playing the game is going to be so much more fun and I can comtinue to challenge myself!
Many thanks.
... by: jb681131
... by: Mal
... by: Y.Sato
... by: TomSellek
Now, from this fact, we can conclude: in row B, there may be no other '3' set. If there were some hints of Digit 3 elsewhere in row B (let alone box 3, this box remains untouched and we could not decide now, which of B7 or B9 would really be true, finally), all those hints in row B could now be removed (look at B1...6), so in this example: B123.
Now your question about "why do the 3s in box 1 do not mean anything". It's going like this: neither, the 3's in box 1 are restricted to row B (there are 3's in C2, C3), nor, the 3's in row B are restricted to box 1 (because of the 3's in box 3). Conclusion: you CANNOT conclude any reduction of pencilmarks out of the 3's in box1.
I hope I could help you, gretchen
... by: Gretchen
... by: JG
I am delighted to have found your excellent site. I am still at the intermediate level but have found your explanations totally understandable, not something I can say about some others!
Thank you.
... by: Joseph Boronka
I been playing Soduko for 3 yrs now, and still trying to figure out ways to solve them,
your web-site helps a lot with tips and hints.
here is a cool puzzle, and it looks good too !
it has 1 unique solution and is solvable.
... by: George kunnappally
... by: ajay
your puzzle solving methods very charming, I do like it .hence forward I will fallow
your tricks to solve the puzzle. Thank-u very much. I do fallow till I get to hard puzzle.
bye-bye
AJAy
... by: Ilma
... by: LizH
... by: Ed
... by: Konrad M Kritzinger
... by: Anthony
58 1589 1589
2 6 14789
78 4789 3
... by: Paleo3D
... by: alvin
... by: CS VIDYASAGAR
Thanks for nice and simple elucidation of difficult concept.
... by: Patrick Barnaby
There is an X-Wing for sevens and an X-Wing for eights.
... by: Clell
I had looked at this and also could not see the relationship until I reread the above and saw there were no other alternatives in the pointing pair box that forced the others to be eliminated. thanks
... by: Greg
... by: grosenthal08
... by: Rick Aben
The same counts for "type 2" (with a swap of box and rows). In that example the two 9's can be found in the intersection of row 4 en box 6 (the box on the right) and not in the remainder of row 4, which means the 9's in the remainder of box 6 can be eliminated. Ofcource, the solution is the same, the difference is in the logical explanation. Isn't it?
... by: Sergio Scarabello
What prevents the choice of pointing triples of 2 in B7-B8-B9 or even the choice of pointing pairs of sny combination in that box, which would lead to elimination of B4-B6?