Strategies for Number Puzzles of all kinds
 
 
Print Version
 
Solvers
Puzzles
Basic Strategies
Tough Strategies
Diabolical Strategies
Extreme Strategies
Depreciated Strategies
Str8ts
Other
The Logic of Sudoku
Order Str8ts Book 1
Order Now!
Order Str8ts Book 2
Order Now!
  Weak and Strong Links
This article continues from Introducing Chains and Links. Recommended reading if you have not done so first.

Here I clarify certain terms scattered about the strategies and put them in one place for easy reference and well as grow the theory on how chains are formed. These terms include Weak and Strong Links, or more accurately, links with weak or strong "inference". They were introduced in the X Cycles strategy but have wide application.


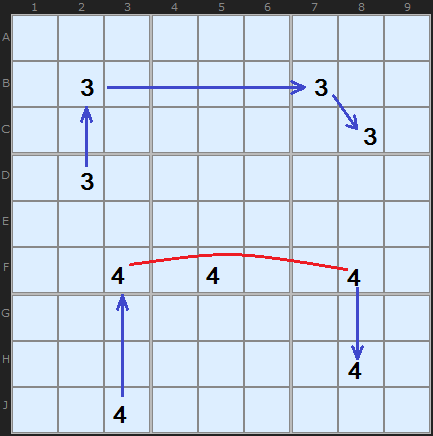
In this diagram I am showing two short chains. Infact, only the top one using 3's is a chain since all the component candidates are conjugate pairs. The problem with the bottom chain is that there are three 4s in row F. The red line indicates the potential link that fails because the 4s on the row are not bi-location 4s.
Figure 1
Figure 1
But, there is another way of thinking about chains and it directly relates to the ON/OFF states that all the candidates must have.

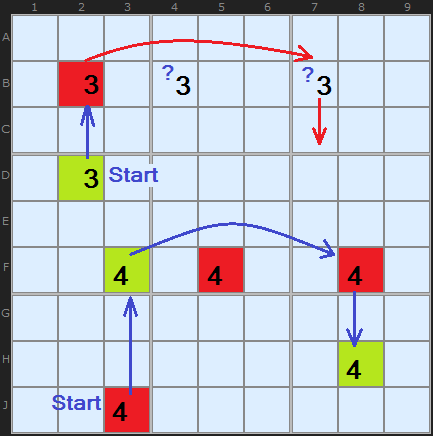
In the diagram I show the same chain of 4s but offset into different parts of the board. The start cell is essentally the same. In the uppser chain the start cell D2 is ON which causes the 4 in B2 to go off. Now, since there are two remaining 4s in row B the consequence of the OFF state in B2 ends. We don't know which of B4 or B7 to turn on.

But if we change the start state to OFF, as in J3 this causes F4 to be ON. When a candidate is turned on it turns off ALL the other candidates in all units it can see. Including the 4 in F8. So there is a conseqence and the chain can continue to H8. 		Figure 2: Two Chains on 4
Figure 2: Two Chains on 4

A fuller example: Figure 3 marks out a classic X-Wing. X-Wings always contain four numbers arranged in a rectangle such that two opposite sides contain just two remaining candidates of a certain number, in this case 9. Such pairs are minimal 1-link chains, or simply bi-location pairs. If our X-Wing was a 4-link loop containing just conjugate pairs then it wouldn't be interesting - there would be no eliminations.

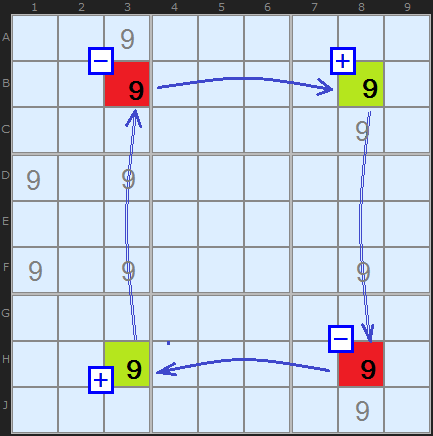
In Figure 3 the two pairs are at {B3,B8} and {H3,H8}. From a pair it is possible to draw two separate inferences, called weak and strong:
  1. If one cell is the solution then the other cannot be - link of weak inference
  2. If one cell is NOT the solution the other must be - link of strong inference
 Figure 3: Nice Loop on 9
Figure 3: Nice Loop on 9
In other words, a strong link is where:

!A => B (if not A, then B) OFF implies ON

Weak links are the opposite:

A => !B (if A, then not B) ON implies OFF

Back to the diagram. Consider the columns 3 and 8 which are part of the X-Wing and are marked with thin double lines. Because there are more than two 9s in the columns we can't draw a strong inference. We can only draw a weak inference, that is, if one of those 9s is the solution all the other 9s are eliminated.

Strong can be Weak

So far the rough and ready distinction between Strong and Weak links is to do with how many candidates are in a unit – namely, Strong links are formed when only two are present, while three or more imply a Weak link. However, this is not the case.

From a strong link we can infer that
if not A, then B

From a weak link, we can infer only that
if A then not B, C, D according to how many candidates there are in a unit

However, the following is also true that for a strong link:
if A, then not B

So, some Strong links can be reversed to give us a "link with weak inference" - if the occasion calls for it. It is perfectly logical to assert on a unit with two candidates of X both:

  • If Not A then B (!A =>B)
  • If A then Not B (A => !B)

In Figure 4 we have an array of 6 candidates on a board. A number of strategies can show that the 6 on H9 can be eliminated. I have coloured some cells using Singles Chains Rule 5 which link up some pairs on the board - either all of the yellow cells will be 6 or all of the cyan cells will be 6. Since H9 can see C9 (yellow) and H5 (cyan) it cannot be a 6 since it can see cells with both colours.

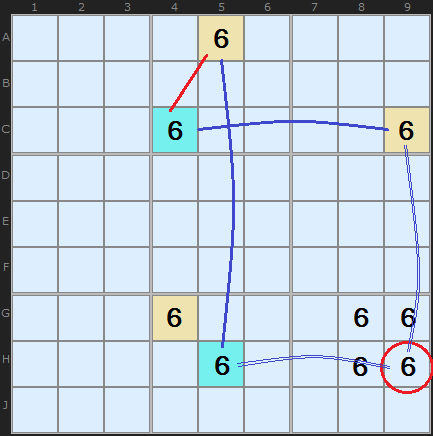
To take the Nice Loop example from X-Cycles, we can draw links I have done with blue lines. Our aim is to show that the circled 6 on H9 is eliminated because there are two weak links forming a discontinuity. That is all correct and invokes Nice Rule 3. But take a look at the red link {C4,A5}. It is a Strong Link with Weak Inferemce. It is a Strong Link because there are only two 6s in the box but it we are using it to imply that if A5 is a 6 then C4 is not and if C4 is a 6 then A5 is not. 		Figure 4: Strong Link with Weak Inference
Figure 4: Strong Link with Weak Inference
Constructing Exotic Links

This, amazingly, is not the end links in chains. Apart from bi-value and bi-location links there are other more exotic ways to form a link in a chain.

You should read the article on Grouped X-Cycles to see how a group of candidates in several cells can be used to form a link.

Also, Almost Locked Sets can be made into links. This method needs to be documented but it is present in the solver.



 
Comments

Monday 14-Jun-2010

... by: Crizz

I am not satisfied with the logical explanations of strong and weak links, so try mine.
If A and B are the same candidates in different cells of one house then
a strong link is where:
A=>!B or !A=>B
a weak link is where:
A=>!B or (!A=>B or !B)
That means we cannot define the state of the candidate B in a weak link where the candidate A is false.
Please correct me if i'm wrong.



 Post a Comment using Facebook...
or post a Comment or Question here...
A confirmation email will be sent to you after submitting.

Your Name

Email Address - required for confirmation (it will not be displayed here)

Your comment or question

Please enter the
letters you see:
 arrow		Enter these letters
Remember me


Please keep your comments relevant to this article.
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted — no need to use <p> or <br> tags.


Article created on 6-December-2008. Views: 12793
This page was last modified on 30-December-2011, at 14:14.
All text is copyright and for personal use only but may be reproduced with the permission of the author.
Copyright Andrew Stuart @ Syndicated Puzzles Inc, 2011