Empty Rectangles

Empty Rectangles constitute a clever but obscure strategy for Sudoku. An Empty Rectangle occurs within a box where four cells form a rectangle which does NOT contain a certain candidate.

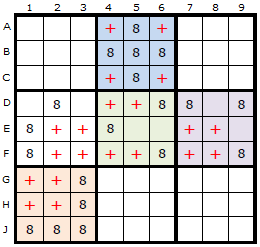
In the first diagram is a spread of candidate 8 around the board but each box must be considered separately when imagining the rectangle, so I have coloured the boxes differently. To be able to apply this strategy we must have at least two candidates left in the box and four or more empty cells.

The red crosses represent the Empty Rectangles. Each of these theoretical rectangles is independent of the others.

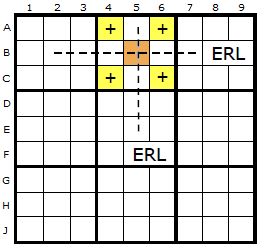
Whatever the formation of the Empty Rectangle (ER), we will have a vertical and horizontal gap where we can imagine two Empty Rectangle Lines (ERLs). These are two lines we can draw inside the box without touching the ER itself.

I have picked box two in this example.

We can quickly forget about these lines once we've spotted where they cross - a place known as the Empty Rectangle Intersection (ERI).

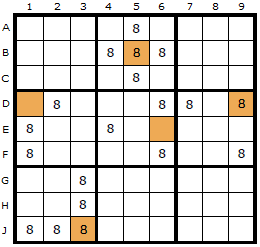
In this diagram the ERIs have been marked with a brown cell.

If you have a strong link and an ERI that shares a line (row or column), then you can eliminate a candidate at that point where the other end of the strong link and the ERI intersect. Let's look at some visual examples of the formation. Two different arrangements are shown in this and the next diagram.

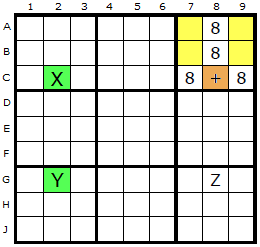
The plus sign now indicates where the Empty Rectangle Intersection (ERI) is placed. In the first example down column 2, two 8s exist and form a strong link (X and Y). One end of the strong link (X at C2) can see the ERI at C8.

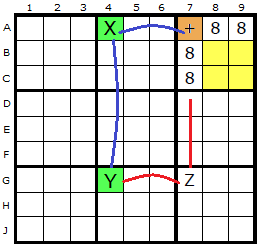
In the second example the ERI at A7 can see an 8 in A4 (the X) and this is paired with the 8 on the cell marked Y. Y can see the 8 in Z which in turn is visible to the original ERI.

It is proposed in both examples that the 8 in Z can be removed.

Here is a real example based on the centre box. The remaining options for 6 in box 5 is D4, D5, E6 and F6. This gives us an Empty Rectangle shown by the four yellow cells. The Empty Rectangle Intersection is the orange cell on D6. Our X and Y are the two green cells H6 and H9. It doesn't matter that there are a ton of 6s in column 6, what is important is there are two 6s in row H. H6 can see the ERI and H9 can see the intersection of H9 and the ERI - which is D9. That is the 6 we can remove.

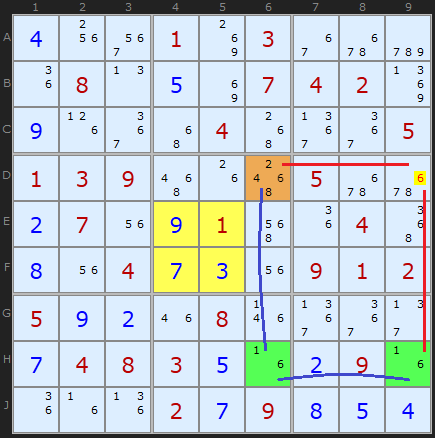
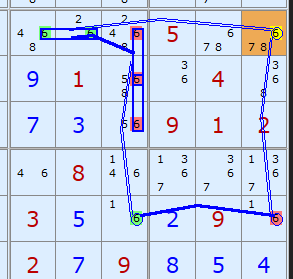
Here is the equivalent Grouped X-Cycle based on candidate 6.

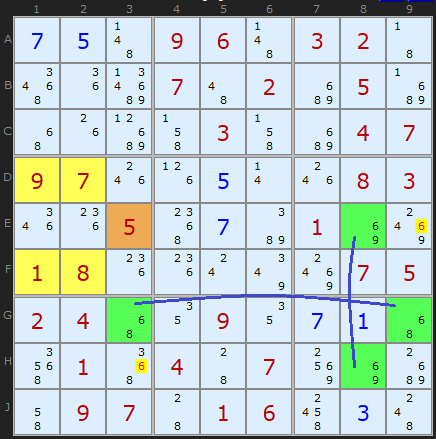
Here is a fascinating double Empty Rectangle. The ERI cell on E3 can see two strong links on candidate 6. There is one in row G between G3 and G9 and in the other in column 8 between E8 and H8. The first one allows us to remove 6 from E9 and the second from H3. Double the fun!

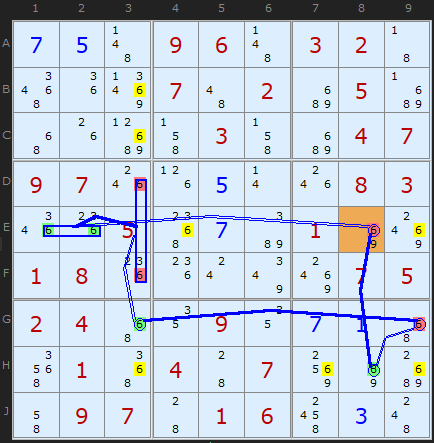
The equivalent Grouped X-Cycle based on candidate 6 gets many more eliminations since it's an off-chain continuous Nice Loop.

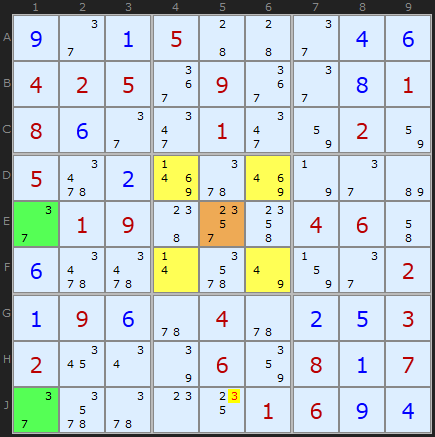
This awesome sudoku has great examples of certain strategies including a symetrical Hidden Quad. At this stage there is a perfectly centered Empty Rectangle based on candidate 3 with no clues in the rectangle cells. I have Klaus Brenner to thank for sending me this puzzle.

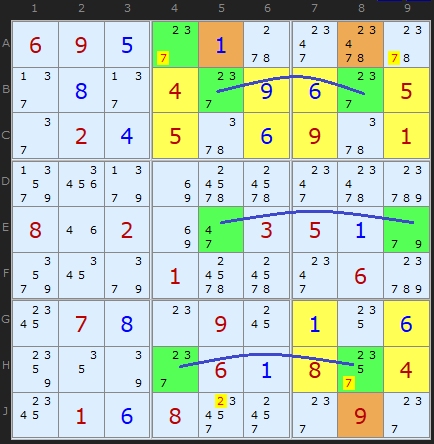
Klaus Brenner has found some very nice looking triple Empty Rectangles. I didn't think we'd find any beyond the double one above, but no, here is one of five he has made.

The solver normally returns just the first instance of an advanced strategy but in the case of Empty Rectangles it will return all instances. Klaus also found a puzzle that returns three different Empty Rectangles in a single step. You can load the puzzle from this link.