Grouped X-Cycles

Chaining strategies such as X-Cycles use links that connect cells on the board. It is possible to expand on the idea of a "cell" to something a bit larger, namely a "group" of cells. I prefer the word "node" - which in 90% of cases will be a single cell - but can be two or three cells in the same unit. You might wonder how we can use more than one cell and think of it as a node between two links, but there is some cool logic here.

We must go all the way back to Pointing Pairs and Pointing Triples. They attack cells along the row or column on which they are aligned. They also must be in the same box to be a coherent unit. Our “grouped” cells are just Pointing Pairs/Triples and we’re going to use them as part of a chain or Nice Loop.

Clearing the clutter on an example board, in Figure 1, we have a spread of candidate 4s. All the lettered cells are also candidate 4. There is a continuous Nice Loop starting with A. B-C is a weak link, and so is D-E.

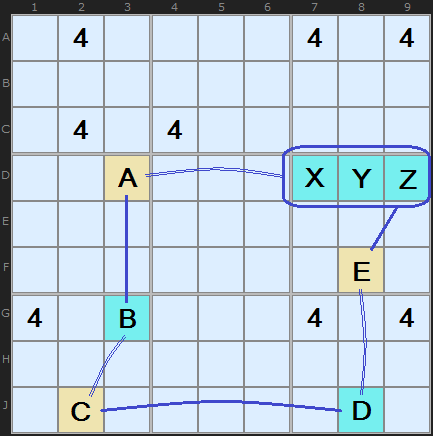
The interesting part is the set of cells [X|Y|Z]. It does not matter which of X, Y, or Z (if any) is the solution; any of them will eliminate A and E. Likewise, if E is true, then all of XYZ are gone – and A is true. We can think of [X|Y|Z] as a single node for the purposes of our logic. This promotes the links from A and E to strong links, and the notation for this part of a loop is:

+4[F8]-4[D7|D8|D9]+4[D3]-
 E     X or Y or Z     A

The important characteristic is that the cells are all in the same box. One end of the chain (in this case, A) is pointed to by the node cells; the other (in this case, E) is usually within the same box as the node.

At the point it's also worth re-capping something about Continuous Alternating Inference Chains. Firstly, its doesn't matter which way you walk round the loop - clockwise or anti-clockwise, secondly, it doesn't matter which cell you start with and thirdly, each cell could be ON or OFF - as long as you alternate. Even with the convention of starting with the top left-most cell, there are four ways we could write down the chain:

• Clockwise with D3 ON   +4[D3]-4[D7|D8|D9]+4[F8]-4[J8]+4[J2]-4[G3]
• Clockwise with D3 OFF   -4[D3]+4[D7|D8|D9]-4[F8]+4[J8]-4[J2]+4[G3]
• Anti-clockwise with D3 ON   +4[D3]-4[G3]+4[J2]-4[J8]+4[F8]-4[D7|D8|D9]
• Anti-clockwise with D3 OFF   -4[D3]+4[G3]-4[J2]+4[J8]-4[F8]+4[D7|D8|D9]

I've deliberately used neutral colours in the diagram above (yellow and blue) not to given the impression there only one way to write the same chain. However, the solver will return very positive red and green highlighting but that's because it has discovered one of those four ways first and discarded the other three identical ways.

Check the article on X-Cycles for a review of Nice Loop Rule 1 in a cycle that does not contain Grouped Nodes.

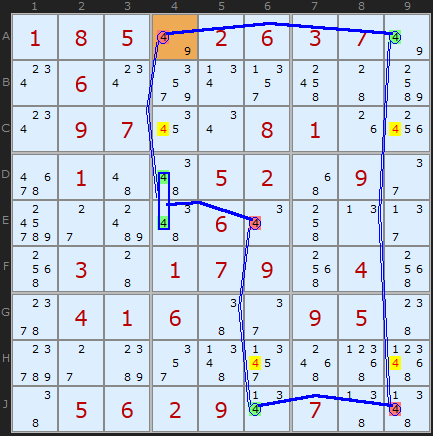
Figure 2 invokes Nice Loop Rule 1 - Off-Chain Eliminations. The output from the solver says:

X-CYCLE (Grouped Alternating Inference Chain) Rule 1:
-4[A4]+4[A9]-4[J9]+4[J6]
-4[E6]+4[D4|E4]-4[A4]
- Off-chain 4 taken off C9 - weak link: A9 to J9
- Off-chain 4 taken off H9 - weak link: A9 to J9
- Off-chain 4 taken off H6 - weak link: J6 to E6
- Off-chain 4 taken off C4 - weak link: D4 to A4

The Grouped node is [D4|E4] and it points up column 4 to A4 (a weak link since there is another 4 at C4. Three 4s can be eliminated in one fell swoop since all 4s that are on units with links of weak inference can go. These are highlighted in yellow.

This is a much more complex example, but it does show how powerful the strategy is in tackling a bottleneck on the board. The Nice Loop contains two Grouped nodes at [G7|G8|G9]-8[G2] and [G3|J3]. The first points along the row to G2. The second is aligned on column 3 and points to D3. All other 8s in any unit shared by any of the Weak links can be removed (Nice Loop Rule 1).

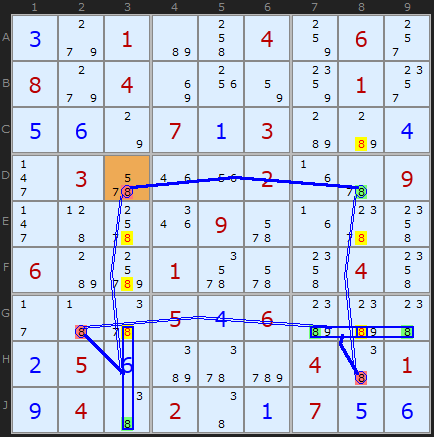
X-CYCLE (Grouped Alternating Inference Chain) Rule 1:
-8[D3]+8[D8]-8[H8]+8[G7|G8|G9]
-8[G2]+8[G3|J3]-8[D3]
- Off-chain 8 taken off C8 - weak link: D8 to H8
- Off-chain 8 taken off E8 - weak link: D8 to H8
- Off-chain 8 taken off G8 - weak link: D8 to H8
- Off-chain 8 taken off G3 - weak link: G7 to G2
- Off-chain 8 taken off E3 - weak link: G3 to D3
- Off-chain 8 taken off F3 - weak link: G3 to D3

Check the article on X-Cycles for a review of Nice Loop Rule 2 in a cycle that does not contain Grouped Nodes.

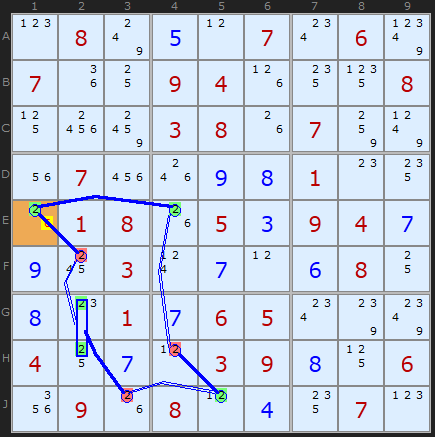
In Figure 4 we have a an X-Cycle on 2 (a 2-Cycle) with a group of two [G2|H2] usefully working together as a node. This allows us to create a chain linking the coloured cells on this diagram. From Rule 2 we can deduce that E1 must be a 2.

X-CYCLE on 2 (Grouped Discontinuous Alternating Nice Loop, length 8):
-2[E1]+2[E4]-2[H4]+2[J5]
-2[J3]+2[G2|H2]-2[F2]+2[E1]
- Contradiction: When 2 is removed from E1 the chain implies it must be 2 - other candidates 6 can be removed

In my second example in Figure 5 the chain is a little longer and eliminates two candidates when 8 is found to be the solution of cell G9. The grouped nodes is [D2|E2] and both 8s in those cells are being collectively turned OFF by the 8 in A2 pointing down to them. This link makes the chain possible.

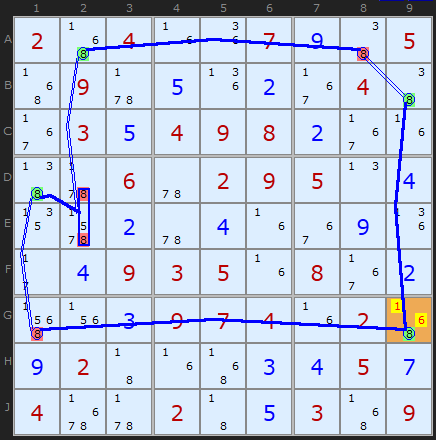
X-CYCLE on 8 (Grouped RC Discontinuous Alternating Nice Loop, length 8):
-8[G9]+8[B9]-8[A8]+8[A2]
-8[D2|E2]+8[D1]-8[G1]+8[G9]
- Contradiction: When 8 is removed from G9 the chain implies it must be 8 - other candidates 1/6 can be removed

Rule 2 examples are probably the least likely of the three rules to be found. Most grouped X-Cycles will be two weak links and Rule 3, next.

Rule 3 tells us that two weak links joined at H8 imply 2 can be removed from that cell. But the interesting part of the chain is the grouped cell in [A8|B8]. The chains comes along row 3 from C4 (ON) and forces 2 to be OFF in C9. That still leaves two more 2s in box 3, but they are nicely aligned on column 8. So we don't care which one may be the solution, only that they point down the column to H8.

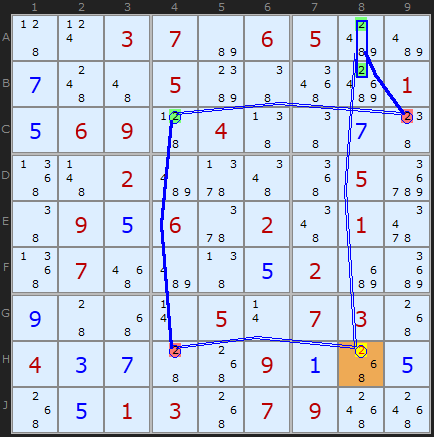
X-CYCLE on 2 (Grouped Discontinuous Alternating Nice Loop, length 6):
+2[H8]-2[H4]+2[C4]-2[C9]+2[A8|B8]-2[H8]
- Contradiction: When H8 is set to 2 the chain implies it cannot be 2 - it can be removed

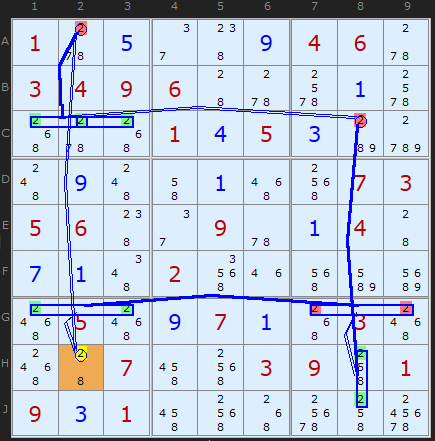
A particularly nice Grouped X-Cycle on 2 appears in this puzzle. Row G shows that we can occasionally expect to see two Grouped Cells in the same unit consecutively - provided the entry and exits are available. One will be positive (ON) and the other negative (OFF).
+2[H2]-2[A2]+2[C1|C2|C3] -2[C8]+2[H8|J8]-2[G7|G9] +2[G1|G3]-2[H2]
When H2 is set to 2 the chain implies it cannot be 2 - it can therefore be removed

Patrick Fischer sent me this puzzle

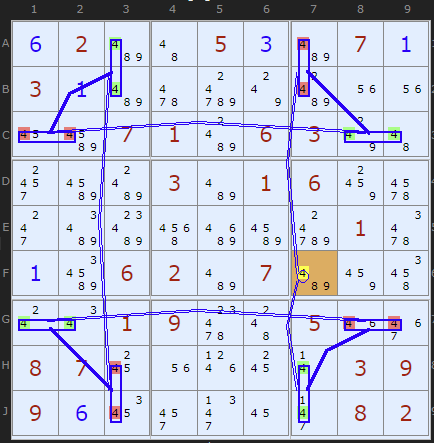
To finished off I must include this brilliant find by Klaus Brenner.
Eight Grouped Cells in a single X-Cycle on 4.

+4[F7]
-4[A7|B7]+4[C8|C9]
-4[C1|C2]+4[A3|B3]
-4[H3|J3]+4[G1|G2]
-4[G8|G9]+4[H7|J7]
-4[F7]
- Contradiction: When F7 is set to 4 the chain implies it cannot be 4 - it can be removed

Note: we can also see a contradiction at the start when F7 is set to +4: it not only causes -4[A7|B7] it also causes -4[H7|J7] so when the chain swings round to make +4[H7|J7] we have conflict and that also proves F7 cannot be 4.