Jellyfish Strategy

Jellyfish extends Swordfish one further row and column. We are looking for either

• four rows such that, in total, four cells are occupied in the row by a candidate number; or
  
• four columns such that, in total, four cells are occupied in the column by a candidate number
  

If this configuration is found then we can look in the opposite direction (if by row then down the column, if by column then across the row. If any candidates are found they can be eliminated. After the elimination both conditions above will hold.

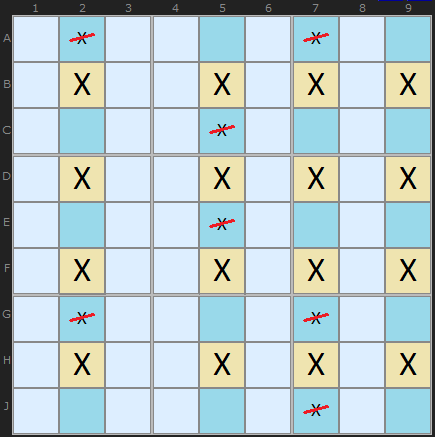
This diagram shows a full Jellyfish with four X found in four columns and aligned on four rows. It means we can remove any X found in the columns and it leaves behind a 4 by 4 grid.

How does it work? Pick any yellow cell in the example above that contains an X. Keeping an eye on it. Pretend the solution actually is X. All others Xs in the row and columns are suppressed. What we're left with is a Swordfish. The Swordfish logic then applies. Pick any X in the Swordfish and it reduces to an X-Wing. Since any combination of Xs on the grid are possible there is no room for Xs outside the grid - that align on the grid rows and columns.

Finding exactly candidate X in all sixteen cells (a 4-4-4-4 formation) is extremely unlikely. But the logic of Jellyfish (and Swordfish) is that we only need four X in total over the four rows and columns. Here is a minimal spread of a particular candidate X - a 2-2-2-2 formation. Most of the time you will have a mixture of two, three or four candidates lined up.

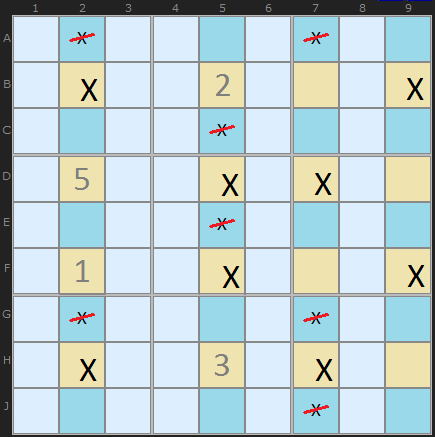
One way to double check the logic is to pretend any of the crossed out Xs is a solution. When you do that and trace the consequences you will find at least one row (or column) with no X left - clearly a bad consequence.

This is a real Jellyfish example, one of the very few I have that does actually show up in the solver - a crazy hard extreme. It is based on the candidate 7 as show by the green highlighted candidates. The cells in the pattern are orange. The pattern establishes that we have 7 common to four rows (B,D,E and H) which are aligned on four columns (1,5,7 and 9). Therefore four 7s must go in those yellow cells.

This is a 2-3-3-2 formation Jelly Fish since there are 7s absent in B1 and H2.

I am pleased to report a massive catch by Klaus Brenner from Germany. He has created a 31 clue Sudoku with a required JellyFish containing an amazing 18 eliminations.

Well done Klaus!

8th October 2012

(Turn off Rectangle Elimination)

To my knowledge this is the first Perfect 4-4-4-4 Jellyfish. Perfect in the sense that every 2 in the sixteen cells that form the pattern - the 2 is still a candidate. In the examples above, each contain some cells that are clues or solutions. This type of formation is pretty rare in Swordfishes, let alone Jellyfish. Klaus Brenner also found this puzzle.

13th July 2014

I have a new crop of Jelly-Fish discovered by Klaus. This one is a maximally eliminating pattern taking off all twenty 9s.

Jellyfish Exemplars

These puzzles require the Jellyfish strategy at early on (but are diabolical puzzles overall).
They make good practice puzzles.
All discovered by Klaus Brenner

• Exemplar 1 (score 915,perfect JF)
• Exemplar 2 (score 944,perfect JF)
• Exemplar 3 (score 665,perfect JF)
• Exemplar 4 (score 948, 19/20 eliminations)
• Exemplar 5 (score 1416, 19/20 eliminations)

Exotic variations of the Swordfish continue with the Finned Swordfish and Franken Swordfish.