Rule of 21 and Rule of 720 "large"

I have separated out from Rule of 21 and Rule of 720 an extension of those strategies which is clever but complicated to calculate. It is very much the last thing you should try on a stuck KenKen puzzle. But it does lead to a good number of break throughs and is logical. Many thanks to Roger Taft again for finding the examples and calculations.

To re-cap - we check every row, column and sets of adjacent rows and columns - called 'blocks'. in Rule of 21 we want to find all the cages in a block we know the SUM of which are all cages with the + clue and any where we can calculate the + value given the remaining candidates. With Rule of 720 we are interested in the PRODUCT of all the cages with x plus any cage where the x values can be calculated. When we know this value we can subtract/divide it from the block value (21 or 720 per row/column) and get the remainder. The unknown cages must SUM or MULTIPLY to this remaining value.

The solver 'standard' Rule of 21 and 720 puts the remaining unknown cells into 'pseudo-cage' but can only cope with a maximum of four cells. I have pre-calculated all the cage combinations to up 4 which is not as simple as Killer since duplicate values can exist in KenKen cages where the cage 'dog-legs'. A pseudo-cage is worse. It is the remaining cells in a 'block' Because these remaining cells can be all over the place they can 'dog-leg' much more than strictly adjacent cells in a normal cage defined by the puzzle maker.

However this extension covers all pseudo-cages of size 5 to 12 - hence the "large" in the strategy name. What makes this strategy possible is we not longer treat the entire remaining set of cells as one big pseudo-cage - just the standard cages that are unknown in the block. To make things even simpler the solver avoids blocks with dangling cages - cages that are half in half out.

Lets breakdown this example. From the solver we get a good deal of information:

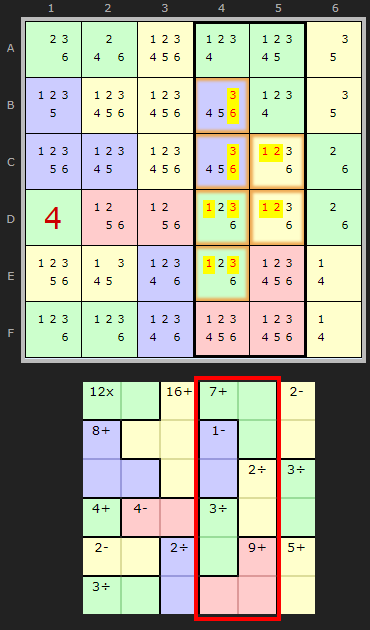
RULE OF '42', known cages:
A4 (7+) = 7
E5 (9+) = 9

In the two columns 4 and 5 we have two Known cages that sum to 16. Conveniently they are both + clues.

Remaining unknown cages must total 42-16 = 26

Given the remaining candidates must sum to 26 the following numbers fit the cells:

B4 C4 D4 E4 C5 D5 
 4  5  2  6  3  6 
 4  5  2  6  6  3 
 4  5  6  2  6  3 
 5  4  2  6  3  6 
 5  4  2  6  6  3 
 5  4  6  2  6  3 

so all other candidates must be removed

More examples to follow