| Main Page - Back |
|
From SudokuWiki.org, the puzzle solver's site |
Sudoku's Invariant Regions
The four red 2x2 cells in this diagram contain exactly the same set of numbers as the blue ring. This is true for every Sudoku.
I'm also endebted to Cracking the Cryptic for publishing this news with their commentary.
Phistomefle firstly sets out the case that the sum of the numbers in these cells is the same. To begin, all rows, columns and boxes total to 45 (the sum of 1 to 9).
Now there are two equivalent ways to sum the values in the red cells in this diagram
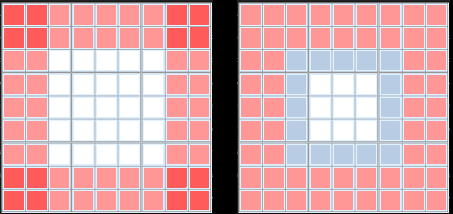
Secondly, instead of rows and columns we can also add up the eight boxes (45 * 8) and then subtract the values in the 16 blue cells in the ring. This also gives 360 - 80 = 280.
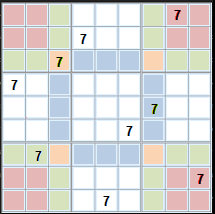
Taking rows C and G, columns 3 and 7 (and calling them lines), and the corner boxes we know that every number (7 for example) must appear must appear exactly once in each of the 4 lines and the 4 boxes. So if 7 appears in a
- green cell, this covers a line and a box,
- red cell, a box is covered,
- blue cell, a line is covered,
- orange cell covers two lines and one box.
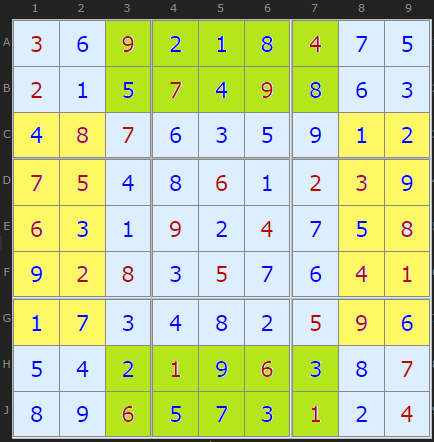
Yet this is not the end of the story. Taking the same puzzle as before we have complementary regions which are also invariant. There is the same set of digits in the green region as the yellow.
It turns out that the regions Phistomefle picked up on first are not unique.
Fred76 on the same thread, page 2 generalizes the idea with further dissections and even calculates that there are 15,876 combinations just for 4 rows and 4 columns dissections alone. He notes "This is why probably this technique is not practicable for human solvers - you can't check such big number of dissections."
He does draw an interesting parallel with the Fish patterns (X-Wings, Jelly Fish etc, and I can appreciate how the constraints do force regions to be complementary.
Interesting, but can it be used as a strategy in play, for very hard puzzles?