X-Wing Strategy

This strategy is looking at single numbers in rows and columns. It should be easier to spot in a game as we can concentrate on just one number at a time.

The picture on the right shows a classic X-Wing, this example being based on the number seven. The X is formed from the diagonal correspondence of cells marked A, B, C and D. What's special about them?

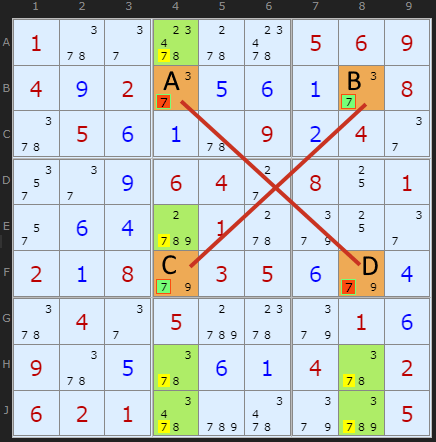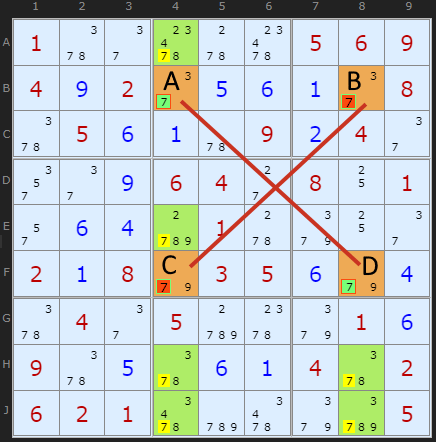
Well, A and B are a locked pair of 7s. So are C and D. They are locked because they are the only 7s in rows B and F. We know therefore that if A turns out to be a 7 then B cannot be a 7, and vice versa. Likewise if C turns out to be a 7 then D cannot be, and vice versa.

What is interesting is the 7s present elsewhere in the fourth and eighth columns. These have been highlighted with green boxes.

Think about the example this way. A, B, C and D form a rectangle. If A turns out to be a 7 then it rules out a 7 at C as well as B. Because A and CD are 'locked' then D must be a 7 if A is. Or vice versa. So a 7 MUST be present at AD or BC. If this is the case then any other 7s along the edge of our rectangle are redundant. We can remove the 7s marked in the green squares.

The rule is
When there are

• only two possible cells for a value in each of two different rows,
• and these candidates lie also in the same columns,
then all other candidates for this value in the columns can be eliminated.

The reverse is also true for 2 columns with 2 common rows. Since this strategy works in the other direction as well, we will look at an example next.

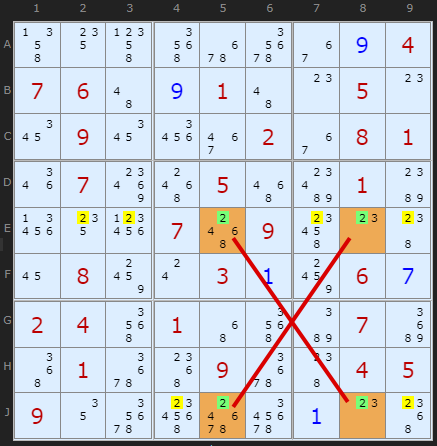
In this second example I've chosen a Sudoku puzzle where an enormous number of candidates can be removed using two X-Wings. The first is a '2-Wing'. The orange high lighted cells show the X-Wing formation. Note that the orientation is in the columns this time, as opposed to rows as above. Looking at columns we can see that candidate 2 only occurs twice - in the orange cells. Which ever way the 2s could be placed (E5/J8 or E8/J5) six other 2s in the rows can be removed - the yellow highlighted numbers.

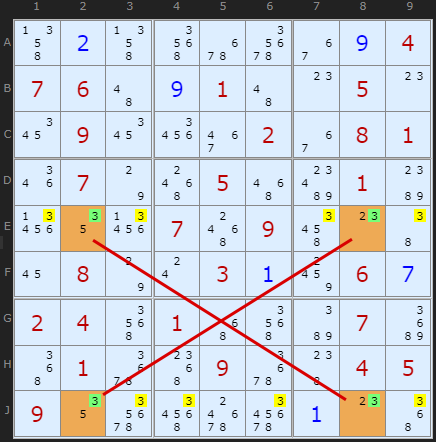
A few steps later the second X-Wing is found on candidate 3 in the same rows. Whichever way round the 3 can be placed in those rows (E2/J8 or E8/J2) there can be no other 3 in rows E and J except in those orange cells.

X-Wing is not restricted to rows and columns. We can also extend the idea to boxes as well.
If we generalise the rule above we get:

When there are

• only 2 candidates for a value, in each of 2 different units of the same kind,


• and these candidates lie also on 2 other units of the same kind,

then all other candidates for that value can be eliminated from the latter two units.

Now we have 6 combinations:

Here is an example of combination 5. Starting from 2 rows and eliminating in 2 boxes, in this case the last two boxes in the Sudoku. The rows are 7 and 8 and they each have two 7s. Our x-Wing is now a trapezoid but the logic is the same. We can be certain that 7 can be eliminated in the red circled cells.


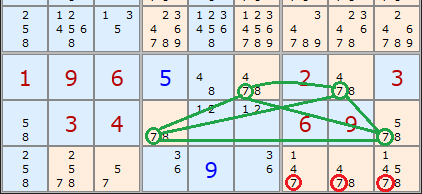
But HOLD UP one moment. There is a simpler strategy that does the same job!


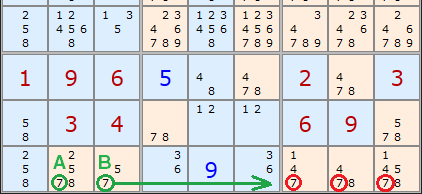
A and B above are a pointing pair. This removes the same 7s in the same place. Combination 6 is also the complement of a pointing pair. Combinations 3 and 4 are also complements of the Line/Box Reduction. Our generalisation of X-Wing to boxes hasn't profited us at all. We learn that

X-Wings containing boxes are the inverse of the Intersection Removal strategies

X-Wing Exemplars

These puzzles require the X-Wing strategy at some point but are otherwise trivial.
They make good practice puzzles.

• Exemplar 1, x1 (score 80)
• Exemplar 2, x1 (score 82)
• Exemplar 3, x2 (score 174, +1 Naked Pair)
• Exemplar 4, x2 (score 178, +1 Naked Pair)

The next strategy in this 'family' is Sword-Fish