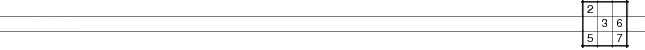
Rule of 21

The Rule of 21 applies to 6 x 6 KenKen puzzles.

It states that any row or column must add up to 21 (1+2+3+4+5+6) and therefore conclusions can be drawn from the overlap of cages. There is also a multiplication equivalent called the Rule of 720.

As of September 2024 the KenKen solver also has the Rule of 42 and considers two adjacent rows or columns and looks for pseudo-cages of up to four cells.

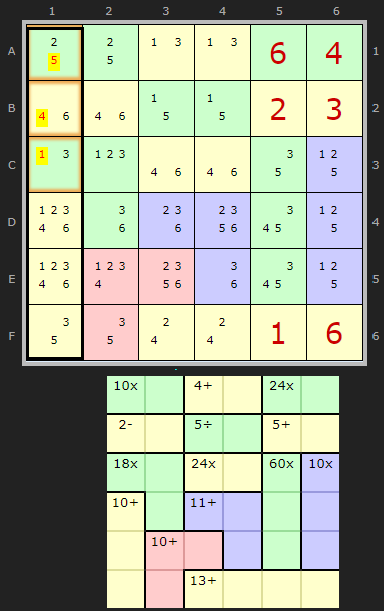
In the first column we have a yellow cage with a 10+ clue. It is entirely within the column. Knowing that the total of the column must be 21 we know 11 remains to be filled in the other cells.

There are three combinations that add up to 11: {1+4+6}, {2+3+6} and {2+4+5}.

Looking at the remaining candidates it is clear that the first and third cannot fit in these cells.

So the combination is {2+3+6}. That means

- 5 can be removed from A1
- 4 can be removed from B1
- 1 can be removed from C1

Load example into solver

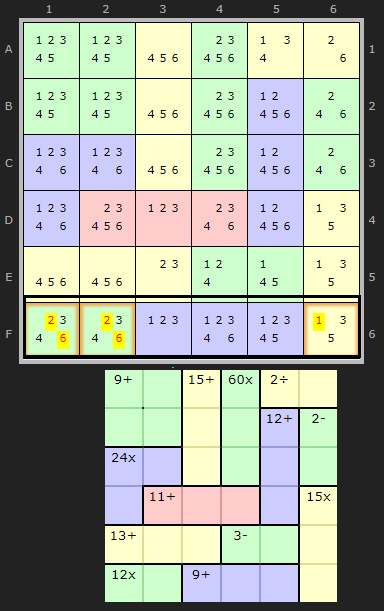
Here is a tough example on a particularly hard bottleneck.

We have 9+ in three cells leaving 12 to fit elsewhere. 12 is a very mid number for 3 cells and the combinations span all six numbers: {1+5+6}, {2+4+6} and {3+4+5}.

So what fits in F1, F2 and F6? 1 and 5 are in the same cell so not the first one. 4 and 6 in two cells byt no 2 in F6 so {3+4+5} it must be. Therefore:

- 2/6 can be removed from F1
- 2/6 can be removed from F2
- 1 can be removed from F6

Load in solver

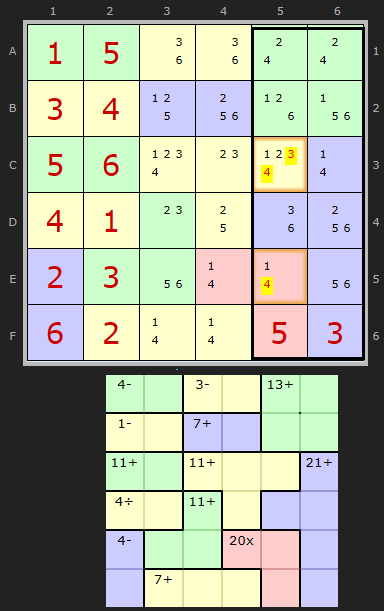
This first example of a Rule of 42 can be loaded here.

We want to add up all the cages wholly inside the last two columns AND use the + operator. No others. These are the green cage with 13 and the blue cage with 21. We ignore the solved cell 3 in F6 since this value is included in the 21. That gives us 13+21 equalling 34. However we do need to include the 5 in F5 to give us 39.

This leaves 3 to fit in 2 cells C5 and E5 which are the remaining cells not totalled up. This is a nice easy example since 42 - 39 = 3. That means 3 must be the sum of C5 and E5. The only combination is 1 and 2 so

- 3/4 can be removed from C5
- 4 can be removed from E5

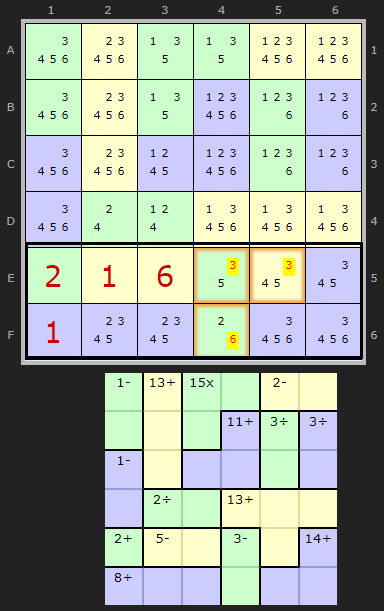
Finally lets end with the example sent in by Roger Taft that inspired this expansion. A puzzle from the kenkenpuzzle.com and their daily from 8th of September 2024.

We are luck a number of things make this possible> yes there are three cages with the + operator, so 2 + 8 + 14. However it would have been a blocker trying to work with the yellow cage with 5- in it. However, we know the solutions to these cage cells, 1 and 6. So ignore the operator and add them to the total to give us 31.

42 - 31 = 11

As in the first example there are three combinations that add up to 11: {1+4+6}, {2+3+6} and {2+4+5} but only the last one fits the remaining canidates. So

- 3 can be removed from E4
- 3 can be removed from E5
- 6 can be removed from F4

Load in solver

Note: the same number can appear in the same cage if the cage "dog-legs" like an L. That means more combinations must matter for Rule of 42 if the pseudo-cage is L shaped. Also, it is possible to end up with a pseudo-cage of 2 cells but they are on different rows and columns. The solver does not have the combinations computed for this situation so this particular scenario is ignored.