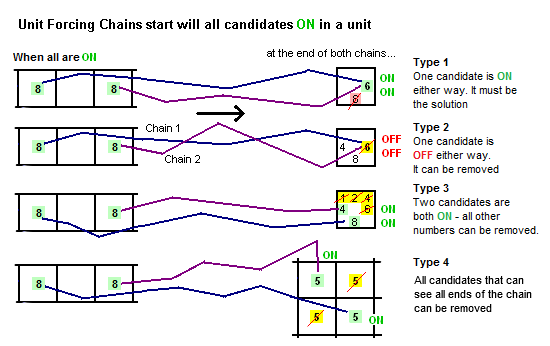
Unit Forcing Chains

If this is your first visit to these strategies, do read the article on Digit Forcing Chains which begins the explanation of this type of strategy and continues to with Cell Forcing Chains. Digit and Cell Forcing Chains are simpler to identify.

If we are forcing a result from a single cell we are obliged to look at all the numbers in that cell. But the logic can be flipped on its head by considering all of X on a unit. If you have three 8s on a row, you know one of those will be the solution. It may be possible to force an elimination by finding a target which can't be true no matter which of those 8s will it turns out to be.

These are the different types of eliminations available from Unit Forcing Chains. The diagram shows part of a row with two candidates but the same types and principles apply to units with three (Triple) or four (Quad) candidates - just add more chains

I do know of some Dual Unit Forcing Chains but they are part of such nightmarish puzzles I don't want to use them for examples. They are pretty rare considering that Alternating Inference Chains are sought after first. So we are going to plunge straight into a Triple.

The example to the right is not too entangled. We have three 5s in box 9 on G9, H7 and J7. If any of these is the solution (and one has to be) we can show that C1 cannot be a 9. The first chain (in blue) in from 5 G9 forcing a 9 in C9 thus turning 9 off in C1.

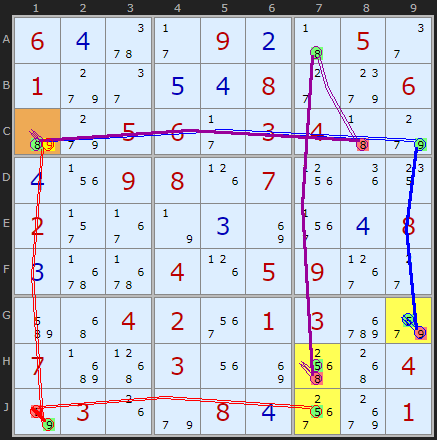
The second chain, purple, from H7 means no 8 in that cell to 8 must be in A7 (strong link) which takes of 8 in C8. Therefore 8 must go in C1 knocking out the 9. It's also a short chain: +5[H7]-8[H7]+8[A7] -8[C8]+8[C1]-9[C1].

The final chain, in red, obliges J1 to be a 9 removing 9 as an option in C1. Quite a clear and short set of inferences.

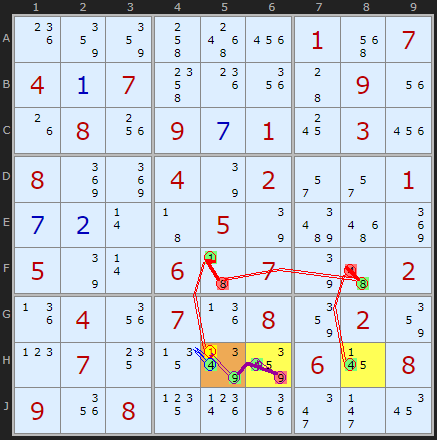
Sometimes the target candidate can be on one of the Unit Forcing Chain cells as it is in this second example. We're looking at the 4s in row H - which occur on H5, H6 and H8. The target is 1 on H5. Just the +4 on H8 has a respectable chain: +4[H8]-4[F8]+8[F8] -8[F5]+1[F5]-1[H55.

The "blue" chains consists of turning the 4 on in H5 which must turn off the 1. The purple chain is next door on and you should be able to trace it.

A recent change (Oct 2025) allows a single digit in a unit to be a "chain" by turning it ON. This has permitted shorter and simpler chains in many instances. Here +5 in G7 is one of the three 5s in column 7. The three chains are the shortest set of chains where we can ask "what 5 can see all the chain ends where 5 in ON. In this case G2 can see D2, G3 and G7.

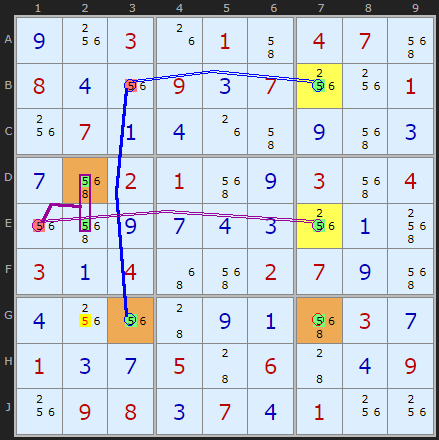
Type 4: All three 5s in Col 7 make chains which end in +5, so candidates that can see all chain ends can be eliminated:
- 5 can be removed from G2

+5[B7]-5[B3]+5[G3]
+5[E7]-5[E1]+5[D2|E2]
+5[G7]

Exemplars

Here are two puzzles found by Klaus Brenner with two Unit Forcing Chains and no other strategies apart from Hidden Singles.

• Exemplar 1, x1 (score 88)
• Exemplar 2, x1 (score 101)