Finned X-Wing
From sudokuwiki.com, the puzzle solver's site
breakline

This is a very subtle yet beautiful extention of logic. We're looking at formations that could potentially be X-Wings but have a corner that's not quite right. In an X-Wing we are looking for four cells in a rectangle which contain a candidate N that exists just twice in either the two rows that form the rectangle or the two columns. Our Finned version is still a rectangle but it has extra candidates of the number in question that prevent one of the two pairs we need from existing.

Let’s look at the distribution of 8 candidates on the board in Figure 1. We have a potential X-Wing marked with the green X. The two blue lines show the top pair of 8s and the potential pair of 8s on the bottom row, F. It’s not a real X-Wing because two cells have gotten in the way. These are the red +8s marked in F8 and F9. If these cells didn’t exist, we’d be able to eliminate 8s in columns 1 and 7 (marked with a red elimination cross).

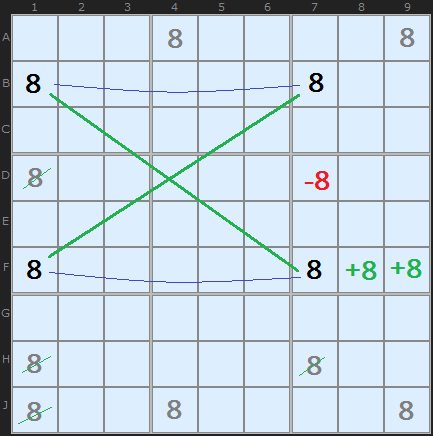
These +8 cells are the “fin”. The “fin” or “fillet” rule goes as follows:

If you can form an X-Wing by ignoring the fin cells, then you can keep your elimination of any cell that shares the same unit as all the cells in the fin.

Finned X-Wing Example

It's important to remember we can only have one fin at a time!
In our example, the -8 is the only cell that shares a box with the +8 cells. It would have been eliminated anyway if the X-Wing were real. However, none of the other X-Wing eliminations are valid.

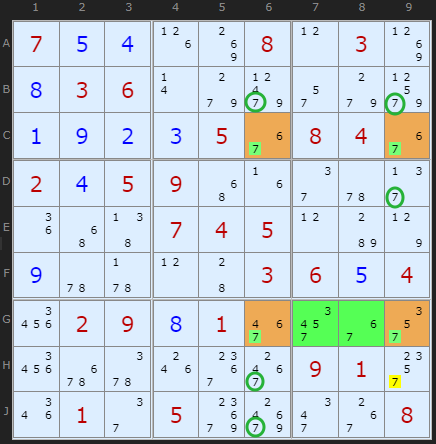
Turning to a real example, consider the potential X-Wing on 7 marked in green in Figure 2. We would dearly like to remove all the 7s marked with a green circle. However, the are extra 7s in box 9, marked in yellow. These are the fin cells. But the fin rule allows us to remove the 7 on H9 at least (red circle).

Finned X-Wing Example: Load Example or : From the Start

Sashimi Finned X-Wings

Now there is more to the idea of Finned X-Wings as I demonstrate in this example.

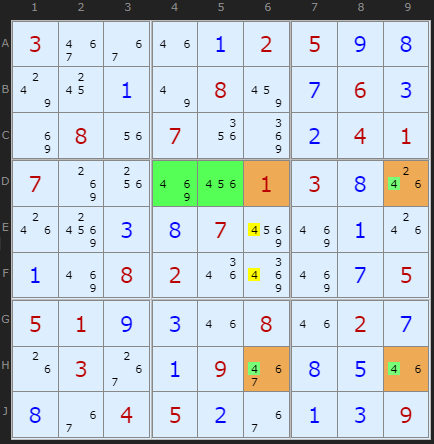
It so happens, that when using the "fin" or “filleting” rule, it is permissible for the X-Wing to be missing a corner in the finned box. The logic can still be applied! It's going to be fun to explain how and why it works, but first lets look at the example on the right.

We are looking at candidate 4. The fin is again marked in yellow but the corner of the X-Wing missing. There is no 4 at D6 - which so happens to be a clue, and therefore was never a candidate 4 there at any time! But it doesn't matter, we can remove the 4s from E6 and F6 because they are in the same box as the fin and the potential X-Wing eliminates in the columns in this example.

Where the Finned X-Wing is missing the candidate in the finned box, the type is called a Sashimi Finned X-Wing.

Sashimi Finned X-Wing: Load Example or : From the Start

It is possible to consider this example in another way. Either there will be a 4 in D9 or there will be a 4 in one of the two cells {D4,D5}. If the later then the 4s in E5/F6 must go (same box situation) or the 4 in D9 forces a chain giving us 6 in H9 and 4 in H6 - which also eliminates the 4s in E5/F6.

However, a more subtle and alternative argument is presented as part of the page on Pattern Overlay Method.

To continue the theme next visit Finned SwordFish.

Comments...

Tuesday 3-Nov-2009

... by: suneet

Despite removing tick mark solver does use this strategy. which normally it should not use in that case. I request you to remove this anomaly
thanks, love your site

Saturday 18-Apr-2009

... by: Roland Zito-Wolf

It's worth mentioning that the finned x-wings can be explained as grouped x-cycles of the rule-3 nice loop variety, the kind with 2 weak links in a row.

For example 1, we have C6=C9-H9-[G7,G8,G9]=G6-C6, allowing 7 at H9 to be removed. This clarifies why the 7 at H9 can be removed but not the ones at J7 and J8: only H9 has a link to C9.

The sashimi variation works because it uses exactly the same kind of grouped x-cycle: H9=H6-E4-[D4,D5]=D9-H9 and likewise for F5.

That raises the question of whether the Swordfish and Jellyfish can be related to more general strategies as well...

love your site!

Add your comments

Article created on 12-April-2008. Views: 12181
This page was last modified on 8-May-2008, at 19:19.
All text is copyright and for personal use only but may be reproduced with the permission of the author.
Copyright Andrew Stuart @ Scanraid Ltd, 2008