Finned Swordfish
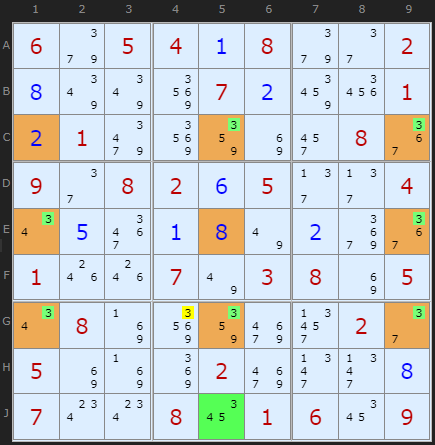
Now, that said it is not a perfect Swordfish because the centre column 5 contains an extra 3 in J5, which ruins the whole formation. However, the Finned Rule says we can ignore it if we confine the eliminations to the box where the fin is, namely box 8. There is one 3 that we can remove, on G4.
Sashimi Variety
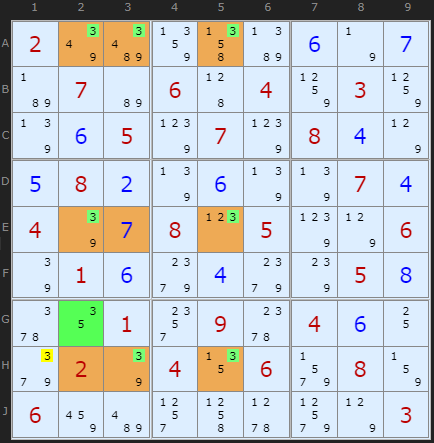
Two examples now of the Sashimi variety of Finned SwordFishies.
Figure two is a little more bunched up but we have a 2-2-3 formation based on eliminations in rows. The exceptional candidate 3 which blocks this from being a perfect SwordFish is on G2. But we can invoke the Sashimi observation to ignore the lack of a 3 on H2, one of the corners of the SwordFish. Eliminating in row H and box 7 we an remove the 3 from H1.
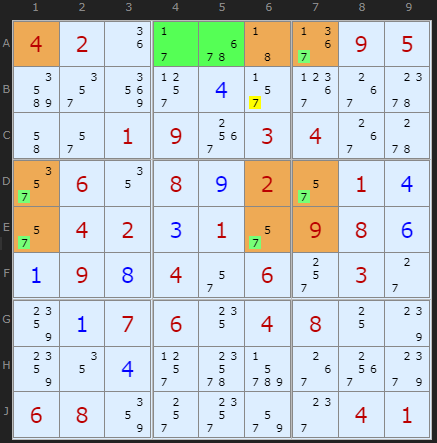
The second example illustrates that the Sashimi cell doesn't have to be a clue or a solved cell. The brown cell A6 simply lacks the candidate 7, which had been removed using previous logical strategies. The double fin is in green, A4 and A5. This is quite a restricted SwordFish, which in row orientation is a 1-2-2 formation - but it works!
(Turn Grouped X-Cycles off)
Here is a lovely Sudoku made by Klaus Brenner (April 2012).
Try loading this one. It contains
Try loading this one. It contains
- 1 X-Wing on 6
- 1 Finned-X-Wing on 6
- 1 Swordfish on 9
- 1 Finned Swordfish on 6, brown cell H9 never contained a 6
- 1 Finned Sashimi Swordfish on 6, brown cell G8 never contained a 6
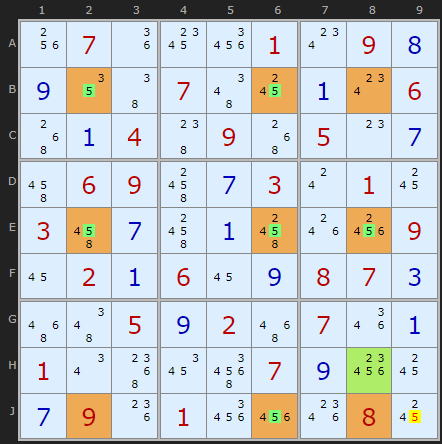
As of August 2025 a slightly more subtle pattern is detected thanks to an old post by Reetou. If the Sashimi ignores the missing X value in one corner then the double Sashimi ignores X in two! I've found a number in my stock. Here is one based on BEJ268. The missing 5s are in J2 and J8. It may be worth checking both boxes for fins and eliminations - if not one then the other.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Robert
On the "Aligned Pair Exclusion" page, I have described a strategy I have implemented in my solver, which I call "dynamic locked sets" - it is a generalisation of the idea of an ALS in an alternating inference chain. Most useful in a forcing net, but it could come up in an AIC as well. I have similarly implemented, within my "forcing net" algorithm, dynamic groups, dynamic finless fish, and dynamic finned fish.
Here are the statistics on how many puzzles in my small database of 245 can be solved using my forcing net software, with its various dynamic options. Every combination is shown, except that there is no easy way to include finned fish without also including unfinned fish.
Basic (no "dynamic" options) - 165
With dynamic groups only - 168
With dynamic locked sets only - 169
With dynamic finless fish only - 167
With dynamic finless fish and dynamic finned fish only - 195
With dynamic groups and dynamic locked sets only - 173
With dynamic groups and dynamic finless fish only - 169
With dynamic groups, dynamic finless fish, and dynamic finned fish only - 203
With dynamic locked sets and dynamic finless fish only - 172
With dynamic locked sets, dynamic finless fish, and dynamic finned fish only - 206
With dynamic groups, dynamic locked sets, and dynamic finless fish only - 173
With dynamic groups, dynamic locked sets, dynamic finless fish, and dynamic finned fish - 209
The final 209 number includes a good number of the "unsolveables", although this technique definitely remains stumped by some other unsolveables.
Granted, 245 is not a huge sample, but based on the results above, I feel like there could be a lot of mileage to be had by incorporating the concept of an "almost (finned) fish" into the AIC algorithm, or its generalisation, a "dynamic (finned) fish" (either in an AIC, or in a general forcing net).
Something to consider :)
... by: dontsaymyid
While solving puzzle
080040070000005800040700020063500002200000005800002760010007030009300000050080010
after some singles and finned X-Wing, puzzle gets into this state:
My solver printed
"Finned Swordfish
On candidate 4. A fish goes from Column 1, 8, and 9 to Row B, D, and G. On Box 6, the fish has two fins E8 and F9. Therefore...
4 taken off from Cell D7."
(Actually this is a sashimi, but it was meaningless to tell sashimi apart from finned one.)
A sashimi swordfish with two non-aligned fins. I used your solver to see how it solves the puzzle, (turned off GXC and ER) but seems like the finned swordfish algorithm does not find this case.
... by: Reetou
While solving puzzle 7.9.........4..2.7.2....3...72......3...17.6.9..2...345347..1.929.........1......
After some other steps, puzzle gets into this state:
There is a sashimi swordfish in rows 2, 6, 7 and columns 3, 5, 6 with fin in r2c2 which eliminates 6 from r3c3.
Am I missing something or just found space for improvement of your solver? Which is brilliant anyway.
... by: Ludi
... by: Rainer
Applying the same logic as in the Finned Sashimi Example 1 to Example 2, I find an 'imperfect' 2-1-2 SwordFish in columns 1, 6 and 7.
Accordingly, A6 in Example 2 has the same role than H2 in Example 1; a cell of the SwordFish that does not contain the candidate.
Thinking in columns the 'fin' would be B6; restricting elimination to the box of the SwordFish, A4 and A5 could be deleted.
The example argues the other way round: A4 and A5 being a 'double fin' and B6 to be deleted!
Where is the fault?