X-Cycles (Part 2)
So far, I been looking at X-Cycles which alternate perfectly all the way round. There are two interesting rules that lead to eliminations when we identify an imperfection in a loop which is called a discontinuity.
A discontinuity occurs when we find two strong links next to each other (that is, with no weak link between them) or two weak links next to each other (with no strong link dividing them). These rules work only if there is exactly one discontinuity, and such a loop will always have an odd number of nodes.
'Discontinuity' doesn't mean that the loop is broken or that it's not chain; it refers only to the imperfection that would otherwise make links alternate strong/weak/strong, and so on.
A discontinuity occurs when we find two strong links next to each other (that is, with no weak link between them) or two weak links next to each other (with no strong link dividing them). These rules work only if there is exactly one discontinuity, and such a loop will always have an odd number of nodes.
'Discontinuity' doesn't mean that the loop is broken or that it's not chain; it refers only to the imperfection that would otherwise make links alternate strong/weak/strong, and so on.
Nice Loops Rule 2
Untick Rectangle Elim : Load Example or : From the Start
If the adjacent links are links with strong inference (solid line), a candidate can be fixed in the cell at the discontinuity.
This rule allows us to know the solution of a certain cell absolutely, no matter how many other candidates there may be on that cell. Unlike the case of the first Nice Loop rule, we are not looking at a mass of eliminations outside the loop; instead, this rule tells us something about the loop itself. Let’s look at an example before examining the logical proof.
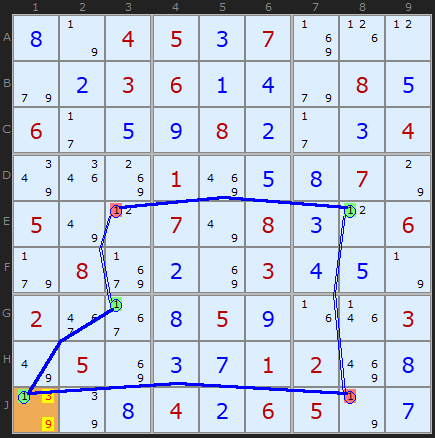
For discontinuous X-Cycles, the notation always starts with the discontinuity. In Figure 1, our Nice Loop on number 1 is:
X-CYCLE on 1 (Discontinuous Alternating Nice Loop, length 6):
-1[J1]+1[G3]-1[E3]+1[E8]-1[J8]+1[J1]
- Contradiction: When 1 is removed from J1 the chain implies it must be 1 - other candidates 3/9 can be removed
We have two strong links joined at J1; therefore, J1 is 1. One way to make sense of this logically is to trace round the alternative. If J1 was not a 1 G3 and J8 would have to be 1s. That would remove the candidate 1 from E3 and oblige E8 to be a 1. But hang on - that forces two 1s in column 8. A contradiction so the 1 must exist in J1.
Nice Loops Rule 3
Our third rule dictates what happens when two weak links form a discontinuity in a loop:If the adjacent links are links with weak inference (broken line), a candidate can be eliminated from the cell at the discontinuity.
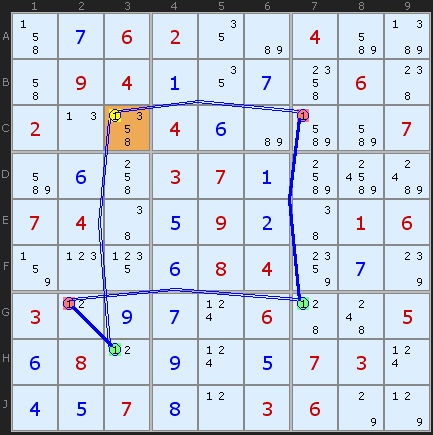
Note: The solver finds a Rectangle Elimination first since that is the simpler pattern. A short example like this may overlap with RE.
The solver would return this message:
X-CYCLE on 1 (Discontinuous Alternating Nice Loop, length 6):
+1[C3]-1[C7]+1[G7]-1[G2]+1[H3]-1[C3]
- Contradiction: When C3 is set to 1 the chain implies it cannot be 1 - it can be removed
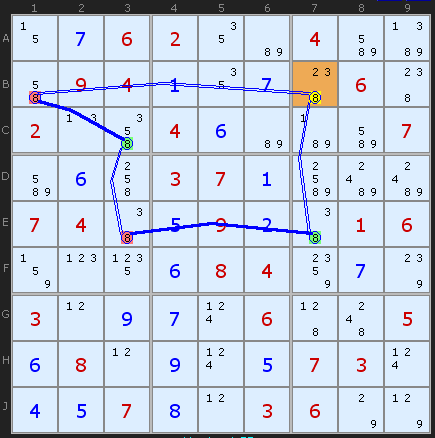
Just a little further on from we have some more AICs including this 8 elimination
Note: this also require RE to be disabled
X-CYCLE on 8 (Discontinuous Alternating Nice Loop, length 6):
+8[B7]-8[B1]+8[C3]-8[E3]+8[E7]-8[B7]
- Contradiction: When B7 is set to 8 the chain implies it cannot be 8 - it can be removed
Weak and Strong Links
X-Cycles introduced the idea of Weak and Strong links but I want to make a more precise definition of terms since there are subtleties which will be useful in other chaining strategies. The rough and ready distinction between Strong and Weak links is to do with how many candidates are in a unit – namely, Strong links are formed when only two are present, while three or more imply a Weak link.
From a strong link we can infer that
if not A, then B
From a weak link, we can infer only that
if A then not B, C, D according to how many candidates there are in a unit
This implies that:
However, the following is also true that for a strong link:
if A, then not B
So, some Strong links can be reversed to give us a "link with weak inference" - if the occasion calls for it. It is perfectly logical to assert on a unit with two candidates of X both:
In Figure 5 we have an array of 6 candidates on a board. A number of strategies can show that the 6 on H9 can be eliminated. I have coloured some cells using Simple Colouring Rule 2 which link up some pairs on the board - either all of the yellow cells will be 6 or all of the cyan cells will be 6. Since H9 can see C9 (yellow) and H5 (cyan) it cannot be a 6 since it can see cells with both colours.
From a strong link we can infer that
if not A, then B
From a weak link, we can infer only that
if A then not B, C, D according to how many candidates there are in a unit
This implies that:
- Strong links are "links with strong inference"; and
- Weak links are "links with weak inference".
However, the following is also true that for a strong link:
if A, then not B
So, some Strong links can be reversed to give us a "link with weak inference" - if the occasion calls for it. It is perfectly logical to assert on a unit with two candidates of X both:
- If Not A then B (!A =>B)
- If A then Not B (A => !B)
In Figure 5 we have an array of 6 candidates on a board. A number of strategies can show that the 6 on H9 can be eliminated. I have coloured some cells using Simple Colouring Rule 2 which link up some pairs on the board - either all of the yellow cells will be 6 or all of the cyan cells will be 6. Since H9 can see C9 (yellow) and H5 (cyan) it cannot be a 6 since it can see cells with both colours.
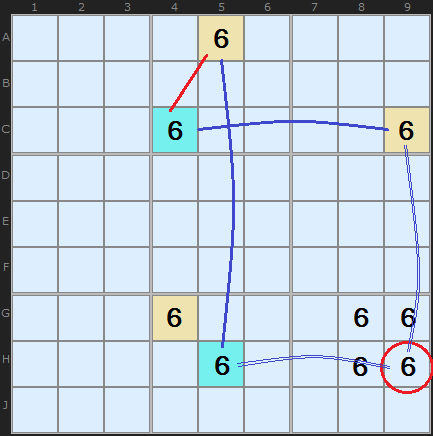
If a strong link can have weak inference, then let’s just change the link from C4 to A5 to imply such. Simple. We get our pattern. If 6 is on C4, then it is not on A5 (weak inference), or if it is on A5, then it is not on C4 (also weak inference – and all very logical).
I have coloured the Strong link with weak inference red in Figure 5.
X-Cycle Exemplars
These puzzles require the X-Cycle strategy at some point but are otherwise trivial.They also require just one Naked Pair.
They make good practice puzzles.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: natalie
... by: rrobert
... by: Ymiros
What confused me most when reading this article was the question why these chains have to be alternating, what exactly that implies and what the point of viewing strong links as quasi weak is (I still don't think there's a point to this as I will explain later).
I personally was able to get a much better grasp of this by think of ON and OFF as different elevations, I will call them 0 and 1, 0 being on the ground and 1 being elevated. Then you have strong links as stairs that you can climb up or down (A => !B and !A => B) while weak links are slides that you can only go down, but not up (A => !B).
In the examples I will try to illustrate this on I will use \ for a slide (weak link) going down and ↗ and ↘ for stairs (strong links) going up or down respectively. For a chain in its base state I will use - for strong and = for weak links.
Thus a nice loop could look something like this: A-B=C-D=A, forming a closed alternating chain with 4 members.
Now we could assume A to be elevated and go right: A1↘B0, however we are now stuck since we are at the bottom of a slide and can't go beyond it, so let's go the other direction: A1\D0↗C1\B0↗A1. This is a nice working loop, let's try the other option where A is 0 too. If go in the same direction, we will come to a halt right away as we start at the bottom of a slide, so we have to go the other way: A0↗B1\C0↗D1\A0. As we can see everything has been exactly inverted by just inverting A, but the strong links still always go up and the weak links always go down. Obviously a strong link could also do the job of a weak link here, but as it still always goes down you could call it a quasi-weak link.
This pattern will obviously work for chains of any even length, but what exactly happens if we switch it up?
Let's look at having 2 strong links in a row: A-B-C.
Option 1: A1↘B0↗C1
Option 2: A0↗B1↘C0
As you can see A and C are always the same. Thus if we have 2 strong links in a row we can just treat them as not being there and instead the ends being the same. Eg A-B=C-D-E=A would simply become A-B=C=A. This separates chains of consecutive strong links in just 2 cases: An odd amount that is equivalent to 1 strong link and an even amount that is equivalent to both ends being one cell.
Now let's look at 2 weak links in a row: A=B=C
Option 1: A1\B0
Option 2: A0
Turns out 2 links in a row kill information very quickly, if you arrive at the chain with 0 you can't even traverse the first link and if you arrive with 1 you still fail at the second, because that one then is 0.
But if the chain is looped we can gain a little more information as long as that chain allows to propagate information properly in both directions, eg: A=B=C-A
Option 1: A1\B0
Option 2: A0↗C1\B0
We see that as either one or the other end always has to be 1, B has to be 0.
(Another way to see this is if you set B to 1 both A and C have to be 0, which is a contradiction.)
Obviously any additional disruption in the chain won't allow this conclusion as you have to be able to go around the chain from one end of the 2 weak links to the other.
It is obvious that more weak links in a row will simply get rid of any and all information as even if you know either end has to be 1 you don't know anything about the middle digits.
So we can extend the definition of an alternating chain to one where weak links are separated by not exactly 1, but an odd number of strong links (Since remember, any even number of strong links is the same as no strong link).
Also we can define an discontinuity as 2 weak links separated by an even number of strong links, since we saw that information cannot propagate through to weak links in a row and again the 0 strong links between the 2 weak ones are the same as any even amount of strong ones.
The condition of an odd number of links automatically results from the condition of there being no more than one discontinuity (As you cannot go past a continuity you wouldn't be able to go from one end to the other of the same discontinuity, rendering it useless) since if there was an even number you would get a second discontinuity (I hope this is obvious, for this to not be the case you would need a continuous alternating chain with an even number of links and a strong link on both ends, which is impossible).
Thus I don't exactly agree with Robert that rule 3 encompasses rule 2 or anything, rather that they're actually both exactly the same as 0 and 2 strong links within the discontinuity are exactly the same as discussed above.
Also while I said that the rule about an odd number of links in total follows automatically I think it should be made more prominent on the page since imo it is pretty easy to spot how many links there are in total and if the number is even you don't even need to bother looking for a discontinuity.
... by: Anonymous
... by: Ed Logg
5.9..8.14...9..53.3..25.987.5.1..8.....4851791...2.45.8..5..7.1.156.73.8.7.81..95
When you remove 2 & 4 at G8, you can also remove the 2 at A7!
... by: Robert
I have recently discovered this fascinating website, and found it immensely useful. I have written my own software, and am continuing to improve it, more for my own understanding than any other reason.
It seems to me that the x-cycles with two consecutive weak links subsumes the other two cases. If you have two consecutive strong links, just let one of them be "pseudo-weak", then there are two consecutive weak links. Together with "last cell in a unit", this gets you as much inference as the two consecutive strong-link case.
An x-cycle with alternating strong-weak links (no discontinuity) can also be used as a special case. With this type of loop, you can eliminate the value from any cell with links to a "red" or "green" cell in the loop. But we can just construct a loop that goes from the "red" cell to the one that is off the loop, back to the "green" cell, then around the loop in one direction or the other. In one of the two directions, this leads to a loop with an odd number of links, and two consecutive weak links (or strong links that can be treated as weak). The "off loop" cell is the one that is between the two weak (or pseudo-weak) links. So the value is eliminated from this cell, which is the same thing that happens if we use the loop with the even number of links, alternating strong and weak.
I have also convinced myself that the stipulation in the text, that no cell occurs in the loop twice (I started to picture such a configuration as a "figure eight") is not restrictive - any such configuration can be broken into two loops, and together with "only value in a cell" or "only cell in a unit", we get at least as much inference from the two sub-loops as we do from the "figure eight" loop. So not allowing a cell to occur twice costs us nothing.
I cannot convince myself that it is possible to ignore loops where there are links between non-consecutive cells. Such loops could also be broken into distinct sub-loops, but it seems to me in some cases, you do not get the same inference from the two sub-loops that you get from the overall loop.
The x-loop with two consecutive weak links also would seem to completely subsume the two rules of the simple chain strategy.
How does all that sound?
Great work, glad I came across this site!
... by: David Añez
-8[J4]+8[H5]-8[B5]+8[B2]-8[F2]+8[F3]-8[J3]+8[J4]
while I find first the chain
+8[A4]-8[B5]+8[B2]-8[F2]+8[F3]-8[J3]+8[J4]-8[A4]
The end result is kind of the same. My chain removes 8 from A4, while your chain sets 8 in J4, which removes it from every visible cell, including A4 (same column)
The only actual difference is that yours is more effective: C4 still has a 8 candidate in my case, so my chain generator actually have to find a second chain to remove it, and then J4 can be established as having 8 as value.
Do you actually enforce CW/ACW chains? Or prefer chains of the same length that are more effective? Setting a value in a cell, as in this case, is more valuable that just removing a candidate.
Also, is there a reason why the name Exemplar is used? English is my second language, and for a while I thought it was a mispelling
... by: John N
... by: YBB
... by: Lou Maser
... by: megmrl1
... by: djinks
... by: Eric
Another way to overcome your problem is simply a redefinition of the X-Cycle requirements: An X-Cycle is a series of links hopping from one candidate to another, where at least an alternate series of strong links exist. I am afraid this might be a bit too theoretical, so I suggest you just forget about the stong link in box 2.
... by: roger freeman
In 'x-cycles pt2'/nice loop rule3/fig2, concerning elimination of candidate 3 in cellB6, where two weak links converge; can this loop be routed thro cellC6 and therefore allow that candidate 3 also be eliminated in cellC6.
Sorry if I'm being v silly. If another loop thro' cellC6 and elimination of
candidate3 at that cell is not legitimate, could you explain please.
I feel fearful of serious confusion!
Many thanks indeed for your site.
Bests,Roger Freeman
Corbridge,Northumberland
... by: Gary Maness
!A=>B ~ A=!B
But not all weak inferences are strong ones,
A=>!B !~ !A=B.
Am I right? I think I remember proving this in my foundations of Mathematics course.
... by: patriotkiller18