 |
 |
| Print Version |  |
| Solvers |
| Puzzles |
| Basic Strategies |
| Tough Strategies |
| Diabolical Strategies |
| Extreme Strategies |
| Depreciated Strategies |
| Str8ts |
| Other |
|
 Order Now! |
 Order Now! |
This is a very subtle yet beautiful extension of logic. We're looking at formations that could potentially be X-Wings but have a corner that's not quite right. In an X-Wing we are looking for four cells in a rectangle which contain a candidate N that exists just twice in either the two rows that form the rectangle or the two columns. Our Finned version is still a rectangle but it has extra candidates of the number in question that prevent one of the two pairs we need from existing.
Let’s look at the distribution of 8 candidates on the board in Figure 1. We have a potential X-Wing marked with the green X. The two blue lines show the top pair of 8s and the potential pair of 8s on the bottom row, F. It’s not a real X-Wing because two cells have gotten in the way. These are the green +8s marked in F8 and F9. If these cells didn’t exist, we’d be able to eliminate 8s in columns 1 and 7 (marked with a green strike-out line). 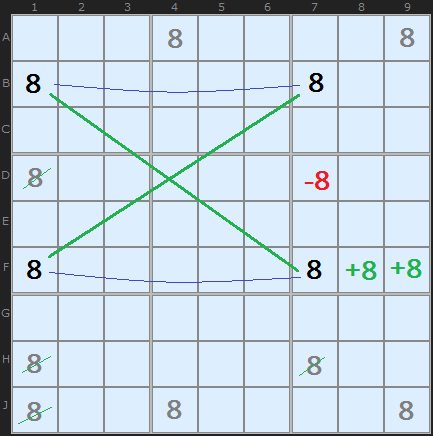These +8 cells are the “fin”. The “fin” or “fillet” rule goes as follows: If you can form an X-Wing by ignoring the fin cells, then you can keep your elimination of any cell that shares the same unit as all the cells in the fin. |
 Finned X-Wing Example |
In our example, the -8 is the only cell that shares a box with the +8 cells. It would have been eliminated anyway if the X-Wing were real. However, none of the other X-Wing eliminations are valid.
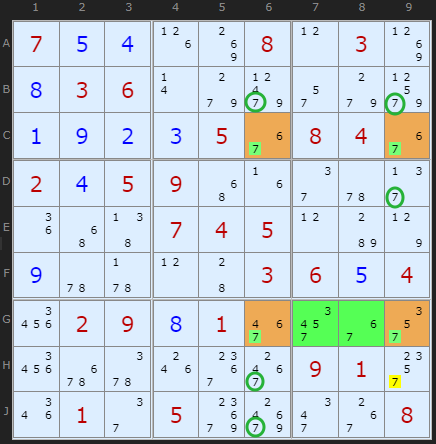
| Turning to a real example, consider the potential X-Wing on 7 marked in yellow in Figure 2. We would dearly like to remove all the 7s marked with a green circle. However, the are extra 7s in box 9, marked in green. These are the fin cells. But the fin rule allows us to remove the 7 on H9 at least (red circle). |
 Finned X-Wing Example: Load Example or : From the Start |
Sashimi Finned X-Wings
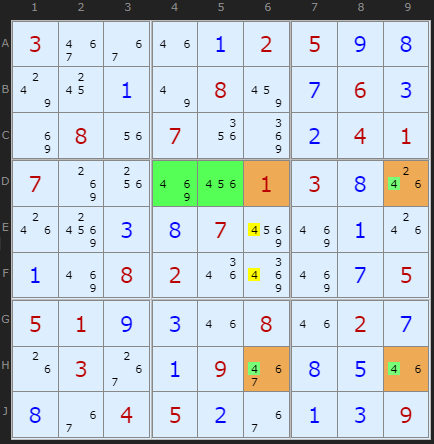
| Now there is more to the idea of Finned X-Wings as I demonstrate in this example. It so happens, that when using the "fin" or “filleting” rule, it is permissible for the X-Wing to be missing a corner in the finned box. The logic can still be applied! It's going to be fun to explain how and why it works, but first lets look at the example on the right. We are looking at candidate 4. The fin is again marked in green but the corner of the X-Wing missing. There is no 4 at D6 - which so happens to be a clue, and therefore was never a candidate 4 there at any time! But it doesn't matter, we can remove the 4s from E6 and F6 because they are in the same box as the fin and the potential X-Wing eliminates in the columns in this example. Where the Finned X-Wing is missing the candidate in the finned box, the type is called a Sashimi Finned X-Wing. |
 Sashimi Finned X-Wing: Load Example or : From the Start |