 |
 |
| Print Version |  |
| Solvers |
| Puzzles |
| Basic Strategies |
| Tough Strategies |
| Diabolical Strategies |
| Extreme Strategies |
| Depreciated Strategies |
| Str8ts |
| Other |
|
 Order Now! |
 Order Now! |
Grouped nodes were discussed on the Grouped X-Cycles page and it is very relevant to Alternating Inference Chains. Luckily, there’s nothing too scary about them although they may be harder to spot.
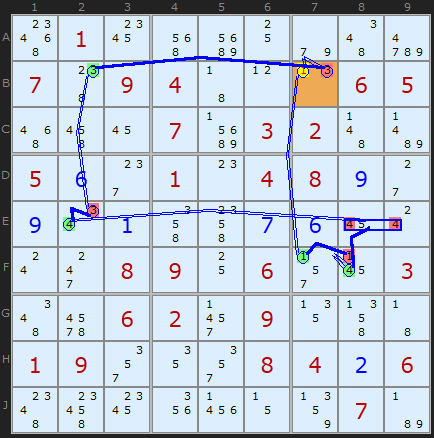
The example on the right shows a classic and relatively simple deduction based on a loop that is predominantly candidates 3 and 4. But the two bi-value cells E8 and E9 containing 4/5 and 2/4 allow us to form strong links that continue the number 4 we’re tracing from E2 to F8. We end up with two weak links pointing to B7, where the 1 can be removed, thanks to Nice Loop Rule 3. Our grouped node on [E8|E9] acts just as a normal cell. The solver gives us: AIC on 1 (Grouped Discontinuous Alternating Nice Loop, length 10): +1[B7]-3[B7]+3[B2]-3[E2]+4[E2] -4[E8|E9]+4[F8]-1[F8]+1[F7]-1[B7] - Contradiction: When B7 is set to 1 the chain implies it cannot be 1 - it can be removed |
 Grouped AIC: Load Example or : From the Start |
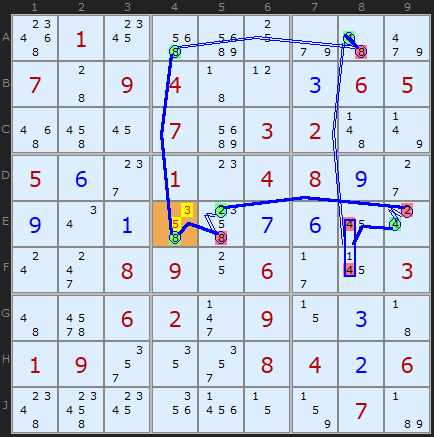
| Just a few steps later in this puzzle we get another AIC which shows Rule 2 - two strong links - which allows us to place with certainty 8 on E4. AIC on 8 (Grouped Discontinuous Alternating Nice Loop, length 10): -8[E4]+8[A4]-8[A8]+4[A8]-4[E8|F8] +4[E9]-2[E9]+2[E5]-8[E5]+8[E4] - Contradiction: When 8 is removed from E4 the chain implies it must be 8 - other candidates 3/5 can be removed |
 Grouped Cell AIC: Load Example or : From the Start |