Death Blossom
(a.k.a. Aligned ALS Exclusion)
This strategy is based on extending Aligned Pair Exclusion but uses Almost Locked Sets to make some clever reductions. From the components used it could be named Aligned ALS Exclusion but Mike Barker, who formulated it first in this thread, hit on "Death Blossom" because it starts with a cell designated as the "stem" which points to Almost Locked Sets, or the "petals", and is a great deal more flowery.
An Almost Locked Set is any group of N cells (that can all see each other) with N+1 candidates between them . This includes bi-value cells. A Locked Set, by contrast, contains exactly the right number of candidates for the group, examples of which are Naked Pairs and Triples.
This strategy is based on extending Aligned Pair Exclusion but uses Almost Locked Sets to make some clever reductions. From the components used it could be named Aligned ALS Exclusion but Mike Barker, who formulated it first in this thread, hit on "Death Blossom" because it starts with a cell designated as the "stem" which points to Almost Locked Sets, or the "petals", and is a great deal more flowery.
An Almost Locked Set is any group of N cells (that can all see each other) with N+1 candidates between them . This includes bi-value cells. A Locked Set, by contrast, contains exactly the right number of candidates for the group, examples of which are Naked Pairs and Triples.
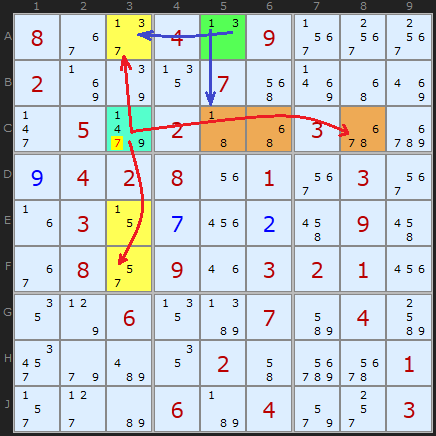
Reversing direction will help illuminate the Death Blossom idea since we start with green “stem” cell. A5 with {1/3} must be able to see at least two ALSs which contain all its candidates. It is important that the 3 in A5 can see all of the 3’s in the yellow coloured ALS and the 1 in A5 can see all of the 1’s in the brown coloured ALS (one instance each in this case). But A5 overall does not have to see every single cell in all the ALSs, just the cells it shares candidates with.
Now, the two ALSs must have a candidate Z in common which the "stem" cell does not have. Because ALSs contain exactly one extra candidate for the number of cells they occupy (the N+1 candidates for N cells rule), we can assert that ANY cell that can see all the Zs in both ALS but is not part of those ALSs or the stem cell can be removed. Such a cell is C3.
Death Blossom was discovered by extending Aligned Pair Exclusion (APE) and asking if there was generalisation beyond the pairs and triples discussed in Aligned Pair Exclusion. With Almost Locked Sets there is. The stem cell A5 and the elimination cell C3 can’t see each other – they not aligned, but the pairs they can make do affect the board. In our example, consider the pairs that can be made between the 7 in C3 and the 1/3 in A5. These are 1/7 and 3/7 in C3 and A5 respectively. Both these turn out to be illegal since they would reduce our ALSs to having less candidates than cells. So whatever the solutions to the two disparate cells C3 and A5, C3 will never contain a 7.
Death Blossom was discovered by extending Aligned Pair Exclusion (APE) and asking if there was generalisation beyond the pairs and triples discussed in Aligned Pair Exclusion. With Almost Locked Sets there is. The stem cell A5 and the elimination cell C3 can’t see each other – they not aligned, but the pairs they can make do affect the board. In our example, consider the pairs that can be made between the 7 in C3 and the 1/3 in A5. These are 1/7 and 3/7 in C3 and A5 respectively. Both these turn out to be illegal since they would reduce our ALSs to having less candidates than cells. So whatever the solutions to the two disparate cells C3 and A5, C3 will never contain a 7.
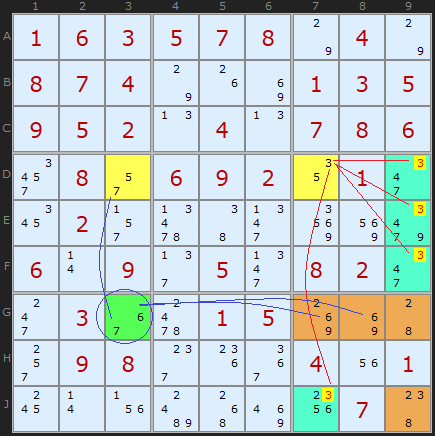
There is another way to look at this example which mirrors some strategies already covered. Starting in G3
If G3 is 7 -> D3=5 -> D7=3 therefore D9,E9,F9,J7 <> 3
If G3 is 6 -> G8=9 -> G7=2 -> G9=8 -> J9=3 therefore D9,E9,F9,J7 <> 3
Much of the first-sight complexity seems to evaporate when traced through in this manner.
Note: Example 2 cannot be found by the solver unless Digit, Cell and Unit Forcing Chains are turned off. I retain it as an example because it's the best one to show multiple eliminations. Indeed 4 eliminations is a pretty good hit. Unfortunately I can't find the orginal Sudoku to give a start position.
Note: Example 2 cannot be found by the solver unless Digit, Cell and Unit Forcing Chains are turned off. I retain it as an example because it's the best one to show multiple eliminations. Indeed 4 eliminations is a pretty good hit. Unfortunately I can't find the orginal Sudoku to give a start position.
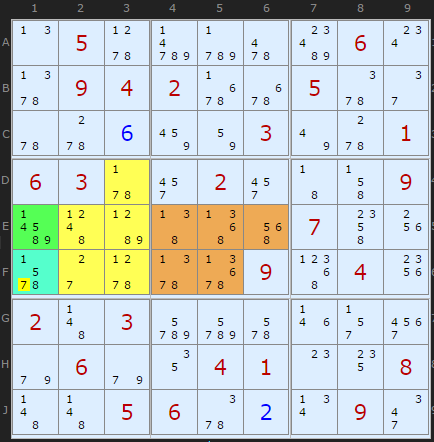
Here is a fun one by Klaus: two massive ALSs in a DB puzzle in only 2 boxes.
Death Blossom
(ALS:{D3|E2|E3|F2|F3} and ALS:{E4|E5|E6|F4|F5}) + Stem:E1 means 7 can be removed from F1
Update August 2013:
Other fun examples Klaus Brenner has found include a Death Blossom with six eliminations and a Death Blossom with all its ALS in only one Box.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Ghost 2T
It was born just to mess up the brain and waste the player's time. (except for the "Death blossom" pattern I see appearing outside of this web, because it has an overlap of hidden Z)
... by: Ghost 2T
Why do u repeat this skills with other name??
Looking at the last image:
- ALS 1: 1245789
- ALS 2: 135678
- RCC=5, Z=7
Remove 7 at r6c1!
(The image 1 & 2: skill the loop +ALS)
... by: JONATHAN HANDOJO
I have yet to find one though, even though it's a nice logic and want to get one so badly... The best I've ever found is ALS, and whenever I use your solver, Aligned Pair Exclusion always picks it up first, haha.
... by: Joe Bleau
You wrote :
“Klaus Brenner has found a Death Blossom with five eliminations”
If I’m right, there are 6 elimitaions.
Here are the 5 found by your program :
Death Blossom
([ALS:F6] and [ALS:E6|E7|E9]) + Stem:F7 means 4 can be removed from B6
([ALS:F6] and [ALS:E6|E7|E9]) + Stem:F7 means 4 can be removed from D4
([ALS:F6] and [ALS:E6|E7|E9]) + Stem:F7 means 4 can be removed from D5
([ALS:F6] and [ALS:E6|E7|E9]) + Stem:F7 means 4 can be removed from E4
([ALS:F6] and [ALS:E6|E7|E9]) + Stem:F7 means 4 can be removed from G6
I think we can add this one :
([ALS:F6] and [ALS:E6|E7|E9]) + Stem:F7 means 4 can be removed from F4
I have a rule in the solver that says any elimination cell can't see the stem cell. But reviewing the example and definitions I am wondering if this is a necessary rule. Removing it I get your 6th. It will take some time to test for a negative as DBs are very rare, being at the end of the strategy list. But I'll give it a go
Edit: released a version with this rule relaxed, seems harmless to do so. Now finds six
... by: last1x {rus}
... by: Thinkist
Update: 25 March 2012. I've replaced the first example with one of those four.
... by: Bud Nienhaus
... by: STRMCKR
THERE IS A TYPO in the first reference cell G8.
it should read G9.