Pattern Overlay
As of July 2024 I've improved the way the POM result is displayed. Gone are the yellow cells which didn't really explain much. Instead we have nice lines tracing the paths.
Invented by Myth Jellies, this strategy looks at the way candidates of a specific digit N can be distributed in the remaining spaces. Every time a digit is placed it removes other spaces in the rest of the row, column and box, quickly narrowing down the possibilities. It is a strategy you don't want to apply too early in the puzzle since the number of overlays might be too large, but in the middle and end games it is fairly easy to apply.
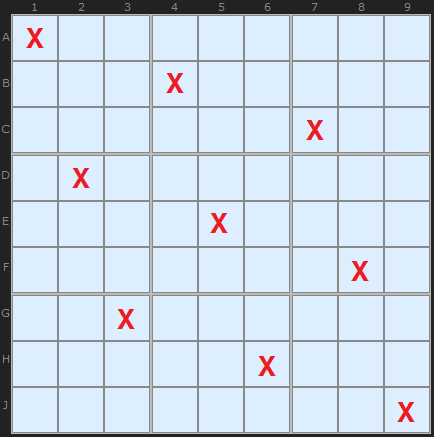
The first diagram shows a possible pattern or template. It is in fact the first such pattern given an empty board and placement from top left to bottom right. On an empty board there are 46,656 different patterns which is why we use this when most cells are filled.
We get this number in the following way (by row or column - doesn't matter):
9 positions in row A
6 remaining positions in row B
3 remaining positions in row C
6 remaining positions in row D
4 remaining positions in row E
2 remaining positions in row F
3 remaining positions in row G
2 remaining positions in row H
1 remaining position in row J
So, 9 * 6 * 3 * 6 * 4 * 2 * 3 * 2 * 1 = 46,656.
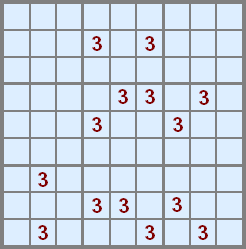
In this relatively simple example all the 3s are shown. We can start from the top block which contains just two threes, so the total number of overlays will be two.
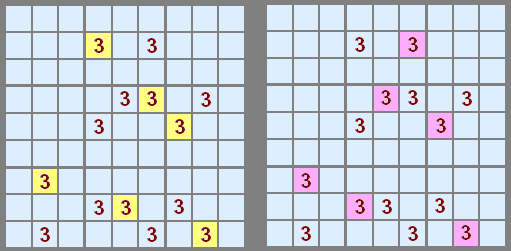
The solver will return one of two types of elimination sets, which it calls "Rule 1" and "Rule 2"
Rule 1 considers each number in isolation. When looking for all the possible patterns for X it is possible that X may not appear in any pattern at all. If found, the solver reports and quits.
Rule 2 looks at all the patterns for all numbers 1 to 9. Within in each number all patterns may want to occupy certain cells - like a bottleneck. If that is the case then those cells are not available for other patterns used by other numbers. This is more cumbersome for a human to calculate, admittedly, but it works very well for the solver and we get a lot of this type. Patterns are pruned down and then Rule 1 is executed to find the first X where cells not used by X. Only the first X is reported - there may be other eliminations from numbers higher than X but it would be too confusing to report the total overlap.
The logic of POM ensure that there will always be at least one pattern for every X despite all these operations - unless the puzzle itself is faulty.
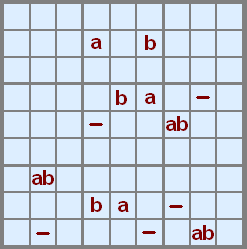
Rule 1 example
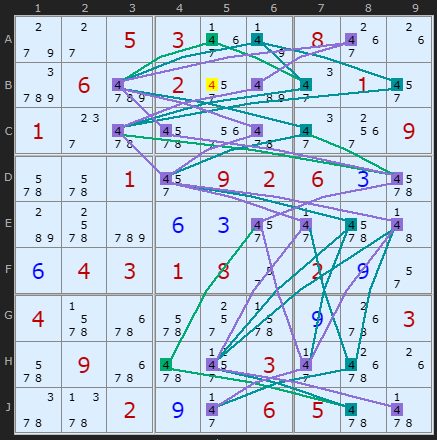
The examples here are from extremely difficult puzzles but that is only because POM is so far down the strategy order. You will find more if you uncheck most extremes.
Starting with a Rule 1 example. This only have three paths for number 4 so it is relatively sparse. Many examples you'll find will have more messy patterns so this one is a decent example. It is a bit hard with the two green colours but still just about possible to trace any valid path and see that the 4 in B5 never gets used.
Rule 2 example
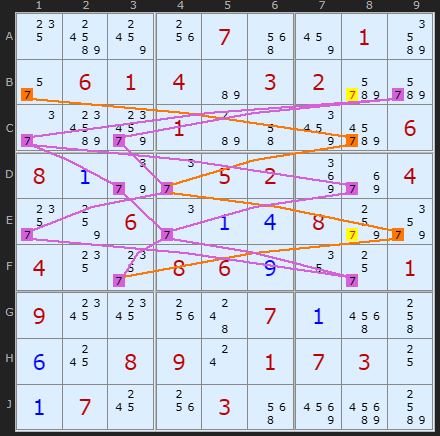
Here is a nice sparse POM on number 7. There are only two alternative paths from B1 and B9. However Rule 2 makes it a bit more difficult to trace since the solver has looked at all the other numbers and found which 7s would be blocked. This blocking leave the two remaining paths shown here and the eliminations that can be made on B8 and E8
Jigsaw multiple example
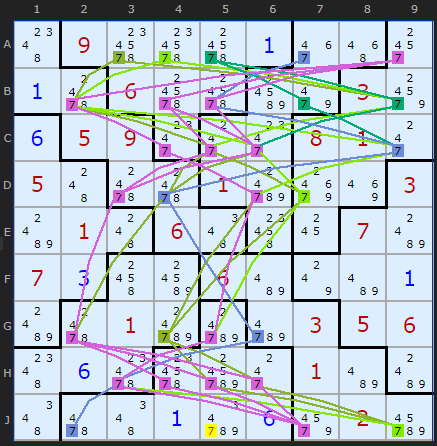
Just to show that POM is equally, if not more applicable to Sudoku variants, here is a Jigsaw with eight POM instances.
At this point we're attaching the 7 in J5 with rule 1 because of all the possible paths for 7.
Pattern Overlay
RULE 1: J5 cannot contain 7,
no pattern uses this cell
Rule 1 considers just the
number 7

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Valery
I am truly impressed by your work on this site. I am learning from you and trying to create my own solver. I have managed to implement the Pattern Overlay strategy according to Rule 1, i.e., removing and setting the sole candidate.
However, I am unable to implement Rule 2, in which the number of candidate patterns is reduced through the use of other candidates.
Would you be so kind as to spare some of your valuable time and explain in more detail, using a concrete example, how this works?
I would be very grateful to you!
So I’ve looked at my code again – been awhile. I’m computing all the overlays for each number. I hold them in strings with defaulting to 000000000 and I need 9 for each number and 9 for each row (third index) so
This is big chunk of memory 27k which I malloc in and free after.
So you have to compute all the overlays for all numbers. Then for each number check if any other overlay requires certain rows. Then remove that from other number overlays. Then you are applying Rule 1 to the what’s left. Not to horrible compute-wise especially compared to AICs so I haven’t optimised it further.
Hope that helps a bit. Let me know how you get on
... by: dontsaymyid
Bowman's Bingo required 3 times : E5 is not 2, J1 is not 3, and D4 is 4.
POM will appear after first bingo.
2024: Need to investigate why this is no longer working as an example
... by: Juan
The unique result I get is r7c3 but is pretty obvious by other methods
... by: Benjedi420vt
Ben
... by: Benjedi420vt
In order for this strategy to be used by a human being and not involve guessing, you need to be able to find both patterns which I cannot figure out how to do in this case. A computer can quickly guess at a couple of the sticky points until it finds a fault and then use the other value as true to find all the patterns...but at that point it's just guessing anyway so why not just use a brute math calculation.
Maybe I'm just missing an easy to see reduction but in the case of a tutorial I believe it should be easy to see and pointed out so all reasonable users can see.
Thanks
Ben
... by: David Spector
PS: I didn't enter the code correctly, even though I am sighted. Probably I have to push the Caps key?
I apologize that my comments are not relevant to the article. This is frustrating for me.
I really dislike CAPTCHA but I had to add it to prevent robotic spamming. It was quite a problem. This one is home grown so I don't have a speaker feature. I can see that will be a problem for blind or partially blind. I'll see what I can find on the internet to replace it. BTW, the code entry field auto-captializes.
... by: S.H.Khatami
I am looking the reference of Myth jellies in Pattern overlaying method. Could you send me this, please. I am writing a book and need that reference.
Dr.S.H.Khatami
... by: ralph maier
Actually at all the points where the 2 patterns overlap G2 J8 and E6 3 is the solution
... by: Anton Delprado
Also in the example G2 is a hidden single in Row G.