Unique Rectangles
Unique Rectangles takes advantage of the fact that published Sudokus have only one solution. If your Sudoku source does not guarantee this then this strategy will not work. But it is very powerful and there are quite a few interesting variants.
Credits first: The initial ideas for these strategies I lifted wholesale from MadOverLord's description (11 Jun 05) on the forum at www.sudoku.com. (Sadly the thread is no longer hosted). Many others have since added to and improved them. I have provided my own examples. (please email me for other credit requests). I will stick to MadOverLord's nomenclature.
Credits first: The initial ideas for these strategies I lifted wholesale from MadOverLord's description (11 Jun 05) on the forum at www.sudoku.com. (Sadly the thread is no longer hosted). Many others have since added to and improved them. I have provided my own examples. (please email me for other credit requests). I will stick to MadOverLord's nomenclature.
 27th January 2025
27th January 2025
Added the ability to cycle through all Unique Rectangles found when the first is displayed.
Similar to how chains can cycle.
Noticing the 'Deadly Pattern'
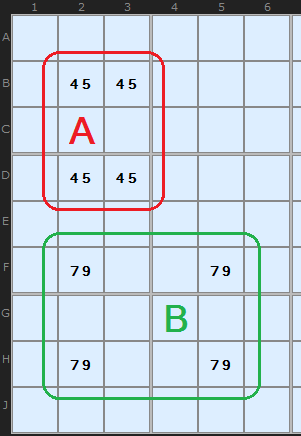
The pattern ringed in green looks like a deadly pattern but there is a crucial difference. The 7/9 still resides on two rows and two columns, but instead of two boxes it is spread over four boxes. Now, such a situation is fine since you can't guarantee that swapping the 7 and 9 in an alternate manner will produce two valid Sudokus. One of them is the real solution, the other a mess. Why? Swapping the 7 and 9 around places them in different boxes and 1 to 9 must exist in each box only once. In the red example, swapping within the box does not change the content of that box.
Type 1 Unique Rectangles
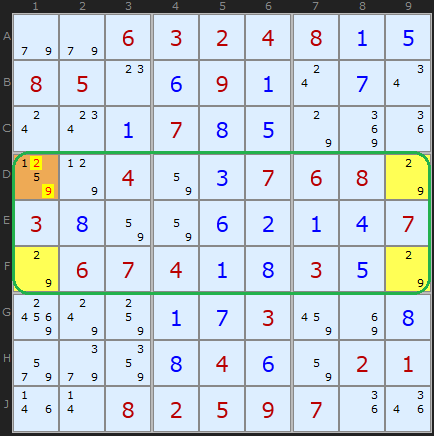
The proof is pretty straightforward once you get your head around the basic idea. Assume D1 is 2. That forces D9 to be 9, F9 to be 2, and F1 to be 9. That's the deadly pattern; you can swap the 2's and 9's and the puzzle still can be filled in. So if the Sudoku is valid, D1 cannot be 2. The exact same logic applies if you assume D1 is 9.
So D1 can't be a 2, and can't be a 9
- it must be either 1 or 5.
Type 2 Unique Rectangles
In Figure 3 we have a similar pattern, but this time, A5 and A6 (cells which are also in the same box) both have a single extra possibility - in this case, 7.
To make subsequent discussion easier to follow, we will refer to the two squares that only have two possibilities as the floor squares (because they form the foundation of the Unique Rectangle); the other two squares, with extra possibilities shall be called the roof squares.
To make subsequent discussion easier to follow, we will refer to the two squares that only have two possibilities as the floor squares (because they form the foundation of the Unique Rectangle); the other two squares, with extra possibilities shall be called the roof squares.
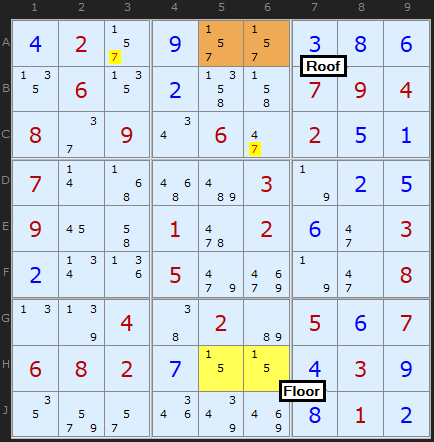
Now that you've gotten your head around the basic unique rectangle concept, the proof should come clear:
If neither A5 or A6 contains an 7, then they both become cells with possibilities 1/5. This results in the deadly pattern - so one of those cells must be the 7, and none of the other squares in the intersecting units can contain 7. So A3 and C6 can have 7 removed. This cracks the Sudoku.
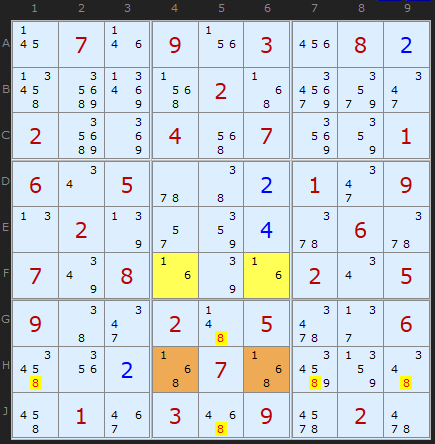
I couldn't resist adding this example which I found while looking for Empty Rectangles. It's as clear as day how the 8s in H4 and H6 combine with the [1,6] Deadly Pattern. 8's aligned with the brown cells are eliminated. I need say no more.
To view this puzzle in the solver uncheck Rectangle Elimination and choose the second Unique Rectangle after the Type 5 which is found first.
Type 2B Unique Rectangles
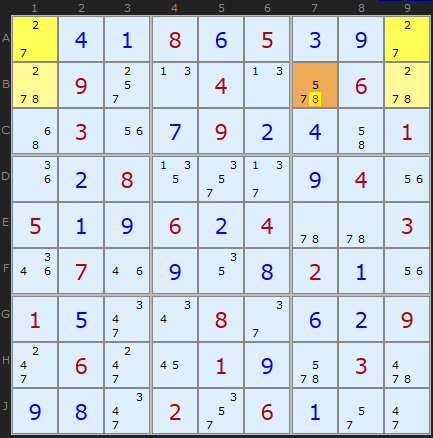
In this puzzle, we have the same pattern of 4 squares in 2 boxes, 2 rows and 2 columns. The floor squares are A1 and A9, and the roof squares are B1 and B9. However, in this Unique Rectangle, each of the boxes contains one floor and one roof cell. This is perfectly fine, but it means that the only unit (row/column/box) that contains both of the roof cells is row 2, so that is the only unit that you can attempt to reduce; in this case, B7 cannot contain a 8. This is called at "Type-2B Unique Rectangle".
You will need to untick 3D-Medusa to see this example.
Type 2C Unique Rectangles
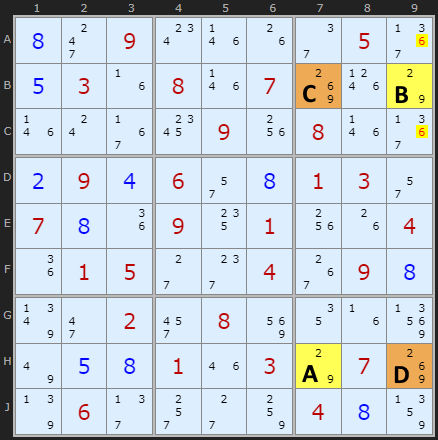
This variation again has the extra candidate but in cells diagonally opposite. You can see the extra 6 in cells B7 and H9 (marked as C and D). 6 Must exist in one of those two cells so any 6 not in the deadly rectangle pattern that can 'see' C and D can be removed.
Not shown in the example is the chance that A or B can also contain the extra candidate 6. Lets say B did - the eliminations hold since those cells can see B9. But if the third extra candidate was in H7 then we could not look in box 3.
Type 2D Unique Rectangles
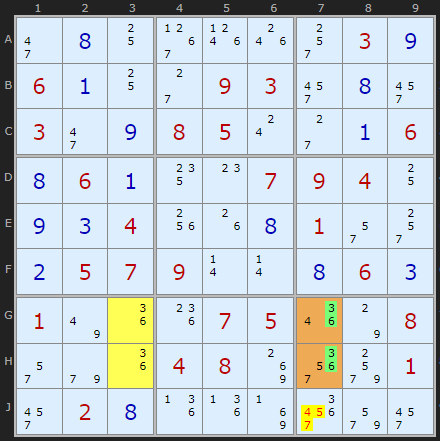
We have a potential Deadly Rectangle on GH37 but if you look carefully 3 and 6 are only found in one cell outside the DR in box 9 (and in column 7). To avoid the Deadly Rectangle we must use candidates outside of it but 3 and 6 only occur in J7. That fact allows us to remove all other candidates from J7.
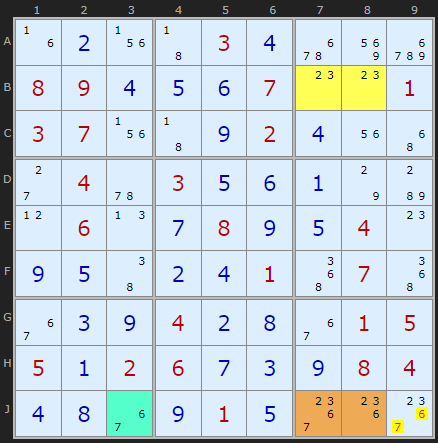
I include this example to illustrate the overlap with Type 3b. I coloured the cyan cell J3 to show where the locked cell is when combined with the roof cells J78 but all this is unnecessary. 2 and 3 only exist in J9 outside the roof tiles so we can go straight to the elimination of 6 and 7 there.
Type 3 Unique Rectangles
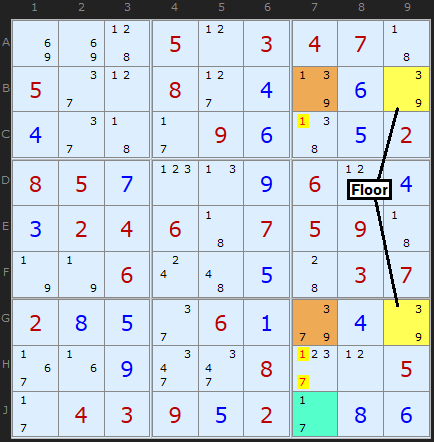
In this variant we have a floor with a pair as before but the roof contains two different candidates (occurring once or twice in each cell of the roof). In the Figure 7 the floor and roof contain [3/9] and the extra candidates in the roof are 1 and 7. Removing both the 1 and 7 from the roof would leave the deadly pattern so either the 1 in B7 must be a solution or the 7 in G7 is a solution. Knowing this does not get us as far as an elimination, however, but we can say that the 1 in B7 and the 7 in G7 act as a pseudo-cell in their own right. The clever bit is using this pseudo-cell with a bi-value cell containing the same candidates. Such a cell is circled on the board – J7. We effectively have a “locked set” like a Naked Pair. 1 will occur in B7 or J7 or 7 will occur in G7 or J7, we just don’t know which way round.
Such reasoning allows us to remove other 1s and 7s on the unit shared by the roof cells (but not the cell we’re using to create a locked set with). There are 1s and 7s in C7 and H7 which can be eliminated.
Type 3b Unique Rectangles
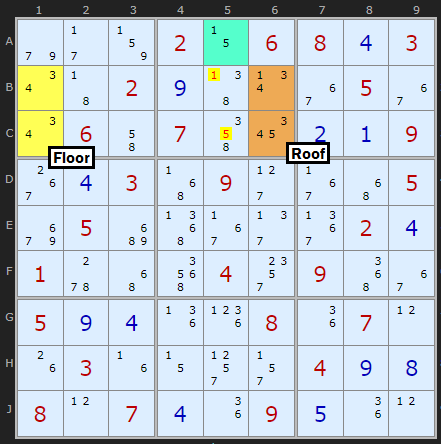
There is a compliment to Type 3, where the roof cells share the same box and that means the floor must be in a different box. Cells B1 and B2 form a pair with 3 and 4. These can see two cells in column 6 which also contain 3/4 as well as a 1 and an 5. We need to match this 1 and 5 in the roof cells with a bi-value cell to make a locked set (effectively a Hidden Pair). This can be along the row or column the roof cells are align with or in the same box. The cell we want is A5. No other 1s and 5s can exist in the same box so we remove 1 from B5 and 5 from C5.
I'd like to credit Hervé Gérard for the first example which he sent to me in November 2013 and later Tom Morrin for stating the box should be used as well.
Type 3/3b with Triple Pseudo-Cells
So far Type 3 and 3b have worked with a pseudo-cell linking with a bi-value cell to make a pseudo pair. This is a valid locked set. Well, locked sets don't have to be pairs, they can involve three candidates over three cells.
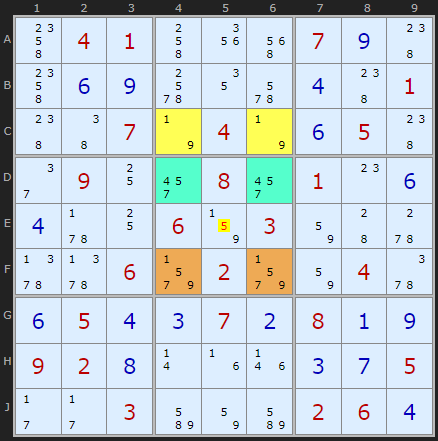
All credit to David Hollenberg for working this insight that nicely expands the strategy.
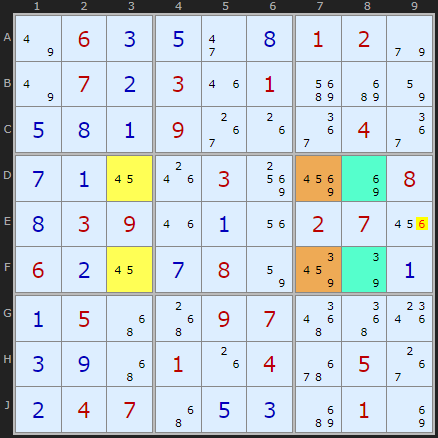
Here is a triple with a slightly different pattern, also from David Hollenberg.
There are three candidates {3, 6, 7} in the pseudo-cell (the extra candidates in the roof). Instead of looking for an extra candidate to make up the triple in two other cells we look for all three candidates {3, 6, 7} in those two cells. These are in D8 and F8. These form a triple with the pseudo-cell in DF7. Naked Triple rules apply so we can eliminate the 6 in E9.
Uniqueness Type 3b (Col) at DF37
- removing 6 at E9 (triple with D8+F8)
Type 4 Unique Rectangles
- Cracking the Rectangle with Conjugate Pairs. (See also Extended UR Type 4.)
An interesting observation is that it is sometimes possible to remove one of the original pair of possibilities from the roof squares. Consider the following puzzle in Figure 10 which is a continuation of the Sudoku puzzle used in the first example.
Look closely at the roof squares, A4 and A6, but this time, don't look at their extra possibilities; look at the possibilities they share with the floor squares.
An interesting observation is that it is sometimes possible to remove one of the original pair of possibilities from the roof squares. Consider the following puzzle in Figure 10 which is a continuation of the Sudoku puzzle used in the first example.
Look closely at the roof squares, A4 and A6, but this time, don't look at their extra possibilities; look at the possibilities they share with the floor squares.
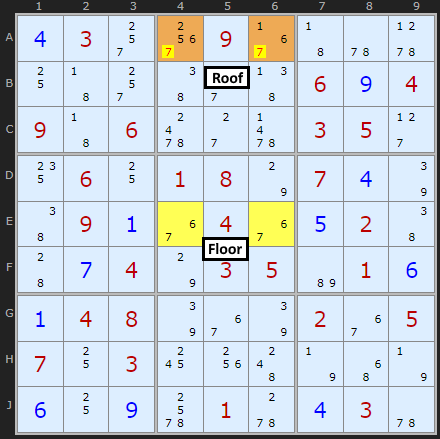
If you look carefully, you'll see that in box 2, the roof squares are the only squares that can contain a 6. This means that, no matter what, one of those squares must be 6 - and from this you can conclude that neither of the squares can contain a 7, since this would create the "deadly pattern"! So you can remove 7 from A4 and A6.
Nomenclature: When two squares are the only two squares in a unit that can have a particular value, they are referred to as a conjugate pair on that value.
This is an example of a "Type-4 Unique Rectangle". As you have probably realised, since the roof squares are in the same box, you can search for conjugate pairs in both of their common units (the row and the box, in this case).
Type 4B Unique Rectangles
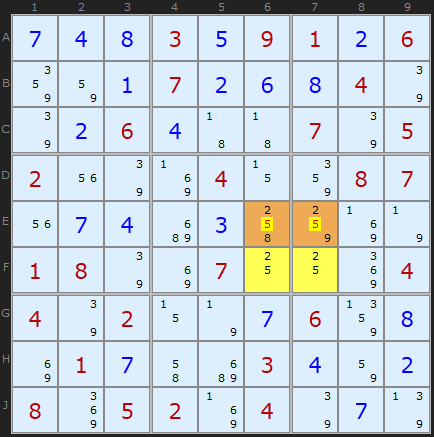
In this case, since 2 can only appear in row E in the roof squares, 5 can be removed from both of them.
As Type-4 Unique Rectangle solutions "destroy" the Unique Rectangle, it is usually best to look for them only after you've done any other possible Unique Rectangle reductions.
Type 5 Unique Rectangles
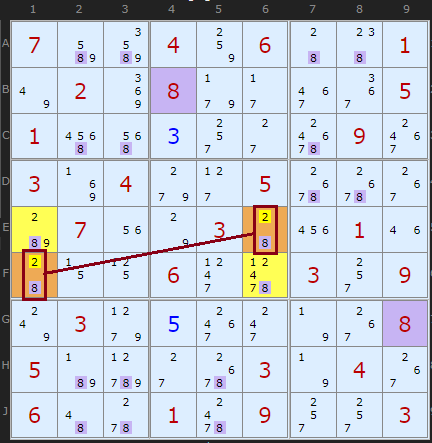
As of January 2021 we have a new Unique Rectangle elimination! Thanks to Ivar Agy from Norway who shared an example with me. Not to say that it might have been discovered elsewhere, I can't check, but please come forward if there are earlier references. Since it is vaguely related to Type 1 (in that it attacks candidates in the rectangle, not outside), and is quite simple to spot, the solver searches for it after Type 1 and before the others. However, I am obliged to call Type 5 since I don't want to re-number everything.
Any rectangle across two boxes that contains two candidates in all four cells might have two opposite corners containing only two candidates, like the {2,8} in E6 and F1. If one of those candidates is linked to the other corners with strong links (ie no other 2s or 8s in the two rows and two columns of the rectangle), it could create a Deadly Rectangle. We are looking for a diagonal Naked Pair - each cell can't see the other, but it is locked. If 2 (the weakly linked candidate in the pair) was ON in either E6 or F1 it would force 8 to be in the other corners. This is not allowed so 2 can be removed from the Naked Pair. Very cool.
Ivar's example can be found if you turn off 3D Medusa first.
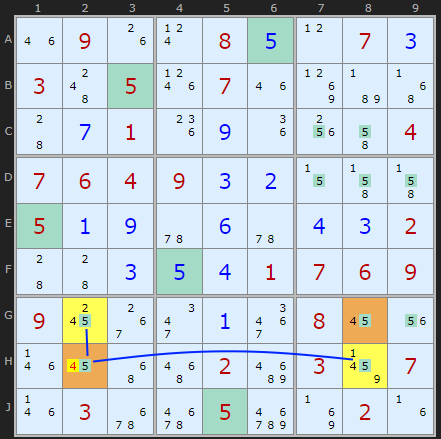
(untick XY-Chains) : Load Example or : From the Start
Up to 2024 I was detecting a pattern where all four candidates (8 in the example above) had strong links forming a loop all the way round. This was too restrictive. If just one pair of strong links exists we can eliminate on one end. In this example there are strong links from H2 to G2 and from H2 to H8. So if H2 is 4 then both G2 and H8 are 5, causing G8 to be 4. But this is a deadly pattern, so H2 cannot be 4.
Uniqueness Type 5: removing 4 from H2 because if true it would create a Deadly Rectangle with G2 and H2
Unique Rectangle Exemplars
These puzzles require two Unique Rectangle strategies at some point but are otherwise trivial and only requires singles.They make good practice puzzles.
Created by Klaus Brenner

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Howard Weiss
I have implemented the logic in the section on Uniquerectangles, but I am finding that there are many more possible DeadlyPatterns in the examples for UniqueRectangle that are not found per this section
I took a different approach. For each cell which contained one of the values in the floor cells, I set that cell that value and then "solved" using Naked Pairs, triples etc. This turned up a number of additional deadly pairs
For instance, in the first example, setting cells H1 or H2 to 9 create deadly patterns with cells A1 and A2
In the second example, setting F5 to 4 create a deadly pattern with E5, E8 and F8 (but, interestingly setting E5 to 4 does not create a deadly pattern)
Do you agree?
... by: Howard Weiss
Rectangle wtih floor A1 and A2 and roof H1 and H2 is also a Type 4 rectangle (eliminate 9's)
... by: Wolfgang M.
when I was studying your explanation of UR Type5, I struggled over the enclosed sentence :
(ie no other n in the two rows and two columns of the rectangle)
where I could not imagine what you meant by the placeholder "n"
in this sentence.
Could this please be explainded more specific - thank you.
Thanks to Autoclear I'm now able to solve all 4/5 levels each Day.
Regards Wolfgang
It refers to the possibility that the corner candidates (in this example 2 and 8) might be strong links and I was reminding the reader what a strong link was (probably unnecessary at this advanced level)
Glad to see you solving high grade puzzles
... by: Cerberus
... by: Alan
"As you have probably realised, since the roof squares are in the same box, you can search for conjugate pairs in both of their common units (the row and the box, in this case)"
I assume that the conjugate pair in figure 10 are the 6s in the roof squares, which have to be in the same row or we wouldn't have a unique rectangle, so how can the box come into it? I'm probably misunderstanding something.
... by: martin
1. A deadly patter remains 'alive' even if some of the corners of the UR have been resolved.
Up to three corners can be resolved. Once the fourth corner is resolved, obviously
the result is either deadly or avoided. With three resolved corners, the fourth corner
therefore (to avoid) needs to discard the candidate found in the diagonally opposite cell.
2. Since many interactive solvers do not distinguish in their display between resolved and
preset cells: That distinction is vital!! A preset cell by definition can never be part of a
deadly UR!! In fact, that is what presets are all about: avoiding these deadly patterns.
Think of the empty board as a humongous deadly pattern!
Similarly, when posting examples, the distinction could be very important.
If you’ve not see it, Avoidable Rectangles use this information
... by: martin
when there is the same pair present at different positions.
Applying Hodoku type 6 multiple times resolves the Types 4, 4B and 5 here.
The same is true for Type 1, with the caveat of the extra condition checks, which are,
however, trivially fulfilled.
... by: Aleksandra Z
If a rectangle across two boxes has opposing corners with only the same two candidates X/Y, and if one candidate X has just one strong link to an adjacent corner, then X can be removed from the other corner. The reason is that placing X there would force adjacent double Y, but then the strong link demands opposite X, which is the ambiguous pattern we are trying to avoid.
This is an example puzzle, which reaches that scenario if XY-Chain and 3D Medusa are disabled:
000000025002753004900800000280010050030408010010020078000009007300586200690000000
It occurs in the rectangle AC37, and it becomes available immediately after A7 becomes 3/7 along with its opposite C3, also immediately before the solver finds other unique rectangles. From here, it suffices to note that 7 is strong in row C—that alone is enough to remove 7 from A3. Independently of that, because the other candidate 3 is strong in row A it can be eliminated from C7.
As it happens, 7 was also strong in column 7 (and 3 strong in column 3), but I emphasise that only one of those strong links are required for an elimination. The reduced need for strong links makes this partial pattern much more common; unlike the full Type 5 pattern (or the very useful Hidden Unique Rectangle pattern!), neither candidate is required to form an X-Wing.
Personally I imagine it as a "partial unique rectangle" or perhaps a "unique rectangle edge elimination" given that demanding uniqueness risks eliminating a candidate from one edge, but in the context here it is described very well as a lighter version of Type 5!
... by: Mika
... by: David Harkness
In this example, the UR is in BC69. Since 347 form a hidden triple in C4, C5, and C69 (the pseudo cell), 5 and 6 may be eliminated from C4 and C5. It does not allow eliminating 56 from the floor cells, however.
Load Sudoku
Unfortunately, the naked pair 56 in C1 and C3 eliminates the 6 from C6 and C9, breaking the UR.
... by: David Harkness
It seems type 3b should extend to naked quads and hidden pairs/triples/quads as well.
Cheers,
David
... by: Robert
a) B2 and B3 are in the same cage, and D2 and D3 are in the same cage, or
b) B2 and D2 are in the same cage, and B3 and D3 are in the same cage.
We could also have all four in the same cage, but this is precluded if we are using the "killer cage convention".
... by: Robert
So this idea that all regular Sudoku strategies also work on Killer Sudokus - I don't think it extends to "uniqueness" strategies, at least not without some additional assumptions on the cages.
This can be seen in Killer #5768 (June 22). Use the solver until it decides to remove "5" from cell J7. This is based on a "UR" strategy, and ultimately finds one solution. However, this is another solution that does have a "5" in J7 - the inference, that the 5 can be removed, is only valid in one of the two solutions.
... by: Steve Benoit
I think I've seen your type 5 Unique Rectangles before. It took me a while to remember where... Check out Sudoku Swami's "Unique Rectangles Part 2 / Sudoku Tutorial #21" on Youtube beginning at time-stamp 12:32. He refers to them as UR-Type 6.
Fantastic website by the way! I wish I had found it much sooner...
Steve
... by: Tapio Ranta-aho
I wonder if this can be a version of unique rectangles? This happened once and candidate 5 appeared to be correct, but I don't know that wasn't just a coincidence.
___ ___ ___ ___ ___ ___ ___ ___ ___
___ ___ ___ ___ ___ ___ ___ ___ ___
___ 12_ 12_ ___ ___ ___ ___ ___ ___
___ 12_ ___ ___ ___ 12_ ___ ___ ___
___ ___ ___ ___ ___ ___ ___ ___ ___
___ ___ 12_ ___ ___ 125 ___ ___ ___
Thanks,
Tapsa
Assuming the "12" pairs are Naked Pairs (no other candidates), this is virtually a "stretched" Type 1 UR.
Also @Andrew
I refer you to Jonathan Handojo's comment on 2021-06-9 finding that the Solver skips UR's and jumps to WXYZ, similar to my earlier comment on 2019-12-16.
I also found a sorta Type 5 in your daily puzzle for 2023-01-21 but not in the Solver order, which I will try to retrieve and send separately.
As always thanks for a fabulous website!
Ciao, Pieter
... by: Maggie Mc
... by: Anonymous
Seeing the website hasn't been updated for about 8-9 years, this type has been known for a long time already.
... by: Anonymous
... by: Pieter, Newtown, Oz
Re Type 5 URs
1. The output from the solver says, for example, "Uniqueness Type 5: removing 2 from E6 and F1 because if true it would create a Deadly Rectangle with E1 and F1". It should read "... would create a Deadly Rectangle with E1 and ***F6***".
2. I've noticed odd characters in some places in the text, such as "Thanks to Ivar Ag�y from Norway" in Type 5 above. Also in the Digit Forcing Chains strategy - Second Example "DIGIT FORCING CHAIN: because … -5[G9]+5[F9]-5[F1]+5[C1] ��-4[C1]+4[B1".
I find it curious that you "updated" version 2.08, twice, rather than naming them 2.09, 2.10?
Thanks as always
Ciao
Pieter
... by: alpreucil
Never been down except for server migrations
... by: Tunner
... by: SG
Click on this link
... by: BobW
I believe the new type 5 that you posted (January 2021), has been known for some time.
It is described on the enjoysudoku forum, along with many other variations of UR's having two extra candidate cells, located diagonally. That post is dated April 2006. I ran across it while implementing UR's in my own solver last year.
http://forum.enjoysudoku.com/post26448.html#p26448
If I'm not mistaken, the one that you refer to as Type 5 is referred to as UR+2D/1SL (not to be confused with UR+2D or UR+2d).
I spent many hours going through that post and many others in the same thread. The logic for many of them is so convoluted that it made my head spin. It occurred to me that it would be much simpler just to work out the truth tables for them. One day, having nothing better to do, that's exactly what I did. I worked out the truth tables for every possible combination of UR's with 2, 3 or 4 extra candidate cells ("Guardian cells" in my notation) with every possible combination of strong links between the various cells. Summarizing only patterns that give eliminations of internal UR candidates, I found 8 different UR+2 patterns with adjacent guardians, 11 different UR+2 patterns with diagonal guardians, 18 different UR+3 patterns, and 5 different UR+4 patterns.
When I refer to the number of patterns found, I've excluded reflections and rotations of the basic patterns. I implemented the resulting rules using a lookup table in my solver.
There's not enough room here to give all of my results, but if you contact me by email, I'd be happy to share what I've done.
That sounds like thorough work, well done. I should take it all in and completely redo the UR. Big job though.
... by: Jonathan Handojo
If you use the Solve Path with every checkbox ticked, you get a WXYZ-Wing evaluation. It seems to have skipped through the Unique Rectangles strategy when there's one in B7, B9, J7 and J9 that allows the eliminations: 8 from J7, 6 from J9, and 8 from B9. Either value you force into them forms the deadly pattern, so I solved the puzzle quite with ease after using this. Now I'm not too sure of the rules with this, but I only saw it through forcing.
... by: Pieter, Newtown, Oz
As always thanks for a fabulous website!
Solving your Daily Sudoku for 2019-11-15 I believe it has a Type 4 UR which the solver does not find.
After solving the basics we are left with this board and the solver next finds an XYZ-Wing.
If you backstep and turn XYZ and X-Cycles off, I would expect the solver to find what I believe to be a Type 4 UR in EJ89, with the floor in E8/9, and the conjugate pair of 4's in J8/9, eliminating the 5's in J8/9. However, the solver skips all URs and finds a WXYZ.
Is this correct/a bug?
Ciao, Pieter
... by: Niki
I ask because I just spotted one for the first time in an extreme jigsaw puzzle - it was a 3/3b (triple), and it made the rest of the puzzle collapse nicely. Despite the jigsaw shape, it still fell in two rows, two columns, and two boxes just like it ought. But I was hesitant to follow up on it, having never seen the Unique Rectangle strategy mentioned in conjunction with jigsaws.
... by: Pieter, Newtown, Oz
I am confused by the solvers handling of URs in this partially solved puzzle
I have spotted what I believe to be a clear Type 4 UR in CH45, on 1/9. However, the solver finds a Type 3b combining with the 5/8 in H6 and then the puzzle solves.
I tried unchecking URs and the solver finds a Hidden UR Type 1 and eliminates the 1 in H5. Why does it not eliminate the 1 in H4? Taking Steps to try again, even re-checking the UR box, the solver moves to a HUR in EF28.
A 1 in H4 would create the Deadly Pattern. Why isn't it eliminated? Bug?
Ciao, Pieter
... by: digituer
The pseudo-cell concept in Type 3 is great! I think based on this pseudo-cell concept, a hidden pair strategy can also be applied.
12 . . | . . 12AC
. . . | . . .
12 . . | . . 12AB
---------------------------
. . . | . . 12FE
If the 2 roof cells and that extra cell are the only three cells holding 12 in the unit, then FE can be removed (ABCFE can be any numbers).
... by: AAHoffman
A1=A2={2,4}
D1=D2={2,5}
G1=G2={4,5}
as a simple example. Solutions devolving to this can be eliminated.
Multiple floors can be bent and don't have to be in a straight line, i.e.,
A1=A2={2,4} (row)
D1=E2={2,4} (note: forms a diagonal that "bends" the structure)
D4=E4={2,4} (column)
Another possibility uses naked triples in three rows, i.e.,
{A1,A2,A3}={2,3,4} (in any combination (except naked single or pair), i.e., {23},{24},{34})
{D1,D2,D3}={2,3,4} (i.e., {24},{34},{23})
{G1,G2,G3}={2,3,4} (i.e., {34},{23},{24}).
All these patterns occur often enough to be useful.
By the way, not sure how nomenclatures are standardized but I have named these "meta" strategies instead of naked rectangles... because they are a rule dependent on a rule of the game. When three digits are involved as above, I call them "triple meta".
... by: Barry
... by: Thinkist
I came to a clearer realization on why I dislike uniqueness strategies: they mess with the solution count if a sudoku happens to have multiple solutions, erroneously decimating otherwise valid solutions. I point you to an example of mine here. It has 63 solutions, but 4 URs erroneously deduce it to 3, and then one use of the BUG strategy erroneously deduces it to 1. So, this makes the puzzle appear valid when in fact it should have 63 solutions all along and the solver should fail to complete correctly. The chaining, netting, and simple combinatoric strategies don't mess with the solution count. In those cases, simply because there is more than one solution, the solver will merely fail to complete correctly rather than throw up an error. I believe that any puzzle (or "puzzle", if you will) that throws up a contradiction should have 0 solutions from the start, not because of a uniqueness strategy.
Re-reading your reply to my first comment, I'm glad that you've not decided to add a solution count before any logical solving takes place, as that would of course ruin the purpose of using the solver, which is to showcase a bottom-up approach to sudoku solving rather than cheat it with a brute-force top-down approach.
And for the record, I realize that any valid sudoku puzzle should have only a single solution. The point I'm trying to make is that uniqueness strategies aren't the best way to find it (which is why I still have them unchecked in the solver). In essence, they assume what you are trying to prove (via chaining, netting, and simple combinatoric strategies): that the puzzle has a unique solution.
The problem with a) is that I don’t know of a solver that claims to solve all puzzles (certainly I don't pretend mine is the most advanced and I have a long job queue of improvements) and the problem with b) is that I'm sure a non-valid puzzle could accidentally complete giving the impression of a single solution solved logically. Wish I had one to hand, but I strongly suppose it.
However there is a good practical reason for using logic rather than brute force for solution counting, as the attached graph tries to show. It’s a crude diagram I knocked up to illustrate a point in a previous correspondence, but there is a point at which brute force becomes much slower than logic and it’s a function of clue density.
... by: Master Shuriken
If you have, for example empty boxes in A1, A2, H1, J2, H9, J9 with 2 clues (1,2) in each box, this wouldn't be possible.
You could extend this *uniqueness chain* as long as you like through the puzzle and extend it to triples, too, (as long as you make sure that there would be 2 solutions if everything else was filled in).
Like the unique rectangle, it would tell you something which is not possible, and could help eliminate clues, etc.
... by: dshaps
Quote
If you look carefully, you'll see that in box 7, the roof squares are the only squares that can contain a 7. This means that, no matter what, one of those squares must be 7 - and from this you can conclude that neither of the squares can contain a 9, since this would create the "deadly pattern"! So you can remove 9 from H1and H2.
Unquote
How is it that deadly pattern will get created, if either of roof squares contains 9. Can you please elaborate?
... by: PCForrest
"In the 'Type 1 Unique Rectangles' example (Unique Rectangle Figure 2), can't the same explanation be used for the 2 and the 9 in D2? Logically, it doesn't make sense to eliminate the 2 and the 9 in D1, but not in D2. It seems that by eliminating the 2 and the 9 in D1, we move the deadly rectangle corner over to D2. Should we then use the same logic to eliminate the 2 and the 9 from D2? Or are we ignoring that square for the sake of the example?"
D2 does not a rectangle make, let alone a unique rectangle. To be valid, all four cells must occupy exactly 2 rows, 2 columns and 2 boxes. Logically, it makes perfect sense to eliminate both 2 and 9 from D1 but not from D2, for the simple reason D2 must take the value 2 in the final solution. If you eliminate the 2, you immediately invalidate the puzzle. The logic that applies to D1 does not apply to D2. We are ignoring D2 for the simple reason it plays no part in this unique rectangle.
... by: Sherman
For example, figure 7 in the Type3b UR discussion has strong links between all four 6's in the UR. If 7 is placed in cell E6, 6's must be placed in cells E4 and J6, forcing a 7 in J4 - a deadly pattern. So 7 cannot go in E6. Likewise, 7 cannot go in E4.
The HUR logic can also be applied to figure 6, removing a couple of 3's.
Type 4/4b can be analyzed with HUR, which results in the same eliminations as UR. So in some sense Type 4/4b is really part of the HUR logic.
When you find a Type 2/2b or 3/3b UR, it pays to look at the strong links in it to see if HUR can also be applied. Apply HUR after UR, as it destroys the deadly pattern.
... by: Dan, UK
how about this:
http://www.sudokuwiki.org/sudoku.htm?bd=000764381364010572187235000013082607000601035000090018200000159001020700070150820
my solver says:
Unique rectangle type 3 at r2c4, r2c6, r8c4 and r8c6 allows 4 and 6 to be eliminated from r8c1, r8c2
you can see a screenshots from my solver here:
http://danhen.xf.cz/pics/shared/su_ur3_01.jpg
http://danhen.xf.cz/pics/shared/su_ur3_02.jpg
explanation: floor if clearly defined. As the roof contains additional candidates defined as 346, we can search for TWO cells, which contains some of these candidates, but only them, as defined in naked triple rule. As we found two cells 46 and 346, we can consider this as triple (two found cells and two cells from the roof of unique rectangle) and eliminate candidates 346 from the other cells in the unit (as seen on screenshots).
HODOKU solver can recognize this 'triple-extended-type 3' as well :)
http://hodoku.sourceforge.net/en/show_example.php?file=u301&tech=Unique+Rectangle+Type+3
The same logic can be used for searching for 'quad', that means four additional candidates in the roof of rectangle, and we'll be looking for THREE cells in a unit, which contains some of those candidates, defined by the rule of naked quad. My solver should be able to solve such a problem, but unfortunatelly I didn't find any game to match this problem :( If ANYONE is able to share game with such a kind of unique rectangle, feel free to post it :)
Dan
... by: Random Sudoku Enthusiast
Logically, it doesn't make sense to eliminate the 2 and the 9 in D1, but not in D2.
It seems that by eliminating the 2 and the 9 in D1, we move the deadly rectangle corner over to D2. Should we then use the same logic to eliminate the 2 and the 9 from D2?
Or are we ignoring that square for the sake of the example?
... by: jaswant singh =sriganganagar INDIA
... by: DanielKlaus
there are 7 eliminations.
... by: JesseChisholm
Picture the group "B" in figure one (where "A" is the Deadly Pattern)
Add an expanded copy of group "B" such that:
* there are four boxes with a pair of 7/9 cells
* there are four rows with a pair of 7/9 cells
* there are four cols with a pair of 7/9 cells
These eight 7/9 cells together form a Nested Deadly Squares pattern.
-Jesse
... by: gerp124
I can accept that they're part of the game, and may be the only way to solve a board sometimes, but it seems like such an arbitrary rule. What's so special about singularity? Yes, that was intended as a joke, but I've never seen any aesthetic offense in a puzzle with more than one solution. Except that a single solution cannot then be published. But I've already made my case regarding published solutions :-)
... by: gerp124
And thanks very much for such a wonderful website- for years, until I discovered this website, I was completely befuddled as to the solutions that are always published- they are not needed, and they are not helpful. If you can finish, you don't need the solution, and if you _can't_ finish, you don't need the solution, rather, you need to know _how_ to get the solution. And this website has provided an wonderful practical education in reasoning via sudoku!
... by: gerp124
In the Sudoku of the Variety section of Minneapolis Star Tribune for Sunday has these values _given_:
2D=9
2E=7
7D=7
7E=9
Does it make a difference, that the values were _given_, as opposed to being values that needed _solving_? The entire puzzle constitutes the _solution_, doesn't it? And these values could move, yielding a second solution, true?
Here is the board as published, and thanks for in any thoughts.
http://www.sudokuwiki.org/sudoku.htm?bd=800002000004000009060908003090004700075801930006300010500403090900000200000700008
... by: Sonalita
A fundamental premise of Andrew's excellent solver (and any algorithm based solver) is that the puzzle MUST have a unique solution.
It is generally accepted that the definition of a valid sudoku puzzle includes the constraint that there must be a single solution, so your statement of "not believing in uniqueness strategies" makes no sense.
... by: Thinkist
I am thinking of adding a solution count to the start of the solve "take step" and stop any further progress until the puzzle is fixed. Mostly it is data entry and it causes confusion is people don’t check the solution count first.
... by: B.N.Hobson
... by: Anton Delprado
If we look at type 2 cells from this concept then the virtual cell has a single value and is "solved". This can then be used to eliminate that value in any cell that can see both cells. So type 2 are kinds of type 3 in a sense.
This can also be extended to naked multiples in the joined row/col. For example if roof cells are in the same row and have three non-deadly values that are shared in two other cells in the row then those values can be removed in other cells in the row.
Yes, I have a feeling it might be possible to generalize and extend UR types. I'm in touch with someone else who has a good idea about re-organizing the families under different rules. I think you are on a similar track
... by: Chuck Bruno - Virginia
... by: Alan Freberg
Here's one that I had on hand when I wrote my previous post, but had yet to logic it out. It's fairly straight forward, though. It appears to be a Type 5b as there are three candidates in the ceiling instead of two as in Type 3 or my previous examples.
In the Daily Nightmare for Dec. 29, 2005 the floor cells contain 3/4 in 2 B/D. The ceiling is in Col. 1 where the unsolved cells contain: 6/7/9 (A1), 3/4/7/9 (B1), 3/4/6/7 (D1), 4/7 (E1) and 6/7/9 (H1). The ceiling in cells B/D1 contain the Strong Links (if we can still call them that) 6/7/9. As you explain two cell tri-values on pg. 124, A1 and H1 will be reduced to a Naked Pair whichever of the three is the true value in the ceiling cells . Delete 7(E1).
Thanks again,
Alan Freberg
... by: Alan Freberg
A few months ago I purchased "The Book" with the intention of first reading it and then trying to solve all of Ruud's Daily Sudoku Nightmares. "The Book" was an excellent read. It illuminated several dark corners. There are still some dark corners left, but they are my failings and not yours.
One thing I'm always trying to do with a Sudoku is to find something new or somehow push the envelope past what I know. Having read your book lead me to something of that nature while working on the Nightmares.
My solutions for the Daily Nightmares for March 30, 2006, Feb. 15, 2006, Feb. 2, 2006, Dec, 19 2005 and Dec. 16, 2005 contain a pattern that I have not seen before. They are based on a combined application of Unique Rectangles and Aligned Pair Exclusion. At first I thought they were a variant of your Type 3 URs, but, since they allow for more deletions than Type 3 would, it appears that they are a new variation. I call them UR Type 5 or UR APE App(lication).
In the March 30 DN (please pardon my reverse chronological order, but if you choose to look them up it is the order in which you will find them.) the floor pair are 4/5 in Col. 5 A/C. The ceiling is in Col. 2 where the unsolved cells contain the following candidates: 4/5/6/(A2), 6/8 (B2), 4/5/9 (C2), 4/5/8/9 (E2) and 8/9 (J2). 6/9 are the Strong Link pair in the ceiling. According to the Type 3 rule there are no deletions possible. However, on pg. 122 of the chapter on APE the following rule is given--"Any two cells with only abc exclude combinations ab, ac and bc..." Applying this rule to this formation we find that the two cells B2 and J2 contain 6/8/9. However one looks at it, the values for the extra candidates in the ceiling cells are accounted for and 8/9 can be deleted from E2. Notice that 8(E2) is not one of the Strong Link candidates.
In the Feb. 15 DN the floor pair are 3/7 in Row E 1/2. The ceiling is in Row B. The unsolved cells in B contain: 1/3/7 (B1), 3/7/8 (B2), 8/9 (B4), 1/9 (B5) and 3/9 (B9). 1/8 are the Strong Link candidates in the ceiling and 1/8/9 in B4/5 fulfill the APE rule requirements. Delete 9 (B9).
In the Feb. 2 DN the floor pair are 7/8 in Col. 2 G/J. The ceiling is in Col. 6. The unsolved cells in Col. 6 contain: 3/6 (C6), 4/6/8 (D6), 4/6 (E6), 4/7/8 (G6) and 3/4/7/8 (H6). 3/4 are the strong links in the ceiling. 3/4/6 in C/E fulfill the APE rule requirements. Delete 4/6 (D6).
In the Dec. 19 DN the floor pair are 2/6 in Row H 2/3. The ceiling is in Row B. The unsolved cells in Box 1 are: 5/7 (A1), 1/5/7 (A3) and 6/7 (C2). 1/5 are the Strong Link pair in the ceiling with 1/5/7 in A 1/3 completing the APE requirements. Delete 7 (C2).
In the Dec. 16 DN the floor pair are 4/6 in Row D 1/2. The ceiling is in Row G. The unsolved cells in Row G contain: 4/6/7 (G3), 3/5/7 (G7) and 3/5 (G8). 5/7 are the Strong Link pair in the ceiling with 3/5/7 (G7/8) fulfilling the APE rule requirements. Delete 7 (G3).
If this is indeed a new application then you are the godfather of this baby as your explanation of the APE rule pointed the way for me.
Thank you very much,
Alan Freberg
... by: JCS
I am new to this site but I end to agree with Andi. There is no deadly pattern if R5C6 contains candidates 356.
Applying simple colouring technique to the puzzle will show that 2s can be removed from R2C8 R7C2 R8C7 and R8C9. That causes R2C8 to be a 9, R7C8 a 2, R7C3 a 9, R1C1 a 9, R1C5 a 4, R4C5 a 9, R4C6 a 7. At this stage that leaves 356 as candidates for R5C6. The puzzle can then easily be solved without applying that "unique rectangle" technique ending with a 6 in R5C6.
... by: csvidyasagar
1. You are absolutely correct. Type 4 and Type 4 B rely one logic that roof cell may contain a digit which is confined to that row or column or block and can not be removed. So the other digit can be easily removed from thase two cells in Roof Row. In Type 4 example, the Roof Row C has 1,5,6 in cell C1 and C3. Either digit 1 or 5 can be removed to ensure Deadly Pattern does not result leading to two solutions. But 5 is confined both in Row C and in Block Top Left or Block 1. So digit 1 can be removed from both cells in Roof Row C.
Have I confused you further ?
with regards,
CS Vidyasagar
... by: csvidyasagar
1. When you have three out of four corners in a unique rectangle have two digits (in this case 5,7), then the fourth corner can not have 5,7 as this will have all four corners having 5,7.This is a Deadly pattern as you can have two different solutions. But for a pure Sudoku you have to have only one or unique solution. That is possible only if you remove digits 5,7 which other three corner cells of Unique Rectangle have.
2. You aim must be to reduce maximum number of digits from cells containing multiple candidates. When you can remove 5,7 from 3,5,6,7, of cell R5 C6, you are reducing time to solve the puzzle but also reducing complexity. More candidates in ells mean more complexity and require more time to solve.
3. When you remove 5,7 from cell R5 C6, you see in column 6 you have digit 5 in cell R2C6 and digit 7 in cell R4C6. So the rule of all columns, rows and boxes to contain all digits from 1 to 9 is met.
4. I could only think of three reasons as to why you can remove 5,7 from cell R5 C6.
Have I confused you further ?
with regards,
CS Vidyasagar
... by: csvidyasagar
The four cells you have mentioned have the following pattern:
Col 1 Col 4
Row A 1,5,6 1,5,6
Row D 1, 5 1,5.
This is similar to Unique Rectangle Pattern 2B. That is floor cells are 1,5 and Roof cells are 1,5,6. Since these form a unique rectangle with 1,5 being common in all the four cells to avoid Deadly Pattern ( of all cells having 1,5), you have to keep 6 in Row A i.e. Roof cells. That means 1,5 will be removed later from Roof Cells in Row A.
But you can not have two 6s in Row A (Roof Row) as any row can have only one digit in one cell. So remove 6 from any other cell in Roof Row A or in the Block /Box of Roof cells.
Have I confused you further ?
with regards,
CS Vidyasagar
... by: Harmen Dijkstra
... by: Wiking 48
I'm quite new on this.
why do you bother with such a non-defined sudoku?
There are many more than 17 sulotions! Check for yourself, you see that 24, 42 in the left of your grid can be excanged.
Is there any idea to fight against non-defined?
Upper left corner can also be 1, 2 or 3 which gives a lot of solutions..
Down left corner in your example is 7 in one example which is quite common among the sulotions, 1 is more rare but possible...
... by: Harmen Dijkstra
. 9 . | 5 . . | 6 4 7
6 . 5 | . . 7 | . 9 3
. 7 . | . . . | 2 5 8
-----------------------
. 5 6 | . 7 . | 9 . .
. . 7 |9 . 5| 3 8 6
. . 3 |8 . 2| 4 7 5
-----------------------
. . . | . 5 .| 8 3 9
5 6 . | . . .| 7 2 .
. . . | . . 8| 5 6 4
If you filling this sudoku in the sudoku solver, the solution Count will say that there are 17 solutions. But if you try TAKE STEP then you will get only this sudoku (with Unique Rectangles):
2 9 1 | 5 8 3 | 6 4 7
6 8 5 | 2 4 7 | 1 9 3
3 7 4 | 1 9 6 | 2 5 8
-----------------------
8 5 6 | 3 7 4 | 9 1 2
4 2 7 | 9 1 5 | 3 8 6
9 1 3 | 8 6 2 | 4 7 5
-----------------------
7 4 2 | 6 5 1 | 8 3 9
5 6 8 | 4 3 9 | 7 2 1
1 3 9 | 7 2 8 | 5 6 4
But there are more solutions, for example:
1 9 2 | 5 8 3 | 6 4 7
6 8 5 | 2 4 7 | 1 9 3
3 7 4 | 6 9 1 | 2 5 8
-----------------------
8 5 6 | 3 7 4 | 9 1 2
2 4 7 | 9 1 5 | 3 8 6
9 1 3 | 8 6 2 | 4 7 5
-----------------------
4 2 1 | 7 5 6 | 8 3 9
5 6 8 | 4 3 9 | 7 2 1
7 3 9 | 1 2 8 | 5 6 4
The sudoku solver said that (because of Unique Rectangles) R7C4 has to be a 6, but in this example you see that you get an other solution with a 7.
Is this a fault in the sudoku solver?
... by: CS Vidyasagar
2. One has to understand the logic and solution becomes quite clear. You have seleted many good illustrations which have explained the logic clearly and unambiguosly.
3. Looking forward to more such illustrations.
Kudos for wonderful work you are doing.
with regards,
Vidyasagar
... by: Lea Hayes
Rectangle Cells:
A(1,5,6) B(1,5,6)
C(1,5) D(1,5)
Why remove 1 from both A and B and not either of the following:
A(5,6) B(1,5)
C(1,5) D(1,5)
or
A(1,5) B(5,6)
C(1,5) D(1,5)
... by: Lea Hayes
I do not understand how you came to the conclusion that 1 can be removed? Why not remove 6 instead?
... by: John_Ha
I too was puzzling over that but I think the answer is simple. See Fig 2. (5 and 7) are unsolved in Col 4 otherwise they wouldn't be candidates in R2C4. Similarly (5 and 7) are unsolved in Col 6. Similarly (5 and 7) are unsolved in Row 5. Because the cell at R5C4 is unsolved for 5 and 7, then the centre 3x3 must be unsolved for (5 and 7).
There is therefore no way before now that the cell at R5C6 could have had either 5 or 7 eliminated as candidates because there are no solved (5 or 7) that it can see. The 5 and 7 at R5C6 could not have been eliminated by something happening on R5, nor on C6, nor in its 3x3.
So, the cell at R5C6 MUST have BOTH 5 and 7 as candidates (as well as possibly others, in this case 3 and 6).
Now assume R5C6 is 5 - we get the deadly pattern. So R5C6 cannot be 5. Now assume R5C6 is 7 - we get the deadly pattern. So R5C6 cannot be 7.
So R5C6 cannot be 5 or 7 and both can be eliminated.
... by: Andi
But I do not see why you can eliminate 5 AND 7 for this reason from R5C6. IMHO, if in R5C6 3,5,6 would be possible, well then this would just imply R5C4 and R2C6 being 7 and R2C4 being 5. An "ordinary" solution. OTOH, if in R5C6 3,6,7 would be possible, R5C4 and R2C6 would be 5 and R2C4 would be 7. Quite straightforward, too. My point is: both possibilities would be valid. But I cannot spot a "deadly pattern" here because to remove the ambiguity in this sitatuation, all you can postulate is that *either* 5 *or* 7 must be removed from the possibilities in R5C6. With either number removed, the ambiguity is removed, thus no deadly pattern anymore. But I just don't see why you eliminate *both* 5 and 7 in R5C6?
Am I missing something?
... by: Dennis Daft
Dennis