Guardians
(a.k.a. Broken Wings, Turbot-Fish, Oddagon)
This strategy works with single numbers.
We've already used closed loops of conjugate pairs to find things like X-Wings and Swordfish. X-Wings contains 4 cells in a perfect rectangle. Swordfish requires 6 or 9 cells in a grid. This strategy works with odd numbers of pairs in a loop starting with 5. There are several varieties depending on how 'perfect' the loop is.
Let us use the words perfect pair instead of conjugate pair to mean any number that exists only twice in one unit (row, column or box). This means we can use imperfect to mean a number that occurs three or more times in a unit. (Obviously if it only occurred once it would solve that cell).
Credits: I want to thank Rod Hagglund for explaining this technique although for Type 1 Single Guardians (this first example) Simple Colouring might be simpler logic. Some of the Type 2 and Type 3 Guardians can also be attacked with Multi-Colouring but I've not discovered how with the two examples below.
As of March 2010 this strategy has been deprecated. It is a complicated way of looking at what is ultimately a nice loop with off-chain eliminations. It has been removed from the solver.
As of May 2025 this strategy if being looked at again especially with regards to the more powerful extensions developed in recent years. Diagrams and text have been modernised.
This strategy works with single numbers.
We've already used closed loops of conjugate pairs to find things like X-Wings and Swordfish. X-Wings contains 4 cells in a perfect rectangle. Swordfish requires 6 or 9 cells in a grid. This strategy works with odd numbers of pairs in a loop starting with 5. There are several varieties depending on how 'perfect' the loop is.
Let us use the words perfect pair instead of conjugate pair to mean any number that exists only twice in one unit (row, column or box). This means we can use imperfect to mean a number that occurs three or more times in a unit. (Obviously if it only occurred once it would solve that cell).
Credits: I want to thank Rod Hagglund for explaining this technique although for Type 1 Single Guardians (this first example) Simple Colouring might be simpler logic. Some of the Type 2 and Type 3 Guardians can also be attacked with Multi-Colouring but I've not discovered how with the two examples below.
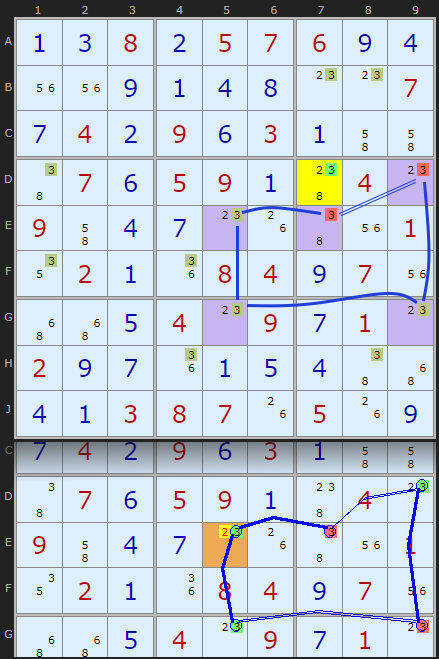
E7 - E5 - along the row
E5 - G5 - along the column
G5 - G9 - along the row
G9 - D9 - along the column
To close the loop we have an imperfect triplet in the sixth box.
The question is: can a closed loop of five candidate cells be constructed with each cell perfectly-paired with the next linking cells in the loop? The answer is no. Such a formation is impossible in a Sudoku puzzle and is called a Deadly Loop. In such a loop, if you "placed" a candidate in any one of the cells and followed the consequences around the loop, you'd generate an automatic contradiction - forcing the number to disappear entirely from a row, cell or block, or to appear twice in a single line or block, depending on how you proceed.
To repeat, In an actual Sudoku there can never be a closed loop of five perfectly paired cells. And that is exactly where the solving technique lies. Any such structure must have one or more cells that disrupt the perfect pairings. We can refer to the cells which prevent one of the pairings from being perfect as guardians. Here's the trick: logically, one or more of the guardians must contain the candidate number. If none of the guardian cells were real, then the pairings would all be perfect and, as was already noted, that is flat-out impossible in a valid Sudoku. Accordingly, we can make the following assertions:
- If there is only one guardian cell, the candidate number can be installed in that cell.
- If there is more than one guardian, any cell that is seen by all the guardian cells cannot contain the candidate number; hence
- If all the guardian cells are in a single column, row or block of the Broken Wing, the candidate can be erased from both the Broken Wing cells in that column, row or block.
Type 1 - Single Guardians
The variants of this strategy depend on how many Imperfect connections there are in the loop. To achieve one guardian there must be four perfect pairs and one Imperfect connection. Figure 1 illustrates this. That one guardian is the cell that disrupts the 5-loop from being perfect. Under Figure 1 is the X-Cycle equivalent chain found by the solver (there are many possible ones).Type 2 - Double Guardians
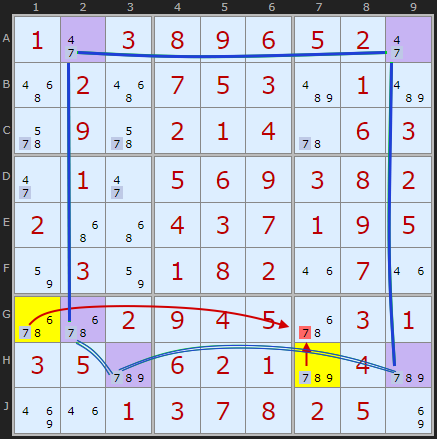
H3 - H9 - along the row
H3 - G2 - within the box
This gives us two guardian 7's in G1 and H7 marked in yellow squares. Whatever cells these two can both 'see' we can eliminate the 7 from them. Since in this example they form the opposite corners of a rectangle we can safely remove the 7 from G7 marked in red. The other corner, H1, contains a solved square.
Solving G7 allows us to complete the puzzle using other strategies.
Type 3 - Disruptive Guardians
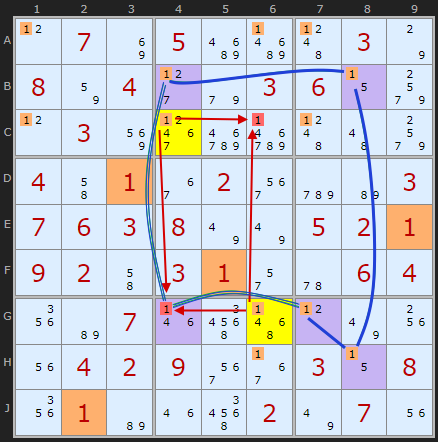
B4 - G4 - along the column
G4 - G7 - along the row
This gives us two guardian 1's in C4 and G6 marked in yellow squares.
Whatever cells these two can both 'see' we can eliminate the 1 from them. Like in the example above, they form the opposite corners of a rectangle but the difference is that we're eliminating a 1 that's actually part of the loop. This is perfectly legitimate and follows from Rule 3 described above. The elimination occurs because G4 can be seen by both guardians.
The Bi-Value Oddagon
I have been reading the forums trying to catch up on the Oddagon discussion. I came across this thread and example by borescoper (2016) and it seemed an accessible pattern. This is not currently in the released server, but I am accumulating useful patterns here.
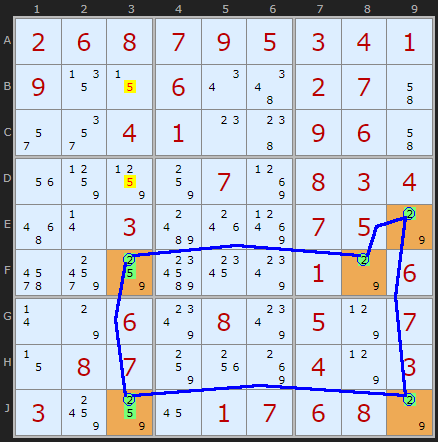
Five bi-value cells in a loop will form a double Oddagon which, without any extra candidates, will be a Deadly Loop since they cannot all resolve to solutions. The double-Oddagon really stands out against the rest of the board as similar paired cells draw the eye.
We need three such pairs plus two more cells with one extra candidate. In bonescoper's example F8, E9 and J9 contain {2,9}. So do F3 and J3 - but they also have 5. This 5 is necessary in that it must be used to avoid the Deadly Loop - so as it aligns on column 3 we can eliminate others 5s in the column.

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Aleksandra Z
Even the actual chain examples are often much longer than they need to be, almost always some shorter part of the chain will suffice, and almost always it could avoid using boxes and stay with rows and columns which form little spirals. I imagine the solving insists first on making a chain as big as it can, even if it would feel a bit more like a human solution with smaller sections which are easier to notice!
The first picture here is quite obvious with the column 7 highlights removed; we have a spiral section which removes 2/3 from Box 6 Row 5 (and indeed Box 5 Row 4, were it needed), placing the 8-digit immediately.
The second picture is similar; retain only the highlights in columns 2 and 9, and we can see a quite large spiral which removes 7 from Box 7 Row 8 and Box 9 Row 7, making a little more progress than is shown. It allows some quite sneaky alternation in the top-right to get a 6 in Box 6.
The third picture is far too complicated, and also a quite good example of chains getting larger than needed! Instead, highlight the 1-positions only in rows 2 and 8 to see a spiral which removes 1 from Box 2 Column 6 and from Box 8 Column 4. That leaves a matching 4/6 pair in the latter rod, which solves a 7 further up in Column 4.
That is not to say that longer chains and box-bridges are never needed, only that just a small spiral piece is sufficient very often!