Solver App for Android and iPhone Strategies for Number Puzzles of all kinds
 
Print Version Get the SudokuWiki Newsletter
 
Solvers
Puzzles
Basic Strategies
Tough Strategies
Diabolical Strategies
Extreme Strategies
Depreciated Strategies
Str8ts
Other
The Logic of Sudoku
Order Str8ts Book 1
Order Now!
Order Str8ts Book 2
Order Now!
  Multivalue X-Wing Strategy
As of March 2010 this strategy has been deprecated. Although useful too look out for in pen and paper solving it is a strict subset of several chaining strategies and therefore has been removed from the solver. The documentation will remain on this site

I've named this strategy Multivalue because we're dealing with several candidate values but the formation is exactly as an X-Wing, infact it also follows the generalised x-wing as described above.
Take a look at this rectangular formation made from the yellow and brown cells. Connecting the two yellow cells is a conjugate pair of 6, the only two sixes in the row. In the other row connecting the two brown cells is a conjugate pair of 5. What connects the cells in the columns are the additional candidates, in this case 1 in column 1 and 9 in column 9. Note that there are additional 1's and 9's in these columns. These are the candidates we can eliminate and they are highighted in green cells.

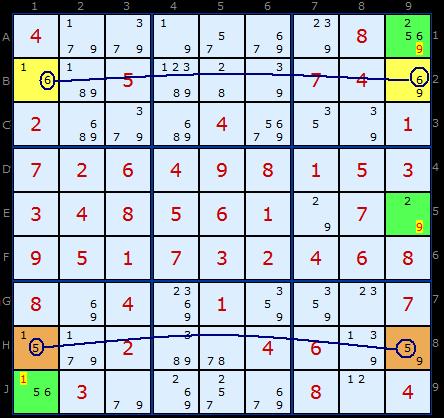
The logic goes as follows: 6 must occur in one of the two yellow cells and the 5 must occur in one of the brown cells. No doubt about that. But both 6 and 5 cannot occur in the same column. Lets pretend they do, say 6 and 5 in column 1. That would leave 9 as the only solution in two cells in column 9. Can't have that. So which ever way round 6 is 5 will be in the opposite column.

Multivalue X-Wing 1
Multivalue X-Wing 1: Load Example or : From the Start
This forces the 1 and 9 to fill the remaining two corners. If 1 and 9 are guaranteed to be in either a yellow or a brown cell apiece then we can't have any more 1s and 9s in those columns. Hence the eliminations.
The generalised X-Wing theory says that we can have a distorted X-Wing starting from 2 boxes and eliminating in 2 rows or 2 columns. This next example does just that. We have a strong link between the yellow cells (B7 and H7) using 5. And another strong link between brown cells (A9 and J9). Since the top pair share a box and the bottom pair also share a box we don't need exact row alignment.

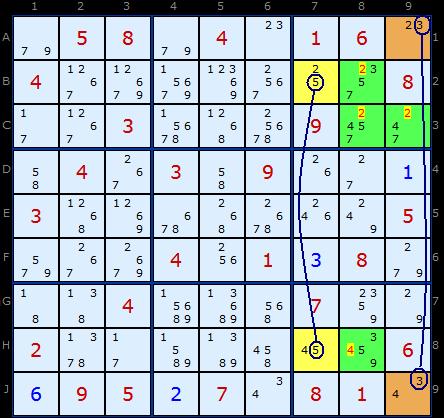
Using the arguement above we know that one 5 or 3 will occur in B7 or A9 forcing the other cell in the top right box to be a 2. We don't know which yet, but of those two cells will be a 2 so all the others in the box can go.

Likewise, a 5 or a 3 will appear one of the cells int the bottom box, H7 or A9. That forces 4 to be the solution to that pair - we just don't know which way round yet. The 4 in H8 can go.

 Multivalue X-Wing 2
Multivalue X-Wing 2: Load Example or : From the Start
Eliminations such as these can be achieved using Nice Loops and other very advanced strategies but this is well worth looking out for separetely since its both easier to spot and extends the elegance of the familiar X-Wing.




  
   
Comments

Your Name/Handle

Email Address - required for confirmation (it will not be displayed here)

Your comment or question

Please enter the
letters you see:
arrow		Enter these letters Remember me


Please keep your comments relevant to this article.
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted — no need to use <p> or <br> tags.


Comments - Talk

Sunday 5-Jun-2011

... by: David P Bird

Andrew the strong links you should be focusing on are those in the four bi-value cells in each example. In example 2 we get a sequence: (2'=3")r1c9 – (3'=4")r9c9 – (4"=5')r8c7 – (5'=2")r2c7 – Loop. Here all the odd(') or all the even(") numbered candidates will be true. This kills other 3s in c3, 4s in b9, 5s in c7 and 2s in b3, so it isn't necessary for 3 & 5 to be bilocal in the columns. You are therefore looking for an X-wing pattern made up of four bivalues with each side having a linking digit.

Andrew Stuart writes:

Quite right. I might change the focus of the search and strong links as you suggest and see if I get any extra hits with this search. I suspect that may still not produce enough extra value to bring it back into the solver - it is currently 'depciated' and unused. These results ought to pop out of several of the AIC and chaining strategies, but I'll need to do some testing. In the job queue.

Wednesday 1-Sep-2010

... by: p davis

a curiosity, but (7=2)D8-G8=(2-9)G9=F9 => F9<>7 solves the position immediately.

Monday 1-Feb-2010

... by: Steve

It seems to me that this strategy revolves around the two-candidate cells and does not really need the strong links. Pick any of the four cells and suppose that it solves to one of its candidates. This eliminates that candidate from one of the other cells, leaving it to solve to its other candidate. Continue in this way around the four cells, and you get the four values solving the four corners of the pattern. If you instead assume the other value solves the first cell, you can go the opposite way around to again find all four corners solved. And both ways put the same number in one or the other cell of each row and column. You can eliminate all four numbers from the rest of their rows and columns without any strong links required!

 Post a Comment using Facebook...


Article created on 11-April-2008. Views: 29248
This page was last modified on 12-April-2008, at 10:10.
All text is copyright and for personal use only but may be reproduced with the permission of the author.
Copyright Andrew Stuart @ Syndicated Puzzles Inc, 2011