SudokuWiki.org
Strategies for Popular Number Puzzles
Naked Candidates
'Naked' in this context refers to all the remaining possible candidates on a cell which are going to be used in a strategy. The simplest such situation is a Naked Single - or the last remaining candidate on a cell. Generally speaking, if you are making notes on a Sudoku board you have reached a point where simple scanning of the rows, columns and boxes has brought you no further solutions. But you will be finding plenty of Singles on the easier puzzles, and hopefully not too few on the hardest ones.
A Naked Single is exactly equivalent to saying "Ah Ha! Looking at that cell, I can see every other number either in the same box, the same row or the same column, so it's the only number that can fit."
Hidden candidates, mentioned below with regard to Pairs and so on, also have a Hidden Single equivalent. It occurs when you find a cell with lots of possible candidates, but you reason "well, X can't go anywhere else in either the row, column or box, so it must go here."
A Naked Single is exactly equivalent to saying "Ah Ha! Looking at that cell, I can see every other number either in the same box, the same row or the same column, so it's the only number that can fit."
Hidden candidates, mentioned below with regard to Pairs and so on, also have a Hidden Single equivalent. It occurs when you find a cell with lots of possible candidates, but you reason "well, X can't go anywhere else in either the row, column or box, so it must go here."
Naked Pairs
A Naked Pair (also known as a Conjugate Pair) is a set of two candidate numbers sited in two cells that belong to at least one unit in common. That is, they reside in the same row, column or box.
It is clear that the solution will contain those values in those two cells, and all other candidates with those numbers can be removed from whatever unit(s) they have in common.
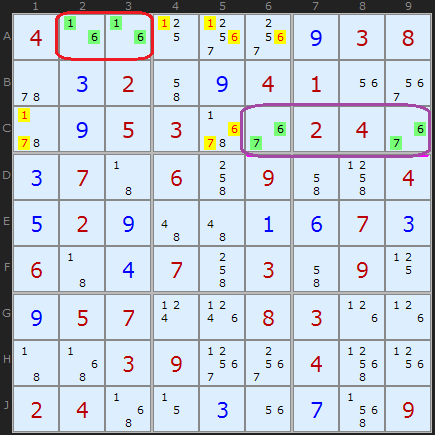
The [6,7] in row C is also a Naked Pair. It is aligned just in the row, but it removes three other candidate 6s and 7s in the row. Combining both Naked Pairs, we get a solved cell of 8 in C1.
There are other Naked Pairs at this point. You can identify them yourself or load the puzzle up in the solver to see them.
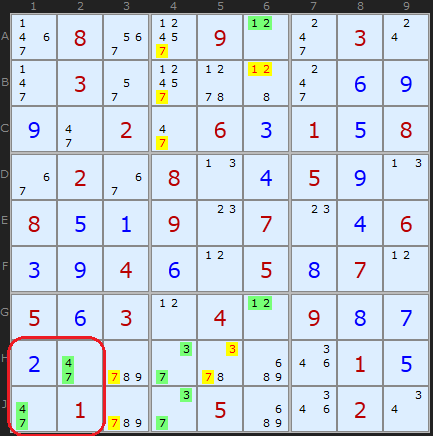
Just to show that pairs don't have to be aligned on a row or column, in this group of pairs we have a [4,7] pair on H2 and J1, which removes some 7s in the same box. Two other Naked Pairs eliminate further candidates at this stage.
Naked Triples
A Naked Triple is slightly more complicated because it does not always imply three numbers each in three cells.
Any group of three cells in the same unit that contain IN TOTAL three candidates is a Naked Triple.
Each cell can have two or three numbers, as long as in combination all three cells have only three numbers.
When this happens, the three candidates can be removed from all other cells in the same unit.
The combinations of candidates for a Naked Triple will be one of the following:
(123) (123) (123) - {3/3/3} (in terms of candidates per cell)
(123) (123) (12) - {3/3/2} (or some combination thereof)
(123) (12) (23) - {3/2/2}
(12) (23) (13) - {2/2/2}
The last case is interesting and the advanced strategy Y-Wing uses this formation.
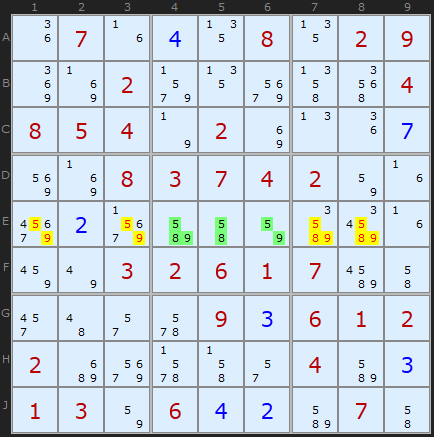
This first example is as straightforward as it gets. In row E, centre box, are the cells E4, E5 and E6 containing [5,8,9], [5,8] and [5,9] respectively. In total, those three cells contain [5,8,9], so we have fixed those numbers in those cells - just not which way round they will be. This allows us to remove those numbers from the rest of the unit the Triple is aligned on - namely the row.
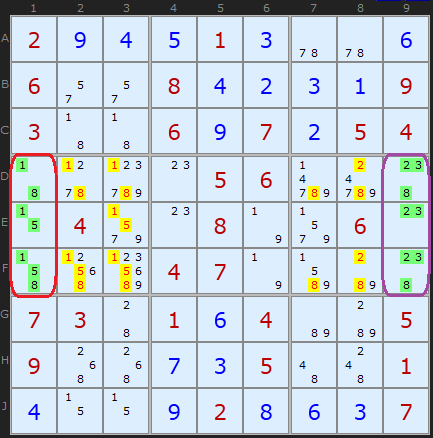
We have two Naked Triples at the same time on this board, in columns 1 and 9. There is no trickery in these Triples because the cells that form the triples are the last three unsolved cells in those columns - so they are bound to contain the three remaining values. Given that fact, we can clear out those values from each box containing a Naked Triple (and only the box, since there is nothing to clear off in the columns). But the manoeuvre nets us a great deal of candidates and we get a solution of 9 in F8.
In terms of the candidates per cell, the column 1 triple is a {2/2/3} formation (reading down) and the second, column 9, is {3/2/3}.
Naked Quads
A Naked Quad is rarer, especially in its full form, but is still useful if it can be spotted. The same logic from Naked Triples applies, but the reason it is so rare is because if a Quad is present, the remaining cells are more likely to be a Triple or Pair and the solver will highlight those first.
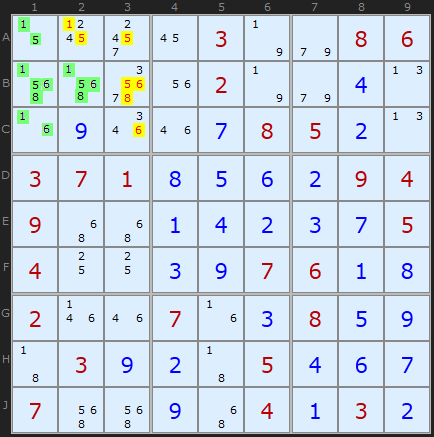
We don't consider higher orders of Naked candidates because there are only 9 cells in a unit. So if we were to suppose a "Naked Quin" with five candidates there would automatically be a complementary Quad since 5 + 4 = 9. Same point arises with Hidden sets, but it is worth noting that the Naked complement will be Hidden and the Hidden complement will be Naked. It may be viable to look for such beasts in 12x12 or 16x16 Sudokus.
Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Debbie Shayne
I am relatively new to Sudoku, but seem to be getting a decent handle on things. However, there is one thing that continues to stump me, and I almost certainly get it wrong each time, so I think there is something I am missing about naked triples. I hope I can describe it, since there seems to be no way to add a screenshot.
Let's say, in a unit, that I have the following candidates: (3,9) (3,4,9) (3,7,9) (3,4,7,9)...how do I know if the naked triple is (3,9) (3,4,9) (3,4,9) or (3,9) (3,7,9) (3,7,9)? I'm not sure if this is the best example, just one that is in a current game. It seems that I am constantly getting this type of pattern where it could go two different ways.
Thanks in advance,
Debbie
... by: Earl Zhu-Gallo
Thanks!
Earl
Taipei, Taiwan
... by: Stan
Maybe this particular example doesn't quite capture what I'm wondering about.
Is there a required sequence which, if not followed, could lead to trouble?
Process naked things before hidden things and pairs before triples, etc?
Also, is {1,2,3}, {1,4}, {1,5} a (potential) hidden triplet? I see triplets referred to as 3/3/3, 3/3/2, 3/2/2, 2/2/2 but never as 3/1/1.
Thanks for all your hard work.
No triples with {3,1,1}
... by: Silver
... by: John Short
Would you say therefore that it is unlikely to be able to complete the tougher puzzles without the solver at your elbow?
before using the solver I used to come unstuck occasionally and only find out when the last few steps remained. Then it was almost impossible to backtrack. The solver allows partial progress to be checked which is great. Very impressive piece of work
Depends. Most newspapers print relatively easy puzzles. Few require candidates everywhere. The solver is aimed at the tougher end and it's a long tail.
... by: George
... by: Janet
Janet D.
... by: Ing
... by: DanG
Thank you for the solver,
I don't fully understand all the strategies, but i'm working on it.
Although i like most of the examples shown,
The examples for the Naked Triples are not very useful.
Because the cells are align and it automatically exclude candidates.
I don't call that a strategy. It is more simple elimination.
We need to find examples where the cells are NOT align.
Have a nice day.
... by: Liz
I think the general rule is that in a unit with N solved cells, a naked n-tuple always has a complementary 9-minus-N-minus-n-tuple, but it could be naked or hidden. In your example above, with one solved cell, the 1568 naked quad reveals a 2347 hidden quad.
I have a conjecture that is sort of the converse: that any *hidden* tuple will always have a complementary *naked* tuple. I'm horrible at spotting hidden tuples unless I spot a complementary naked tuple. But although I've never seen an exception, logically I can't rule out the possibility that the complementary tuple might be hidden. Maybe I'm missing something obvious.
... by: David Ullman-Dougherty
There is a Sudoku board I would like you to look at
Click on this link
... by: Thomas
Sorry, I came here because I started to write a Sudoku solver and was wondering what inference rules it was missing (it's got hidden singles, naked * [because I enumerate all subsets], and pointing *). The first one I hit that it couldn't solve requires APE.
... by: Thomas
I only point this out, because it is a lot easier to program when you're thinking in subsets.
... by: Edwin
... by: bill drissel
Your bi-value illustrator shows me connections in a jungle of numbers but I'm too much of a novice to see how to use the connections. I never see a double line connection. What's the diff between strong and weak?
I'm really impressed by your work. When my wife began to work Sudoku, I was under the impression that mere tally work would solve anything. But I've found the puzzles much more subtle and demanding. Thank you for your excellent work.
Happy New Year,
Bill Drissel
Frisco, TX
... by: JohnNoneDoe
There is a Killer Sudoku board I would like you to look at
Click on this link
There will be a naked pair in b6,c7 linked by the cage starting at b6. That pair can eliminate candidates in b7. The solver seems not to see this.
... by: JohnF
A quick way to speed up the solver would be to check whether there are at least 8 unfilled cells in the row/col/box under examination - if there are not, then (as you point out) the solver would already have found a Hidden/Naked Triple or Double.
In fact you can take this one step further; if you have checked for a Naked Quad and not found one, then you won't find a Hidden Quad unless all nine of the cells are still unfilled.
... by: JWE
... by: David Spector
This situation is easy to find if you first find conjugate pairs, then see if they are on a row and column that intersect at a cell having two or more candidates.
Happens sometimes, not always.
... by: BabuYB
... by: Brian
... by: kasmar45
236 236 36
... by: Jan Bourdelle
In terms of the candidates per cell, the column 1's triple is a {2/2/3} formation reading down and the second is {3/2/3}.
... by: jb681131
... by: jeanne
... by: marmal9174
... by: Brian Fink
... by: Brian Fink
Let's say we have a chain of an overlapping even number of Naked Pairs, all the same pair, with two ends that can see a single cell but are not both aligned on the same row or column with it or even sharing the same box. Then the pair can be removed from that cell and only that cell, leaving all other digits in that cell as possibilities.
For example, if we had C1=3/7/8, C7=7/8, E7=7/8, and E1=7/8, then in addition to removing 7/8 from Row C and Column 7, you may remove it from C1 as well.
There may also be a variation of this that only includes a cell that can be seen by two cells with naked pairs (same pair) that are not part of a traditional Naked Pair, but I have yet to prove that one.
... by: Jan
But you do have one! In the Naked Triple example is also a naked quad for 2, 3, 8 and 9 in D9, E9, F9 and F8 (and so also a Hidden Quad for 1, 4, 5 and 7 in D7, D8, E7 and F7)
... by: Pete
It only took me a month to figure out.....
... by: Pete
Is it the case that each of the quad squares has to contain one number which appears in all 4 squares? If so, then how does this tie-in with the naked triple possibility of (12) (23) (13) ? Here, there isn't a number which appears in all 3 cells..
Great site btw
... by: KeithD
Eg, in the first triple example, try putting 5 in E1. Now E5 is 8 and E6 is 9, but E4 has no candidate.
... by: Simon
Can I make one small suggestion.
For each of the techniques (Naked singles, Naked candidates, Intersection removal, etc.)
you provide a couple of practice examples. for people to have a go at.
Thanks anyway.
... by: Tim
Why not G4 and G6
... by: Klaus
Thank You,
Klaus
BTY you have a great site, its so informative and I have learned so much from it, greatly appreciated.
... by: Roy
... by: Roy
... by: Roy
... by: Roy
... by: Anon
... by: Peter Rogers
What a fabulous website. This is what I have been looking for for years a real how to solve sudokus. I am stunned at its teaching capacity.
... by: gerhard, sweden
(example) 56, 67, 57, occuring in one row.
Let´s say that the bigrams occur in region 1 (bigrams 56 and 67) and in another region (57).
It is obvious that they work the same as any true triplet, but less obvious that the figure 6 can be eliminated from the remaining squares of region 1.
If this is described somewhere else, please excuse me for commenting.
... by: Pieter, Newtown, Australia
I always love to double-check my solution to a puzzle using your solver. I got this one by XY-Chains but damn it! I missed the naked & hidden Quads, yet again! I usually do, damn quads! :-(
I noticed you don't have an example for quads in your "Pick an Example" drop-down list. Want to include this one?
LOAD EXAMPLE
It's from the Sydney Sun-Herald of 2011-09-4 (Auspac Media for the puzzle). You may need to check with them re copyright.
Thanks as always for your great solver!
Ciao, Pieter
... by: Charlie R
... by: Dayanandan
Regards
Dayanandan
... by: hutch
many thanks for the obvious labor of love.
hutch
pawleys
... by: Andrew
"I notice that Sudoku Solver does not exhaustively identify all naked pairs as seen in the following puzzle.
http://www.sudokuwiki.org/sudoku.htm?bd=68050041905041000604160000000
9100040300700080400203960204871600000060104106000008
In row E the 2,5 pair in columns 3 and 7 should reduce cell E9 to just 1."
I don't understand why you say that. There's not such a naked pair there, and E9 has already a 3... Perhaps the sudoku saved with that id changed?
... by: Blaster88
... by: Rob Butler
... by: John
For example: (123) (123) (123)
Make any of the cells a 1: (123) (1) (123)
Drop 1 from the other cells: (23) (1) (23)
You can delete 1 from all other cells, because it is used. You can eliminate 23 from the other cells because it is a naked pair.
The same works for other triples: (123) (12) (23)
If the middle cell is 1: (23) (1) (23)
Eliminate 23 from other cells because it is a naked pair.
and so forth...
... by: Michael
A naked pair shows the same two values and only those values in two different fields (in the same column, row, or three by three square). This shows that those two fields each must have one of the two values (there are no other values to choose from). Since a value cannot occur more than once in any one column, row, or three by three square) the two values can be safely removed from the other clues since it is know that they must appear in the place of the naked pair.
Naked Triples and Quads simply extend the same logic to 3 and 4 values.
... by: Mike
http://www.sudokuwiki.org/sudoku.htm?bd=68050041905041000604160000000
9100040300700080400203960204871600000060104106000008
In row E the 2,5 pair in columns 3 and 7 should reduce cell E9 to just 1.
... by: Pete
... by: CS VIDYASAGAR
Thanks for keeping the aritcle simple and easily understandable.
... by: Harpo
... by: Werty
On the example.
imagine that you put 5 in one of the columns 2, 3 or 4. That will leave only 7 and 8 as candidates in three columns - 1, 8 and 9. Clear?
You will get to similar wrong position when you put 8 in column 4.
... by: Carol Kennedy
4,8 in a row then you can eliminate the other 4,8s in that row, but can I also erase all the other 4,8s in the column and the entire box as well? Thank you.
... by: Curt Klemenz
I suspect there is a mental algorithm for focusing attention toward the specific candidates, but no luck so far.
Anyone with a suggestion that's willing to share?
... by: Bruce D
... by: Rockmelon
Any suggestions??
... by: BobCarl
When there are only 3 different numbers that can fit into three of the nine cells, that automatically eliminates their use in the remaining six cells. Hence, they can be removed as candidates from those "other cells".
... by: buc