| Main Page - Back |
|
From SudokuWiki.org, the puzzle solver's site |
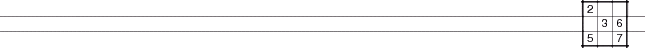
Naked Candidates
'Naked' in this context refers to all the remaining possible candidates on a cell which are going to be used in a strategy. The simplest such situation is a Naked Single - or the last remaining candidate on a cell. Generally speaking, if you are making notes on a Sudoku board you have reached a point where simple scanning of the rows, columns and boxes has brought you no further solutions. But you will be finding plenty of Singles on the easier puzzles, and hopefully not too few on the hardest ones.
A Naked Single is exactly equivalent to saying "Ah Ha! Looking at that cell, I can see every other number either in the same box, the same row or the same column, so it's the only number that can fit."
Hidden candidates, mentioned below with regard to Pairs and so on, also have a Hidden Single equivalent. It occurs when you find a cell with lots of possible candidates, but you reason "well, X can't go anywhere else in either the row, column or box, so it must go here."
A Naked Single is exactly equivalent to saying "Ah Ha! Looking at that cell, I can see every other number either in the same box, the same row or the same column, so it's the only number that can fit."
Hidden candidates, mentioned below with regard to Pairs and so on, also have a Hidden Single equivalent. It occurs when you find a cell with lots of possible candidates, but you reason "well, X can't go anywhere else in either the row, column or box, so it must go here."
Naked Pairs
A Naked Pair (also known as a Conjugate Pair) is a set of two candidate numbers sited in two cells that belong to at least one unit in common. That is, they are present in the same row, column or box.
It is clear that the solution will contain those values in those two cells, and all other candidates with those numbers can be removed from whatever unit(s) they have in common.
The [6,7] in row C is also a Naked Pair. It is aligned just in the row, but it removes three other candidate 6s and 7s in the row. Combining both Naked Pairs, we get a solved cell of 8 in C1.
There are other Naked Pairs at this point. You can identify them yourself or load the puzzle up in the solver to see them.
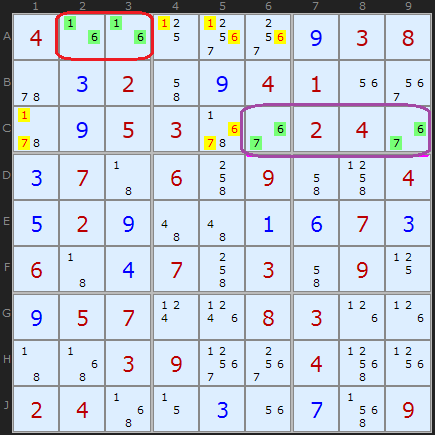
Just to show that pairs don't have to be aligned on a row or column, in this group of pairs we have a [4,7] pair on H2 and J1, which removes some 7s in the same box. Two other Naked Pairs eliminate further candidates at this stage.
Cage Naked Pairs
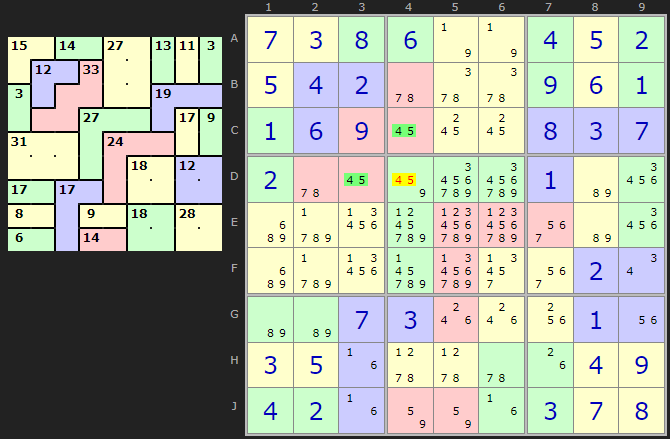
As Sluggy points out in the comments there are additional ways Naked Pairs can influence puzzles beyond vanilla Sudoku. The Killer Solver will identify Naked Pairs in a cage - and if the configuration of cells permits - there may be other cells that the pair can reach. C4 and D3 share no row, box or column but they do share a cage. Since 4 and 5 must be present in those two cells we can remove 4 and 5 from D4.

Naked Triples
A Naked Triple is slightly more complicated because it does not always imply three numbers each in three cells.
Any group of three cells in the same unit that contain IN TOTAL three candidates is a Naked Triple.
Each cell can have two or three numbers, as long as in combination all three cells have only three numbers.
When this happens, the three candidates can be removed from all other cells in the same unit.
The combinations of candidates for a Naked Triple will be one of the following:
(123) (123) (123) - {3/3/3} (in terms of candidates per cell)
(123) (123) (12) - {3/3/2} (or some combination thereof)
(123) (12) (23) - {3/2/2}
(12) (23) (13) - {2/2/2}
The last case is interesting and the advanced strategy Y-Wing uses this formation.
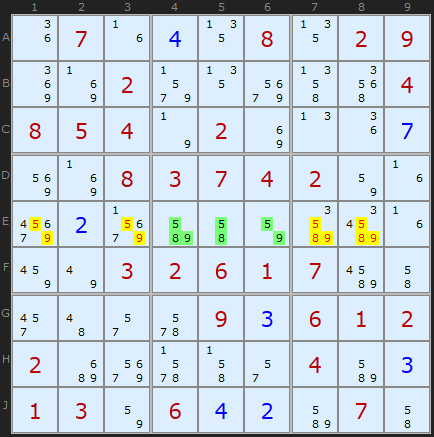
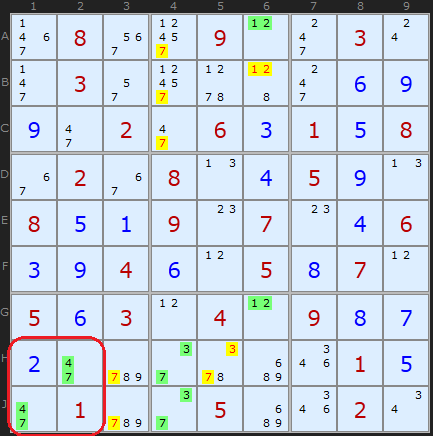
This first example is as straightforward as it gets. In row E, centre box, are the cells E4, E5 and E6 containing [5,8,9], [5,8] and [5,9] respectively. In total, those three cells contain [5,8,9], so we have fixed those numbers in those cells - just not which way round they will be. This allows us to remove those numbers from the rest of the unit the Triple is aligned on - namely the row.
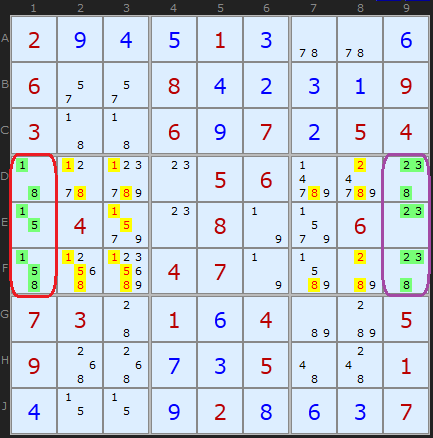
We have two Naked Triples at the same time on this board, in columns 1 and 9. There is no trickery in these Triples because the cells that form the triples are the last three unsolved cells in those columns - so they are bound to contain the three remaining values. Given that fact, we can clear out those values from each box containing a Naked Triple (and only the box, since there is nothing to clear off in the columns). But the manoeuvre nets us a great deal of candidates and we get a solution of 9 in F8.
In terms of the candidates per cell, the column 1 triple is a {2/2/3} formation (reading down) and the second, column 9, is {3/2/3}.
Naked Quads
A Naked Quad is rarer, especially in its full form, but is still useful if it can be spotted. The same logic from Naked Triples applies, but the reason it is so rare is because if a Quad is present, the remaining cells are more likely to be a Triple or Pair and the solver will highlight those first.
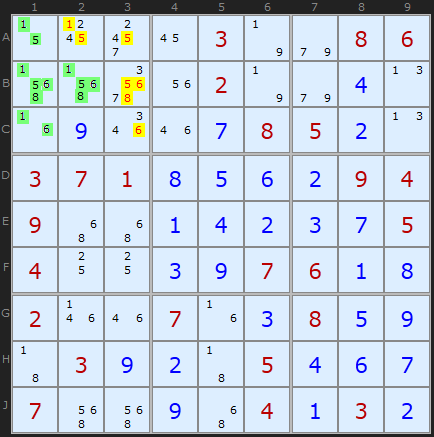
We don't consider higher orders of Naked candidates because there are only 9 cells in a unit. So if we were to suppose a "Naked Quin" with five candidates there would automatically be a complementary Quad since 5 + 4 = 9. Same point arises with Hidden sets, but it is worth noting that the Naked complement will be Hidden and the Hidden complement will be Naked. It may be viable to look for such beasts in 12x12 or 16x16 Sudokus.