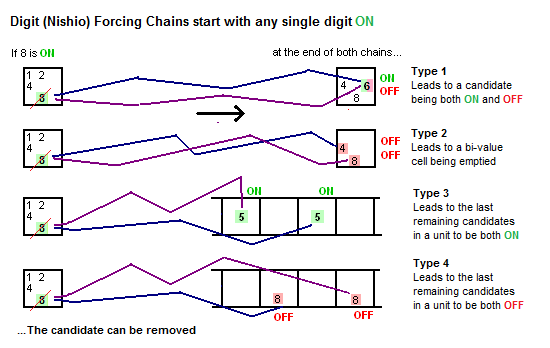
Nishio Forcing Chains

Nishio has a long history in the community as a semi 'trial and error' approach to very hard Sudoku bottlenecks, but in the implementation on this website it fits very nicely into the family of forcing chains and is a formal 'pattern' based strategy that uses AICs. In fact it is very close to Digit Forcing Chains since Nishio works on a single candidate as well. Where Digit Forcing Chains take a candidate and consider the consequences of the candidate being both ON and OFF, Nishio tries to find a contradiction when the candidate is merely ON. Two chains emanate from the candidate in different directions and try to join up later on another candidate. The rule is, if the start candidate is ON and this leads to another candidate being both ON and OFF it is indicating an impossible state of affairs. So the original candidate cannot be a solution.

A Nishio forcing chain is sometimes the exact reverse of a Digit Forcing Chain. If you look at the first diagram on that page you'll notice the first 'type' in the set of four ways a contradiction can be found is a destination candidiate that is ON when the start candidate is both ON and OFF.

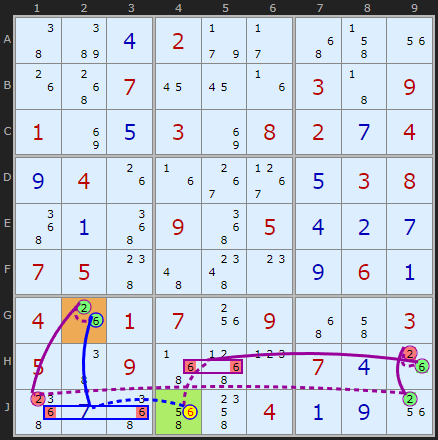
Nishio Forcing Chain example : Load Example or : From the Start

In this example the starting candidate is 6 in J4. The shorter blue chain simply says that when 6 in J4 is ON it removes the 6s in box 7 leaving 6 in G2 as the only remaining 6 and therefore the solution. On the other hand, the longer purple chain implies 6 cannot be the solution in G2. A 6 in J4 means 6s are removed from the rest of box 8 and that turns ON the six in H9. That forces 2 in J9 which in turn removes 2 from J1 making G2 2 and not 6.

Therefore the 6 in J4 cannot be a solution and it can be removed.

Go back to Digit Forcing Chains

Continue to Cell Forcing Chains

Comments

Please ensure your comment is relevant to this article.
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.

CommentsTalk

... by: tebo

Sunday 17-Sep-2023

Why does Laren state that "This Nishio chain is also a Discontinuous Nice Loop type 3"? As I see it, Nishio is the joining of two AIC segments (or Nice Loop segments) at two nodes of discontinuity. Nice Loops allow for only *one* node of discontinuity. Where is the discussion of Nice Loops? Also, where is the discussion of "weak-weak loop" (Ghost 2T)?

REPLY TO THIS POST

... by: Ghost 2T

Saturday 7-Jan-2023

The above example is the same as "weak-weak loop", type 1 at J4.
You can combine the TH supposes the series to the same article, divide it into many articles for what. (Because of the principle it is the same "true/false 1 -> true/false 2")

REPLY TO THIS POST

... by: Leren

Friday 17-Aug-2012

This Nishio chain is also a Discontinuous Nice Loop type 3 - but for some reason your solver bypasses this AIC strategy. The solver's choice of Nishio chains also seems somewhat arbitrary - you could just as easily transfer the required contradiction to any of the cells in the loop. Also the graphic is a bit confusing - the 6 in G2 should be coloured green to highlight the contradiction in that cell (2 candidates both coloured green). Are there cases where Nishio chains are not also Nice loops?

Andrew Stuart writes:

Correct on the connection with Discontinuous Nice Loop type 3. The green cell highlight I think is a carry over from previous strategies where I mark the end of the chain. Probably not necessary. The final candidate 6 in G2 is yellow as that follows the graphical convention of showing eliminations in yellow/red text. It would be green if it was part of the chain.

The solver returns the first instance of the strategy used but currently cant cycle through all instances of that strategy so I'm sure other formations of the same chain are possible as it's also a loop. I'd like to allow that in the solver and it's an upgrade I have in the job queue. There is a limit on the length of normal single chain AICs which I have to impose to stop the program taking too long to return (mainly for the grading feature which has to run through all the strategies). That means that some AICs might not be found and instead two chains in the double chain strategies like Nishio get to find the same result as each chain is under the limit. I've had several goes at optimising the AIC searchs but not to any great improvement in speed.

I haven't broadened Nishio to non loop type entities because the narrow definition I've worked with has start and end points on single candidates. But I'll be the first to admit there is overlap with other chaining strategies.

Add to this Thread