Very powerful elimination sets can be deduced from the overlap of two Exocet patterns. In the current solver implementation the two Exocets need to contain the same Base candidates but Double Exocet is known to be wider that that and I hope in the future to take into account Exocets that only partially overlap.

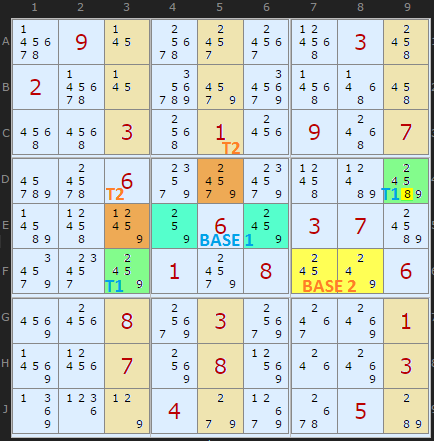
Here is a great example from Unsolvable #165. The blue/green cells identify Exocet 1 and the yellow/orange cells mark Exocet 2. Base and target cells are marked and labelled. A glance at these cells will tell you that the Base candidate set for both Exocets is {2,4,5,9}.

The S-Cells for both Exocets are also the same, so I've not attempted to color them individually.

Considered on their own I can find only one elimination:
Elimination rule 1: 8 removed from target cell D9

For the first elimination rule we consider all four target cells together as one unit. And the same for all four base cells. I have colored those cells pink and blue in the second diagram.

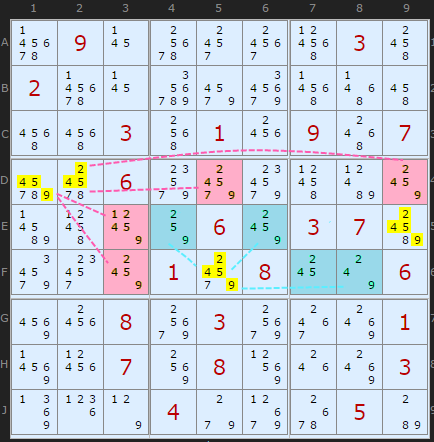
Rule 1 says that 'known' base digits that see all four target cells or all four base cells can be removed. So any of {2,4,5,9} in D1 and D2 can be removed - pink dashed lines show they can see all the target cells. Likewise F5 can see all base cells (blue dashed lines). So can E9.

David Bird's definition includes the word 'known' when looking at base candidates. 'Known' means that they must fit somewhere in the target+base cells where otherwise they could still be ambiguous. This hints at the partially overlapping wider definition of Double Exocet but since in our example the overlap is entire all base candidates are 'known'. When I have fully implemented Exocet I'll be able to make this condition more explicit.

Now, we are not done yet with this example. Lets consider next the importance of the S-Cells and their covers. These were important in making sure the Exocet pattern really existed. Since we have two Exocets with the same base candidates some very severe restrictions on the distribution of {2,4,5,9} exist.

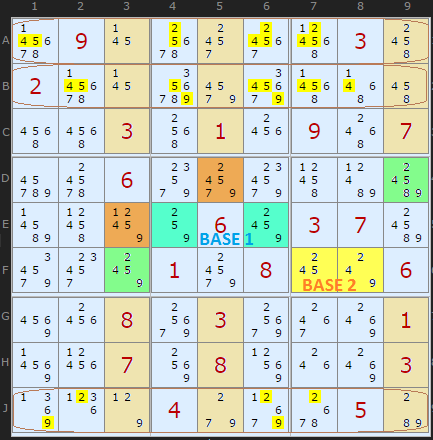
Rule 2 says that known base digits in non-'S' cells in their cover houses canbe removed.

So we have checked to see if {2,4,5,9} exist no more than twice in all the S-Cells and that gives us our three cover-lines - rows A, B and J. Basically, our base candidates must be true on somewhere along those S-Cell columns so there is simply no more room for them in those rows. There are strong echos here with the Swordfish strategy.

Instead of picking through a dozen lengthy chaining strategies this single step blows the puzzle wide open and its singles all the way to the end.

There is still much more to consider with Exocets and Double Exocets and I hope to master the finer points and additional rules to further improve the solver.