SudokuWiki.org
Strategies for Popular Number Puzzles
X-Cycles
X-Cycles are the start of a large family of 'chaining strategies' which are fundamental to solving the harder Sudoku puzzles. X-Cycles are strongly related to Simple Coloring.
A 'chain' is a series of links hopping from one candidate to another following very simple rules. A candidate can either be ON or OFF. That is, we either think it is a possible solution to that cell, or we do not. There are consequences to the rest of the board when we 'link' these two states.
A 'chain' is a series of links hopping from one candidate to another following very simple rules. A candidate can either be ON or OFF. That is, we either think it is a possible solution to that cell, or we do not. There are consequences to the rest of the board when we 'link' these two states.
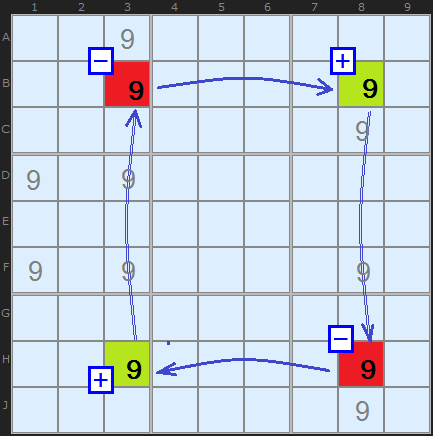
In the X-Wing structure in Figure 1, as an example, we can consider B3 to be OFF. This forces the the 9 in B8 to be ON since it's the only remaining 9 in the row. If B8 is ON then that removes the 9 in H8. Again, the consequence is to turn ON the 9 in H3 - and that closes the loop by confirming the 9 in B3 is OFF.
In this X-Wing example three things are apparent. I went round clock-wise, but I could easily make the same logical chain going round from B3 to H3 to H8 to B8 and back to B3. Also, could decide that the start cell was ON and follow the loop round. And lastly, B3 is arbitrary, I could start on any of those four cells.
Another important way of thinking about this situation is from the point of view of the links. When a candidate is turned OFF AND there are only two candidates in the unit, then we can create a Strong link, as between B3 and B8 (marked in a thick blue line) and H8 and H3. Because there are just two 9s in each row, we know that if one is not a 9, the other must be. A strong link is where:
!A => B (if not A, then B)
Weak links are the opposite:
A => !B (if A, then not B)
Strong and Weak links alternate just as candidates are turned OFF and ON. When we turn a candidate X ON we effectively remove ALL other candidates of X in ALL other units. However, when we turn a candidate X OFF it has no effect unless the unit has only two of X in it.
!A => B (if not A, then B)
Weak links are the opposite:
A => !B (if A, then not B)
Strong and Weak links alternate just as candidates are turned OFF and ON. When we turn a candidate X ON we effectively remove ALL other candidates of X in ALL other units. However, when we turn a candidate X OFF it has no effect unless the unit has only two of X in it.
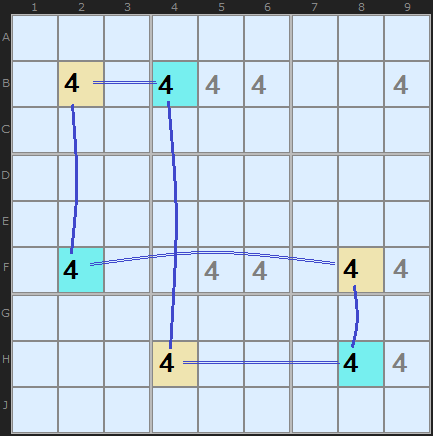
A "Cycle", as the name implies, is a loop or joined-up chain of single digits with alternating strong and weak links, as the X-Wing in Figure 1 shows.
In Figure 2, we have a 2-2-2-formation Swordfish re-drawn to show the strong and weak links. The loop characterises the X-Cycle, and the strong/weak links alternate.
Nice Loops have evolved a notation which is useful when accompanying a diagram or as part of an explanation. X is, of course, the digit, and we use the row letter and column number notation to identify cells (e.g., B2, F8). The cells in the loop are linked with a minus to indicated X has been turned OFF, and a + to indicated X has been turned ON - you will see these colours on the solver. An example:
+x[cell 1]-x[cell 2]+x[cell 3]-x[cell 4]
The 2-2-2 Swordfish above can be expressed as:
+4[B2]-4[B4]+4[H4]-4[H8]+4[F8]-4[F2]
The only thing not explicit in this notation is that the last cell joins back onto the first cell. Thus, 4[F2]+[B2].
Loops can be of any length but they don't re-use any candidate.
Chains like these that go in a loop are called Continuous. They have three characteristics:
Even with the convention of starting with the top left-most cell, there are four ways we could write down a chain:
I've deliberately used neutral colours in the diagram above (yellow and blue) not to given the impression there only one way to write the same chain. However, the solver will return very positive red and green highlighting but that's because it has discovered one of those four ways first and discarded the other three identical ways.
+x[cell 1]-x[cell 2]+x[cell 3]-x[cell 4]
The 2-2-2 Swordfish above can be expressed as:
+4[B2]-4[B4]+4[H4]-4[H8]+4[F8]-4[F2]
The only thing not explicit in this notation is that the last cell joins back onto the first cell. Thus, 4[F2]+[B2].
Loops can be of any length but they don't re-use any candidate.
Chains like these that go in a loop are called Continuous. They have three characteristics:
- Firstly, it doesn't matter which way you walk round the loop - clockwise or anti-clockwise
- Secondly, it doesn't matter which cell you start with (although the convention is to start with the top left-most cell)
- Thirdly, each cell could be ON or OFF - as long as you alternate.
Even with the convention of starting with the top left-most cell, there are four ways we could write down a chain:
- Clockwise with B2 ON +4[B2]-4[B4]+4[H4]-4[H8]+4[F8]-4[F2]
- Clockwise with B2 OFF -4[B2]+4[B4]-4[H4]+4[H8]-4[F8]+4[F2]
- Anti-clockwise with B2 ON +4[B2]-4[F2]+4[F8]-4[H8]+4[H4]-4[B4]
- Anti-clockwise with B2 OFF -4[B2]+4[F2]-4[F8]+4[H8]-4[H4]+4[B4]
I've deliberately used neutral colours in the diagram above (yellow and blue) not to given the impression there only one way to write the same chain. However, the solver will return very positive red and green highlighting but that's because it has discovered one of those four ways first and discarded the other three identical ways.
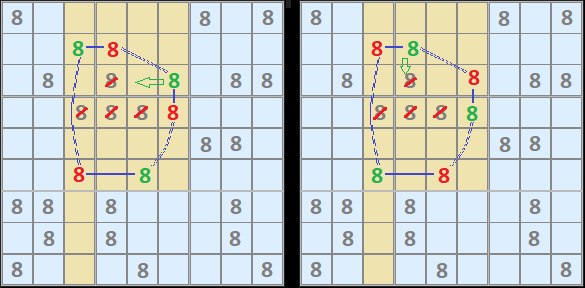
In this example of an 8-Cycle in Figure 3, I have split the two possible states into two diagrams.
This shows how each pair of strong links (that have only two candidates in the shared unit) can be set overall. No other combination of ONor OFF is possible.
The notation can either be, left
+8[B3]-8[B4]+8[C6]-8[D6]+8[F5]-8[F3]+8[B3]
or right
-8[B3]+8[B4]-8[C6]+8[D6]-8[F5]+8[F3]-8[B3]
The yellow cells are units where other 8s can be eliminated, which in this case correspond to the third column and boxes 2 and 5 because that's where the weak links are located. C4 is eliminated because of either B4 or C6
Nice Loops Rule 1
Nice Loops that alternate all the way round are said to be 'continuous', and they must have an even number of nodes. With a continuous X-Cycle, candidates are not removed from the loop since the loop does not have any flaws. Instead we are looking to eliminate on the units that can be seen by two or more cells that belong to the loop.
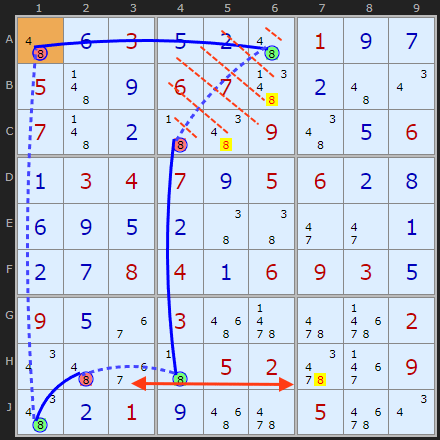
Figure 4 is a real-life example of an X-Cycle based on 8. The cells with links are in red and green. We can immediately see that C2/C7 is a weak link across the row because of the 8 in C3. G2/H3 is also a weak across the box because of the third 8 in G3. The last weak link is in box 9, J7/H9. Any other 8s in these units can be removed, which makes it a powerful technique. We end up with a loop containing only strong links – a result identical to a Colouring (Simple Colouring) solution.
The output from the solver will contain the following information:
X-CYCLE (Alternating Inference Chain):
+8[C2]-8[C7]+8[J7]-8[H9]+8[H3]-8[G2]+8[C2]
- Off-chain candidate 8 taken off C3 - weak link: C2 to C7
- Off-chain candidate 8 taken off C9 - weak link: C2 to C7
- Off-chain candidate 8 taken off G9 - weak link: J7 to H9
- Off-chain candidate 8 taken off G3 - weak link: H3 to G2
In summary we can see that
Although there are many other parallels as well.
- X-Wing is a Continuous X-Cycle with the length of four.
- Swordfish of the 2-2-2 formation is a Continuous X-Cycle with the length of six.
Although there are many other parallels as well.
This very attractive Nice Loop with off-chains is from Denis Berthier's supplements to The Hidden Logic of Sudoku, a web page I can only find on the Internet Archive. It is the Second Whip Example - a beast of a puzzle. I have been trying to understand what these are all about (and struggling). Apparently Nice Loops are an old-fashioned way of thinking about such things. Berthier breaks this one up into NRC chains (or "Not Rule out Candidates"). I implemented an NRC alternative to loops quite some while ago but since it was memory intensive I've not thought it suitable for the online solver. Only marginally more efficient. Going to have to cover Whips and NRC chains soon.
Part 2 ...
This article continues - for documentation on discontinuous Nice Loops click HERE
Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Gere
I am trying to learn more about solutions for Sudokus. I am really a newbie.
Is it necessary that a strong link is always followed by a weak link, or can two strong links follow each other?
You might not have read as far as this page: Weak and Strong Links
Which I hope will set everything straight regards the two types of link
... by: Ed Logg
..3...9.11967..5.....19..6....479613.19...7.83.78.129..71945..6..5.871.99..61....
proceed until you get to the xy-chain. Notice you missed the x-cycle case 3 with 5 at E8 F9 F5 E4 A4 A5 that eliminating the 5 at F5, I suspect that is because you took the branch at F9 to J9 and J8 without going back and trying the F9-E8 strong link.
... by: Jim
You have a great site - I have learned a lot. It seems to me there is a slight bug in one of the Simple Coloring examples (the one with 2...41..6 in row A). After the 4th SC there is an X-Cycle, but the link from E9 to F8 is a strong link, not a weak link as shown. So it isn't a true X-cycle with 3 strong links in a row, or am I missing something? The puzzle solves OK, and if you remove the X-Cycle check box, the puzzle also solves using an XY-Chain.
Thought you would want to know.
Best
... by: Jim
Keep up the excellent work, your illustrations are second to none
... by: Arno
Near Fig.1 example, you wrote "Also, could decide that the start cell was ON and follow the loop round." But, in this case (startcell B3 ON), then B8 is off, but it will not mean that H8 is ON (B8-H8is weak link), so chain is not built.
I think that you can't go any direction (cw ot ccw) with both states (ON/OFF) on start cell:
If start cell is OFF, it must go thru a strong link; and if start cell is ON, then the first move should be thru a weak link.
If you agree with this, the 4th paragraph near fig.1 should have more restrictions, since it's little confusing.
... by: Justin
Sorry if this is a sill question. I really enjoy studying these strategies and consider your site to be excellent. I have spent many hours on it and have recommended it to friends, who are similarly impressed with it.
I have re-drawn Figure 3 and added some more text, to be more clear.
... by: britanico
Refering fig. 2 :nice loop on 4 it seems to me you can't start B2 OFF clockwise as you have a weak link to B4, that must start with ON state to provide any inference.Only if there's a strong link can then B2 start with a OFF state, clockwise.
Please, continue your good work and thank you for your kind attention.
... by: Kavala
X-Cycle
X-CYCLE on 2 (Discontinuous Alternating Nice Loop, length 6):
+2[C7]-2[C5]+2[E5]-2[E8]+2[F7]-2[C7]
- Contradiction: When C7 is set to 2 the chain implies it cannot be 2 - it can be removed
I follow this but I see only five links and five nodes. Except you count the start and end nodes, which are the same, as two nodes ?
... by: Ian
... by: Bob Rodes
... by: Buzz
Been away for a while--Frank Longo put out his follow up to the Mensa books - titled "Beyond Black Belt Sudoku"--- I bought it--puzzles really quite easy though-- 300 puzzles-- I have only completed around 20 so far--randomly chosen from 1 to 300--- but strategies like rectangles, x- wings, XY chains, Y- wings, X-cycles, XYZWINGS, ETC-- are about all you need--
Have not run into a single one yet that needed forcing chains etc etc -- I understand the forcing chain strategies but fail to be able to recognize them when they are present--maybe that is part if the intended fun--- like looking and the thinking
AT ANY RATE-- as I have told you before-- doing the basics-- singles, pairs,triples, box line reduction, pointing pairs etc etcetc is so damn boring I let the Solver do all of that--Then I print and solve the puzzle--
Soooooooooo
--First-- can you make an "auto button" to take any puzzle through the basics rapidly so that you do not have to keep tapping "take step"--- which is what I do -- until I get to no solutions ( all other strategies I have turned off-- thanks to your "off" buttons) -- then I print and enjoy looking for those strategies that will solve
-- Next--since I do the above for all puzzles no matter where I get them from---CAN YOU PUT A BOX ON THE PUZZLE WHICH SHOWS UP AFTER YOU SELECT THE PRINT BUTTON--- that WILL ALLOW YOU TO IDENTIFY THAT PUZZLE
-- for example--a comment box-- or puzzle name box-- for things like date, where puzzle from, number of puzzle, etc etc-- that will be on the print out?
Hope your well --love the site-- studying the BUG STRATEGY-- new to me--
Cheers,
Buzz
As of 2025: Hover your mouse over the title on the print page - it will allow you to edit it.
... by: Mike Van Emmerik
What am I missing?
However, it seems to me that it can be solved with a simple extension of the simple-colouring technique. If you start on a particular square and end up on that same square at the end of a strong link (with an odd square count, starting as I do with zero), then it seems to me you have a Discontinuous Alternating Nice Loop situation, and the candidate in question (in this case, an 8) must be the solution, so other candidates in the start/end cell (in this case, one candidate, a 6) can be eliminated. I'll grant you that this is enough different from simple colouring to warrant a separate name.
I maintain however that all the other situations where the X-cycle has found the "first" solution, should have been found by the simple colouring solver.
I also note that simple colouring can be extended to grouped simple colouring, so the same comments apply to the grouped X-cycles. As a result, I don't believe that grouped X-cycles deserve to be in the "extreme" strategy category.
I'm guessing that the naïve belief that a small group of general strategies (like simple colouring) can solve almost all Sudoku problems happens to most beginners like me :-O
... by: snaponit
MONDAY 26-NOV-2012
... by: Hilary
Your site is very helpful. The main problem I have with the puzzles that require diabolical strategies is that I don't know how to pick 'x' for the x-cycle for example. So I usually pick 'x' at random. But to me, that's trial and error and I was wondering if you had suggestions for a systematic approach
Thanks !
... by: Hilary
Thanks !
As a preface, I would note that dead-ends are what consume time and differentiate the best from the competent players,and so knowing when to try a strategy, and what number to try it with first, and how to ignore obviously dead end paths within a strategy, are all key to the highest level play. E.g., in today's Sudoku, reviewing the puzzle post hoc using the automated solver showed the automated skipping many early to mid-level strategies, jumping instead to a chaining strategy early. The overarching question is how one knows the direction to take at each decision point, so all dead-ends are not attempted. How does one know, at a glance, to skip early listed strategies, and within each, know when to punt, rather than continue with a strategy will in the end not be productive?
The specifics for this strategy, per Hilary (in part): It is not at all clear [1] what it is about the appearance of the board that suggests it might actually be time to choose a chaining strategy attempt, [2] relatedly, how you choose the actual number to begin the attempt, [3] where on the puzzle it is best to begin the attempt—how to choose a starting point, and [4] what it is, subtly, about a particular direction, that clues one in to going in that direction.
Then, aggravatingly—and here, cut-and-paste and expand upon existing text if this statement indicates I have missed what you believed to be an already clear, existing bit of teaching—it is not always at all clear, during the course of creating chains, why at each given node you proceed to the particulate next match that you choose. The rampant selections between alternative directions that could be taken in Figure 4 (and less easily seen, in the three preceding figures) make clear you are making decisions based on criteria that are unspoken (perhaps of which you a re unaware). (The statement "We can immediately see that C2/C7 is a weak link across the row because of the 8 in C3." is an example of an over simplistic summary of several logical steps that you are applying in deciding the course of creating the chain. Etc.)
Bottom line, I find I can easily understand the explanations of the strategies I already understand, or have independently hit upon, but when I wish to understand a completely novel strategy that you present, it is near impossible, using your text alone, esp. with regard to understanding the full sequence of choices (next steps ignored over next steps taken) that you make to end up with a chain that you present. Better one simpler example, with thorough and complete decisions at each node, presented absolutely clearly, than a series of more complex examples presuming "facts not in evidence" (basic understanding not really in place). [LeProf]
... by: Dolores
-5[E8]+5[J8]-5[J7]+5[B7]-5[A6]+5[A4]-5[E4]+5[E8]
- Contradiction: When 5 is removed from E8 the chain implies it must be 5 - other candidates 2/4/8/9 can be removed
Also, how do you choose which 5's to include and which to exclude in the chain. Because most of the squares had a 5.
Basically, if 5 is removed the knock on effect - if you trace it all the way round the chain - is that 5 is put back in that starting place - which is a contradiction. So we can deduce 5 must be the solution to that cell and we can remove everything else.
... by: Cathy
... by: JimS
Maybe Andrew answered your question privately or maybe it is posted somewhere else on this site but I thought that I would try to answer your question.
As you follow a continuous, alternating nice loop along the path some of the weak links can actually be strong links -- they just don't have any digits that can be eliminated. Imagine an X Wing which only has digits that can be eliminated in one unit not two.
Andrew might be more accurate if he said "weak or strong links" instead of just "weak links" but that would be cumbersome and wouldn't really help the understanding of the concepts.
Hope this helps.
... by: Laura
... by: ECC
... by: Elleda Katan
[1] In none of the x-cycle demos is the digit removed from the cells forming the loop. Instead it is eliminated " from cells that can be seen by two or more [loop] cells." In the 4/5 puzzle 7 is eliminated from E1, the beginning and end of the loop.
[2] The end result says your explanation is a loop containing strong links. However, in 4/5, eliminating 7 from E1 destroys the loop.
[3] In the documentation under the 4/5 puzzle, the loop is described as : 7[E1]-7[E4]=7[J4]-7[J3]=7[G1]-7[E1] "Discontinuity is two weak links joined……" However, 7[G1] to 7[E1] is a strong link, not a weak one, no? Shouldn't it read : 7[G1]=7[E1]?
Please I love love love your puzzles and am trying to get smarter at understanding the more advanced strategies, but this confusion has me X-ing out x-cycles from solutions because I am so baffled by them. Thank you for your time.