XY-Chains
XY-Chains is a way to connect two parts of the board that can't directly "see" each other. The "X" and the "Y" in the name represent these two values in each chain link. If we can connect the ends we can make inferences and eliminate candidates.
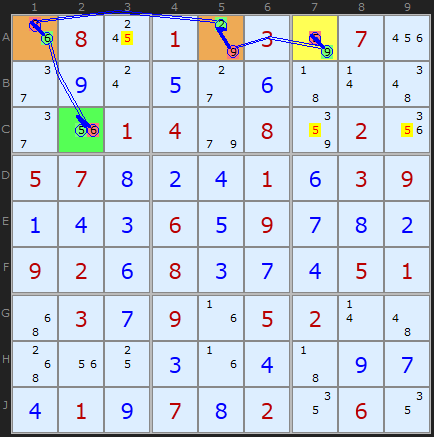
The example here is a very simple XY-Chain of length 4 which removed all 5's highlighted in yellow. The chain ends are 5 A7 and C2 - so all cells that can see both of these are under fire. It's possible to start at either end but lets follow the example from A7. We can reason as follows
- If A7 is 5 then A3/C7/C9 cannot be.
- if A7 is NOT 5 then it's 9, so A5 must be 2, which forces A1 to be 6. If A1 is 6 then C2 is 5.
Which ever choice in A7 the 5's in A3/C7/C9 cannot be 5. The same logic can be traced from C2 to A7 so the strategy is bi-directional, in the jargon.
This strategy cannot predict which end of the chain will have the solution 5 just that at least one end will do so. Testing on a large set of puzzles (>10,000) reveals that in 57% of XY-Chains found the solution is at both ends of the chain.
This strategy cannot predict which end of the chain will have the solution 5 just that at least one end will do so. Testing on a large set of puzzles (>10,000) reveals that in 57% of XY-Chains found the solution is at both ends of the chain.
Chain Notation
The solver uses relatively simple chain notation with cells identified with [Row Letter+Column]. (There is an option to change to rYcX coordinates). In a chain we're alternating between strong and weak links but also turning candidates ON and OFF. To symbolise that the chain uses plus and minus. The number being turned on or off follows the symbol. The above example is
-5[A7]+9[A7]-9[A5]+2[A5]-2[A1]+6[A1]-6[C2]+5[C2]
5 taken off A3
5 taken off C7
5 taken off C9
In later documentation on Grouped X-Cycles you will see grouped cells denoted as +4[D4|E4] and when ALSs are used to make a link curly brackets are used: +7{H6|G6}. Rare exotic links like Unique Rectangles are named -9(UR[DF28]) as is an X-Wing -8(XW[-E3/-B3+B2-E2])
-5[A7]+9[A7]-9[A5]+2[A5]-2[A1]+6[A1]-6[C2]+5[C2]
5 taken off A3
5 taken off C7
5 taken off C9
In later documentation on Grouped X-Cycles you will see grouped cells denoted as +4[D4|E4] and when ALSs are used to make a link curly brackets are used: +7{H6|G6}. Rare exotic links like Unique Rectangles are named -9(UR[DF28]) as is an X-Wing -8(XW[-E3/-B3+B2-E2])
Example 2
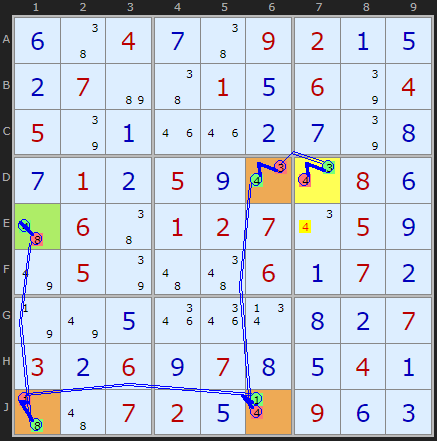
This relatively easy Sudoku puzzle contains contains a nice XY-Chain near the end. It proves 4 must be in either E1 or D7 and therefore we can remove the 4 in E7 since that cell can see both ends.
Detection Changes August 2025
XY-Chains go way back to the earliest instance of the solver and had separate code for this strategy because the pattern is very simple and it pre-dates my work on AICs. But the selection of the “best” XY-Chain was very crude. I’d look for length 3 and return the first, then any length 4 and finally any length 5-12 and return the first. (Length here is the number of cells, not the chain links which are double the 'length').
I decided to see if I could use the AIC code to look for this pattern and re-use some code. The AIC Chain detection builds a list of the best 50 chains and allows the solver to “explore” other chains at the same step. This means XY-Chains share the same priorities: number of eliminations before length, length before same number of eliminations and so on. Same preference order as AIC and other chaining. This may change the score and solve order of puzzles that require XY-Chains.
Also the old XY-Chain code was not using Windoku and Sudoku X diagonal units which was a big miss.
Currently XY-Chains do not use exotic links as this would turn a 'diabolical' strategy into an 'extreme' one.
I decided to see if I could use the AIC code to look for this pattern and re-use some code. The AIC Chain detection builds a list of the best 50 chains and allows the solver to “explore” other chains at the same step. This means XY-Chains share the same priorities: number of eliminations before length, length before same number of eliminations and so on. Same preference order as AIC and other chaining. This may change the score and solve order of puzzles that require XY-Chains.
Also the old XY-Chain code was not using Windoku and Sudoku X diagonal units which was a big miss.
Currently XY-Chains do not use exotic links as this would turn a 'diabolical' strategy into an 'extreme' one.
Closed XY-Chains
September 2025. Here is a great observation I wished I'd picked up many years ago. Certainly dates from at least 2008 but other references please let me know! I'm grateful to Stefan in the Netherlands for emphasising how relevant it is and why it was missing from the solver. This is a good boost for XY-Chains and in testing I've found around 8%-10% additional eliminations. Indeed the old example 2 has the property described and I've moved it to this section. XY-Chains of this type now have no start or end cells highlighted.
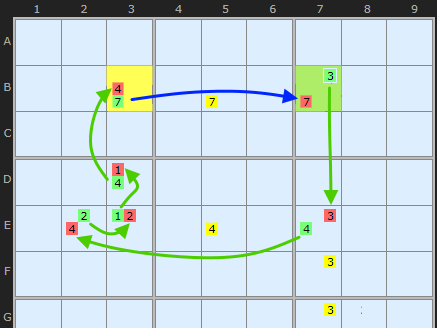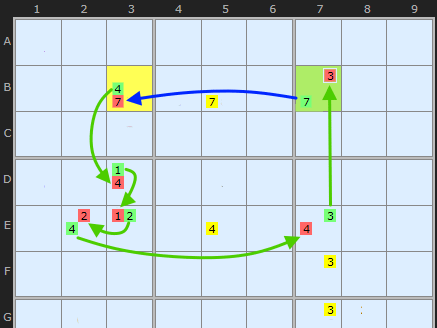
In this animation I've pulled out the essential parts of an XY-Chain from the following example. The chain starts on B3 and ends on B7. The old strategy would have eliminated the 7 in B5 and no more - since the rule is "at least one end of the chain or the other must be the solution".
But if the two ends of the chains can see each other we get a continuous loop. The blue arrow bridges the gap since the 7s in B3 and B7 connect. We are going to see this a lot in X-Cycles and later in Alternating Inference Chains. The difference is that Strong Links are all on the bi-value cells. The arrows in the diagram illustrate the direction of inferences.
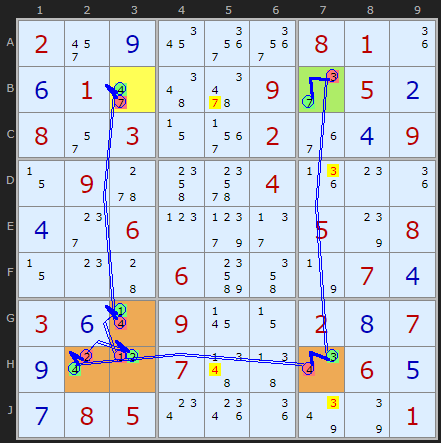
The alternating red and green candidates show us that all round the chain the solution must be one colour or another. We don't know which but we do know they form two distinct sets. All Weak Links become Strong Links which means we can eliminate along every link in the chain. So the 4 in H5 is knocked out by the link H27 and two 3s in D7 and J7 are knocked out by the link BH7.
This is Nice Loop Rule 1 This neatly ties together the family of chaining strategies.
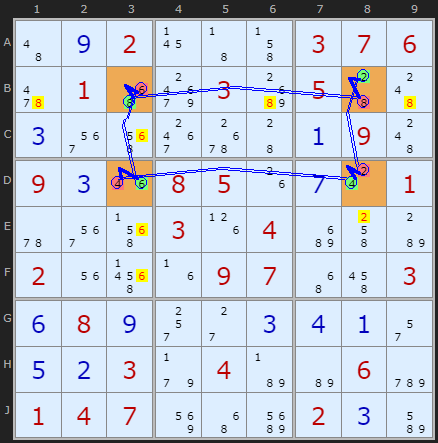
This Sudoku puzzle contains three XY-Chains, starting with this short rectangular one. Although this loop is continuous the solver needs to start somewhere and that is B3. That cell is either 8 or 6.
If it is 6 then D3 must be 4 which pushes 2 into D8 which in turn makes B8 8.
You can trace this from back round the other way:
If B3 is 8 then B8 must be 2 which pushes 4 into D8 which in turn makes B8 6 confirming B3 is 8.
So three of the four links that span rows and columns contain candidates we can remove, as shown.
XY-Chains Exemplars
These puzzles require the XY-Chains strategy at some point but are otherwise trivial.New examples added here as of August 2025
They make good practice puzzles.
- Exemplar 1 (x5, score 81)
- Exemplar 2 (x2, score 88)
- Exemplar 3 (x2, score 89)
- Exemplar 4 (x2, score 90)
- Exemplar 5 (x2, score 93)
- Exemplar 6 (x2, score 98)

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Eric Bryant
> There is also a side effect that URs and ALSs might be used in the links
> making a chain although it will be rare. In two minds about this since they
> are not part of the pattern but are logically fine.
Here's a potential argument for leaving URs out, or having the option to disable them:
https://www.sudokuwiki.org/sudoku.htm?bd=S9B4712060n070409024j43040709050203064309130206080n040z07040705080206010903060901050307020804020803040109050706130n0807091306040207060902041308130z1302040n0608071309
This is a partially generated puzzle from some software I've been developing. The program has yet to randomly add in enough clues to make a complete puzzle.
The Solution Count of 3 can quickly be verified by "solving" by hand; plug a 1, 3 or 8 into A1 and you'll quickly end up with a complete valid grid.
BUG and Unique Rectangles don't apply here, because the puzzle is not yet at the point of having a unique solution.
Accordingly, uncheck both these strategies (along with XY-Chain) and the puzzle won't be solvable.
Check off XY-Chain again though, and we do get a unique solution, due to XY-Chains now including URs.
It would be nice to not have XY-Chains include URs if Unique Rectangles are unchecked, to not come across "false positives" for a puzzle's solvability.
Don't know how doable this is in the solver though; depends on how everything works under the hood.
Would it be feasible to alter one strategy's implementation based on whether another strategy is checked or unchecked?
Would this even be a good idea, or counterintuitive & against the solver's design principles?
Another possibility could be to have separate checkboxes for XY-Chains with & without URs, similar to how X-Wing & Swordfish have both finned & unfinned variants.
Of course, it could be that incomplete puzzles like this example are outside the scope of what the solver is intended to do, and I shouldn't be trying to "solve" the unsolvable. :)
... by: BeyelerStudios
The first one with hinge in B4 and wings {B3,B6} and {D4} and non-restricted common digit 5. Note that the 5 is present in the hinge like your example 1 for a type 1 WXYZ-Wing but isn't present in B3 similar to example 3 for a type 1 WXYZ-Wing: "we don't have to worry about the common digit 'seeing' the brown cells as they don't have a common digit in them." This eliminates the 5 in A4.
The second one with hinge C7 and wings {C5,C9} and {G7} and non-restricted common digit 8 eliminates the 8 in A7.
Cheers and thanks for all your great explanations!
... by: VladFein
.....5..84.....3......312.6...56...12.4....3..17....9.8...5.76..7........92..3...
Thank you for your great site!
... by: Wolfgang M.
thanks for documenting these variety of possibilties to eliminate candidates.
When I was studying the XY-chain explanation,
I found a sentence, which is contradicting the examples shown as explanation:
"With Y-Chains the hinge was expanded to a chain of identical bi-value cells but in an XY-Chain these can be different - as long as there is one candidate to make all the links."
In all 3 examples only the first and last cell in a chain are having one common candidate.
Maybe that was a more restrictive version in the past, which has been simplyfied lateral.
Could you please include this to the rule, as it confused me, when I read the text the first times, until I recognized, that the limitation to all members of the chain isn't really neccesary.
Wolfgang
... by: Regan
I think there's a very long XY chain linker in this puzzle to get the original 47 pair to a 4 in the bottom left corner
47-71-19-92-27-74-43-39-93-39-97-94-42-27-74-47 cancels the 7
Am I right?
... by: Nick
... by: Andy Potvin
RU S# DL Technique Details (only showing steps requiring Dlevel>=UR1=9)
37 18 45 XYchain:8 eliminated 6 from p25 via chain p23 p53 p73 p93 p99 p39 p35 p45.
37 19 45 XYchain:8 eliminated 8 from p79 via chain p73 p53 p23 p26 p46 p45 p35 p39.
37 20 37 XYchain:5 eliminated 5 from p78 via chain p73 p93 p99 p39 p79.
37 21 37 XYchain:5 eliminated 2 from p19 p29 via chain p39 p99 p93 p73 p79.
37 22 37 XYchain:5 eliminated 8 from p19 via chain p39 p79 p73 p93 p99.
37 23 37 XYchain:5 eliminated 7 from p17 p27 p89 via chain p87 p99 p39 p79 p19.
And if I transform the matrix/puzzle (in MATLAB notation to transpose(fliplr(Mp))) my solver needs only 4 XYchain's: one 8-link followed by 3 5-link.
I haven't yet developed a function to find the "simplest" solution possible. (And I don't have any plans to develop such a function.)
Best,
Andy
... by: Pieter, Newtown, Oz
Where has my head been at? Only just discovered the new Fireworks strategy 8 months later!!!
Anyway, this comment is re a possible bug!? In your daily example for 2022-07-16, we reach this board which finds an XY-Chain length 9 eliminating the 6 in F7. However, the solver does so via 3 sides of a previously discovered X-Wing "box", whereas it could have simply gone via one side and been of length 7. Curious!
Kudos as always for your fantastic and always expanding Solver!!!
Ciao, Pieter
... by: Anonymous
... by: ush
XY-Chain
length=4, chain ends: B7 and J8
This proves 8 is the solution at one end of the chain or the other
-8[B7]+9[B7]-9[F7]+7[F7]-7[F8]+9[F8]-9[J8]+8[J8]
8 taken off A8
8 taken off G7
8 taken off J7
However cell B6 was also 89...so why can it be ignored as not the start or end of the '8 ' chain? I thought a chain has to go as far as it can before you decide where it started or ends.
... by: Bondye
... by: Gordon
... by: AB
... by: Mike Hopkins
XY chain: initial candidates X and Y are (5) and (3).
Chain is: A7(5,9), A5(2,9), A1(2,6), C2(5,6),
No other cell in the common scope of the two ends of that chain can be (5).
C7 was (3,5,9) is now (3,9)
XY chain: initial candidates X and Y are (5) and (6).
Chain is: C2(5,6), A1(2,6), A5(2,9), A7(5,9),
No other cell in the common scope of the two ends of that chain can be (5).
A3 was (2,4,5) is now (2,4)
C9 was (3,5,6) is now (3,6)
Happy to share the source code, it is (Ada)
... by: Robert
We can define links in two ways - they can be between the same value in two different cells in the same row, column, or box, or they can be between different values within the same cell. We get three of the strategies described at this website by using different definitions for strong and weak links.
(1) Strong links required to be between different cells, weak links also required to be between different cells - original "nice loops". In the database of 100 puzzles I am using, 60 are solved this way.
(2) Strong links can be either between different cells or within the same cell, weak links can also be either between different cells or within the same cell - alternating inference chain. Of my 100 puzzles, 89 are solved this way.
(3) Strong links required to be within the same cell, weak links required to be between different cells - xy_chain. Of my 100 puzzles, 45 are solved in this way.
In (3), "strong links" refer to links that are required to be strong, and "weak links" refer to those that are not required to be strong. If a "weak" link happens to be strong, it still follows the rule for weak links, not strong links.
But there are three other combinations of strategies that I don't see described at the website. However, it was a pretty each job to modify my alternating inference chain software to handle them.
(4) Strong links required to be between different cells, weak links required to be within the same cell. Of my 100 puzzles, 21 are solved this way.
(5) Strong links can be either between different cells or within the same cell, weak links are required to be between different cells. Of my 100 puzzles, 80 are solved this way.
(6) Strong links are required to be between different cells, weak links can be either between different cells or within the same cell. Of my 100 puzzles, 83 are solved this way.
So there are three additional strategies :) Although (1), (3), (4), (5), and (6) are also special cases of (2), alternating inference chains. Simple colouring is also a special case of nice loops, and therefore of alternating inference chains. Medusa without Rule 6 is also a special case of alternating inference chains.
And it is very useful to split strategies into X-cycles, Colouring, Medusa and all that, as it simplifies things and you can look for the more common patterns first.
... by: John
Can an XY-Chain therefore consist of as little as 3 cells?
... by: Eli
... by: pie314271
... by: Kavala
Often you can find an XY Chain, but it is one that does not result in an elimination.
This chain can still be useful, however, when combined with a 3D Medusa chain.
For example, if one end of the XY Chain has a known color that is part of a 3D Medusa
Chain, then the other end of the XY Chain can be assumed to be the opposite color.
This helps extend the reach of the 3D Medusa in situations where that is not possible
following the usual logic of the 3D Medusa.
... by: kvnviktor
in the third example, the death rectangle c12, g12, numbers 8 and 4 in the corners
... by: TG
... by: CH
... by: Mike Van Emmerik
Oops. I don't have time right now to sort out why, but it's not always that both ends can be filled in. So you just get the usual "must be opposite colour" information, and that often allows one end to be filled in, sometimes both.
... by: Mike Van Emmerik
"At first I select a bi value cell. Not anyone, but rather one containing two candidates regarding the digits missing the most. "
I agree that when attempting to solve puzzles manually (say with a phone app), it helps to cut down the forest of possibilities by considering first those bi-valued cells that there are less commonly represented. I now scan through the candidate numbers noting which numbers have the fewest unsolved cells. I'm not sure that both candidates for the initial bi-value cell need to be rare, just one of them. In fact, the last puzzle I did involved one of the rarer numbers paired with the most common unsolved number.
There is an additional "sanity check" that I like to perform. With the rarer numbers, there are often only a few viable starting pairs, and often some of these can be eliminated by eye as being involved in a strong link, or otherwise already related as opposite in colour. If you start with one such candidate bi-value cell, you are likely, after some effort, to prove something that you knew trivially to be true already. By contrast, if the candidates are already "like coloured" by simple colouring (X chains), meaning that you believe that one or the other is the solution, they make good candidates since if you can prove they are XY-chain linked (e.g.. this cell could be a 6, but if not it's a 4 so that has to be a 2 ... and this has to be a 6, then you've proved that each end is either a 6, or it's a 6. So both ends can be filled in. No doubt you can make stronger general statements about the other elements in the chain, but these tend to take care of themselves.
With these two checks reducing the effort needed to find these XY-chains, they are becoming more fun and much less of a chore.
... by: Steve
I believe I have found an alternative solution to Exemplar 3 on www.sudokuwiki.org/XY_Chains that requires only 1 XY-chain (or is it something else?) rather than four.
After all simpler strategies have been exhausted, I have the following chain:
1 on F2 -> 2 on F4 -> 8 on F8 -> 5 on F1 -> 4 on E3 -> 9 on E5
Alternatively, a 9 on F2.
So, any cell that can see F2 and E5 (i.e. E2 and F5) cannot contain a 9.
When I remove the 9s in these cells, the remainder of the Sudoku is solved with simple strategies.
I've checked this in the solver and it works. Have I got it right?
Cheers,
Steve Strain
Memphis, TN USA
... by: Eric
What is the additional condition to be statisfied by an XY-chain that is not met by the A1-A5 chain?
... by: Sherman
... by: Shum
... by: suneet shrotri
... by: gg fuller
... by: Guy Renauldon
This is to answer to François Tremblay and John Robinson question.
Yes François, there is a trick to discover an XY chain.
Recently, I settled a kind of method which I name the “Exclamation Mark Method”
That is what it is:
At first I select a bi value cell. Not anyone, but rather one containing two candidates regarding the digits missing the most.
Let’s say the cell I select contain “a” and “b” as candidates.
Then I make a double bet.
First bet: “a” true,
Second bet: “b” true.
Regarding the first bet, I draw a small vertical line “I” just under the “a” of the bet cell. Then I consider the other bi values cells only and I mark all the candidates deducted by this first bet by an “I”, drawn just under the candidates.
Regarding the second bet “b” I do the same but the mark will be a small point “.”under the “b” in the bet cell.
Most of the time, soon or later, if a XY chain exists, I obtain a cell containing a candidate marked with an exclamation mark “!” (This is the reason of the name of my “method”, although the exclamation mark can be reverse, the point on the top)
So a candidate , let’s say “k”, will be marked with an exclamation mark. It means it is true in both bets. So “k” is a true digit. (Although I can’t say anything on “a” or “b”). Most of the time, this true digit will solve the Sudoku, when the Sudoku is not difficult too much.
But I do not consider the job as finished. I have to find my XY chain.
Let’s see the simplest case at first: the cell where we have the “!” is a bi value cell too. I consider the other candidate in that cell, the one without the “!”, let’s say “m”. “m” have to be eliminated, so “m” must see two other bi value cells containing an “m”, which will be the two ends of my XY chain (to understand that, you have to know what an XY chain is exactly). Then I consider each end of my chain and I follow the reverse itinerary from each end. I draw the links between the bi value cells really, with a pen. Doing so I’ll automatically reach my double bet cell. And that it is, I’ve drawn my XY chain! Very easily, without the headaches y suffered before I applied that method. And doing so, you can find very long XY chains, containing ten links for example, or more.
Note that you can find a shorter chain which does not go through the double bet cell, but with the same ends. The reason is that more than one XY chain exists on a same grid most of the time.
If the cell which sees the two ends of the chain is not a bi value cell, it is a little bit more complicated. But the “method” works too. If the cell contains three candidates, you will have two candidates marked with an exclamation mark. Then the third candidate can be removed. If a cell contains four candidates, you’ll find three exclamation marks in that cell. Generally speaking, if the cell contains N candidates, you’ll find N-1 candidates with an exclamation mark. The other one left without the “!” can be removed. This chain does not give a true digit directly.
Sorry, I’ve been little bit long in my explanation, and please excuse my English, being French (perhaps François Tremblay will understand me better, his name sounding very French …)
I’d like to add some remarks, if Andrew Stuarts give me some more place.
1/An xy chain is in fact a multi value X Cycle in three dimension, containing bi values cells only from one end to the other. The strong links are located inside the bi value cells. The other links can be either strong or weak, except the links between “m”, which must be weak. In fact it is a special AIC, with bi value cells only.
3/ This “method” is not mine…in fact it is the well known Forcing Chain Strategy. But the exclamation mark trick is mine, I think.
Many thanks to Andrew Stuart if he accepts to publish my comment, which maybe he can find a bit too long and not very clear (it is to me, but may be not to all the readers due to my bad English…).
Guy Renauldon
... by: John Robinson
... by: S.Monta
First i would like to thank you very much for your great website witch made me dramatically improve my Sudoku skills.
I have a question : could the chain 56-67-67-78-83-89-96 be an XY-Chain?
... by: Marshal L. Merriam
Alternatively we could argue that the xy chain demands that at least one of the endpoints be a 2. Since they are the same, the cell must be a 2.
... by: Marshal L. Merriam
If C2 is not 5 then it must be 6. A1 cannot be 6, A5 cannot be 2 and A7 cannot be 9. Ergo, if C2 is not 5, then A7 must be 5. As noted in the first bullet, if A7 is not 5 then C2 must be 5. So either A7 or C2 must be 5.
When stated this way, the chain does not require locked sets. If C2 is not 5, then no other cell in box 1 can be 6, so even if there were a 6 at B3(say), all of the bullets would still hold.
... by: Marshal L. Merriam
If I haven't overlooked something, this allows XY chains to connect to other single number techniques that use strong link information (eg x- cycles, red-black)
... by: Matt Lala
Francois, I don't think you need a solver, but it does help to have a program that highlights all of them. I glance at the 'busiest' groupings of bivalue cells and then pick one and just start driving. If a fork presents itself I'll choose whichever option seems to steer me back towards the start of the chain.
Anton, I don't think they have to be locked, they just need to be bivalue. Try plugging in a 2 at the start of that chain in the 2nd example, and follow the links, and you'll see how the green cell at the end becomes a 6 (despite the unlocked cells used). And plugging in a 6 at the start makes the eliminations pretty obvious.
... by: Francois Tremblay
... by: Anton Delprado
An XY-Chain is possible from this although it would have the pivot chain below:
3A - 3C - 3H - 6H - 6F - 5F - 9F