SudokuWiki.org
Strategies for Popular Number Puzzles
AICs with Exotic Links
We have seen with ALSs and Unique Rectangles that it is possible to use some tricks to increase the availability of links to make chains. Going beyond simple alternating single digits is very useful for all chaining strategies. This particular one was inspired by an example puzzle sent in by Lane Walker in the USA. It actually had 45 solutions but an interesting Cell Forcing Chain nevertheless.
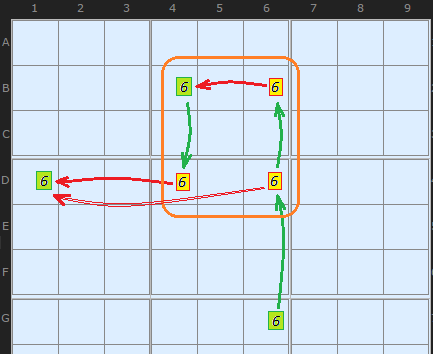
In this pattern the chain has reached (or started at) G6 on number 6 and the 6 is ON. Up column 6 are two more 6s which are turned OFF by G6. Under normal circumstances we could chain +6[G6] -6[B6] +6[B4] -6[D4] and that would be the end of it. The chain misses D6 even though we know that D6 must be OFF as well. Because we know that D1 is forced ON and the chain can continue.
My correspondent was quite correct to follow this logic but there is a branching here impossible to capture in the very linear way Alternating Inference Chains are built. AIC's can't do two OFFs to make a link.
The pattern considers four candidates N in a specific relationship to the input and output. The four candidates must be spread across two boxes and be in a different box from the input. If they were less separated they would be toggled en mass an you wouldn't need to employ this pattern. Also, two candidates N need to 'see' a third for an exit (output) and the other two need be a strong link, that is, B4 and B6 are the only two 6s in row B.
When and if I can fully implement Forcing Nets I think this sort of mini-loop or temporary branch will naturally come out in the wash, this sort of link probably being the simplest possible way a 'net' like pattern works, as opposed to the linear AIC. So it is easy to imagine extending this further to include more candidates and bigger patterns. For now the pattern is in the solver and some examples are now provided. In Ruud's top 50k stock I found 169 examples, so decent enough.
When and if I can fully implement Forcing Nets I think this sort of mini-loop or temporary branch will naturally come out in the wash, this sort of link probably being the simplest possible way a 'net' like pattern works, as opposed to the linear AIC. So it is easy to imagine extending this further to include more candidates and bigger patterns. For now the pattern is in the solver and some examples are now provided. In Ruud's top 50k stock I found 169 examples, so decent enough.
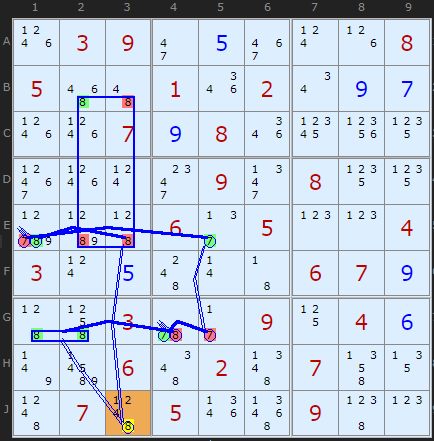
In example 1 an AIC is discovered on J3 using 8. Assuming it to be 8 we show by the chain that it cannot be so - therefore 8 can be removed.
+8[J3] -8(XW[-E3/-B3+B2-E2]) +8[E1]-7[E1]+7[E5]-7[G5] +7[G4]-8[G4]+8[G1|G2]-8[J3]
The example is orientated the same way as the pattern above. The input J3 picks up the four cells in BE23 and because of the number of 8s elsewhere in rows B and E, forces E1 to be ON for number 8. The chain continues back to J3.
I wondered what to call this pattern but I am a bit stumped. However I need a code in the results to draw the pattern correctly on the solver so I chose XW for X-Wing since this is a four cell formation, but it isn't quite the same. Any suggestions, happy to hear them.
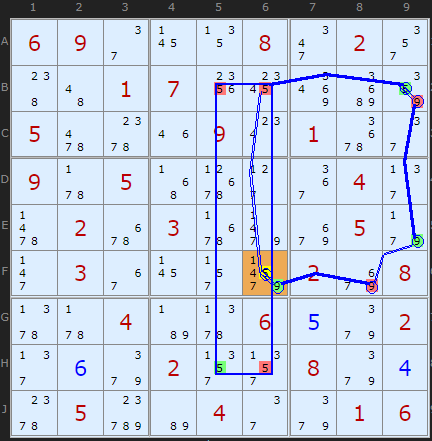
Example 2 is more spread out. It starts on F6 with 5 being ON. This goes straight into the pattern with the four cells BH56 and spitting out an +5 on B9
+5[F6]
-5(XW[-B6/-H6+H5-B5]) +5[B9]
-9[B9]+9[E9]-9[F8]+9[F6]-5[F6]
- Contradiction: When F6 is set to 5 the chain implies it cannot be 5 - it can be removed
You can see there are only three 5s in row B and two (the strong link) in row H.
Comments
... by: Anonymous
I think you are quite correct, you don't need them to line up in a rectangle. I also think that you don't necessarily need an X-Wing to make the link, any AIC or even fish would suffice.
Now we've come to the point where we form links in an AIC using an AIC itself. Good lord.
... by: Robert
In the first example, suppose the "6" in B4 were in A4 instead. It would still work, as long as A4 and B6 were the only "6" values in that box.
I've got my own solver running a far more general version of this - essentially, follow all the implications of choosing one candidate to be "on" or "off" (not just those along a particular chain), and when all but one candidate in a unit is "off", then the remaining one must be "on". (Also, if the only candidates in a unit that are not "off" by implication are in a group, then the group must be "on".) This solves some of the unsolveables. I need to get the output from this strategy into a readable form though, right now it's a total mess.
... by: Anonymous
For example in the first diagram, D1 is the fin and BD46 is the X-wing, which can be interpreted as a strong link.
This also means that Finned X-Wings are a subset of this strategy.
... by: Anonymous
By contrapositive, a false 6 in G6 implies a false 6 in D1.
Which means if the 6 in G6 is false, then an X-wing is formed at cells BD46, which makes the 6 in G6 false.
So you could consider this an AIC with an "almost X-wing" / "finned X-wing".