XY-Chains

XY-Chains is a way to connect two parts of the board that can't directly "see" each other. The "X" and the "Y" in the name represent these two values in each chain link. If we can connect the ends we can make inferences and eliminate candidates.

Originally these were found by extending Y-Wings into so-called Y-Wing Chains but it was quickly transformed into this more encompassing strategy. The same pincer-like attack on candidates that both ends can see by chaining bi-value cells. With Y-Chains the hinge relied on identical bi-value cells but in an XY-Chain the candidate can differ by one on each hop.

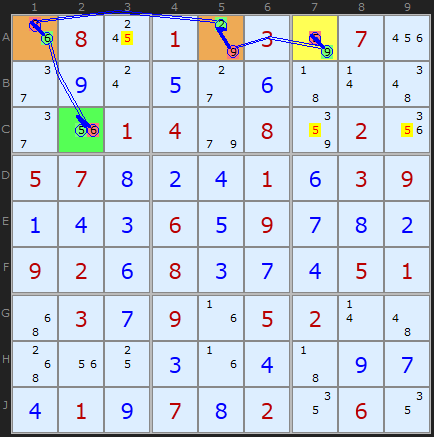
The example here is a very simple XY-Chain of length 4 which removed all 5's highlighted in yellow. The chain ends are 5 A7 and C2 - so all cells that can see both of these are under fire. It's possible to start at either end but lets follow the example from A7. We can reason as follows

• If A7 is 5 then A3/C7/C9 cannot be.
  
• if A7 is NOT 5 then it's 9, so A5 must be 2, which forces A1 to be 6. If A1 is 6 then C2 is 5.
  

Which ever choice in A7 the 5's in A3/C7/C9 cannot be 5. The same logic can be traced from C2 to A7 so the strategy is bi-directional, in the jargon.

The solver uses relatively simple chain notation with cells identified with [Row Letter+Column]. (There is an option to change to rYcX coordinates). In a chain we're alternating between strong and weak links but also turning candidates ON and OFF. To symbolise that the chain uses plus and minus. The number being turned on or off follows the symbol. The above example is
-5[A7]+9[A7]-9[A5]+2[A5]-2[A1]+6[A1]-6[C2]+5[C2]
5 taken off A3
5 taken off C7
5 taken off C9

In later documentation on Grouped X-Cycles you will see grouped cells denoted as +4[D4|E4] and when ALSs are used to make a link curly brackets are used: +7{H6|G6}. Rare exotic links like Unique Rectangles are named -9(UR[DF28]) as is an X-Wing -8(XW[-E3/-B3+B2-E2])

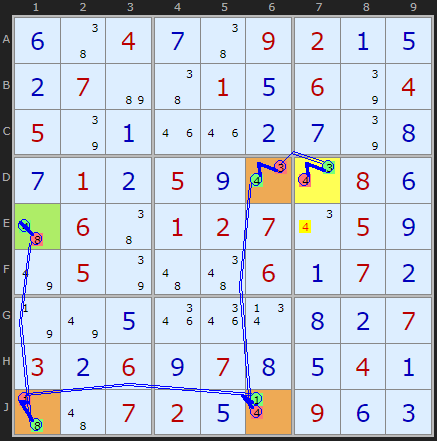
This relatively easy Sudoku puzzle contains contains a nice XY-Chain near the end. It proves 4 must be in either E1 or D7 and therefore we can remove the 4 in E7 since that cell can see both ends.

XY-Chains go way back to the earliest instance of the solver and had separate code for this strategy because the pattern is very simple and it pre-dates my work on AICs. But the selection of the “best” XY-Chain was very crude. I’d look for length 3 and return the first, then any length 4 and finally any length 5-12 and return the first. (Length here is the number of cells, not the chain links which are double the 'length').

I decided to see if I could use the AIC code to look for this pattern and re-use some code. The AIC Chain detection builds a list of the best 50 chains and allows the solver to “explore” other chains at the same step. This means XY-Chains share the same priorities: number of eliminations before length, length before same number of eliminations and so on. Same preference order as AIC and other chaining. This may change the score and solve order of puzzles that require XY-Chains.

Also the old XY-Chain code was not using Windoku and Sudoku X diagonal units which was a big miss.

There is also a side effect that URs and ALSs might be used in the links making a chain although it will be rare. In two minds about this since they are not part of the pattern but are logically fine. David Hollenberg found an example (choose second chain nect to 'explore').

September 2025. Here is a great observation I wished I'd picked up many years ago. Certainly dates from at least 2008 but other references please let me know! I'm grateful to Stefan in the Netherlands for emphasising how relevant it is and why it was missing from the solver. This is a good boost for XY-Chains and in testing I've found around 8%-10% additional eliminations. Indeed the old example 2 has the property described and I've moved it to this section. XY-Chains of this type now have no start or end cells highlighted.

It all rests on whether the ends of the chain can see each other.

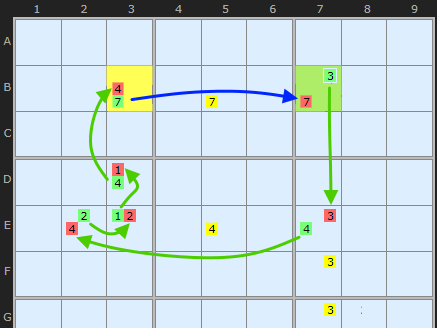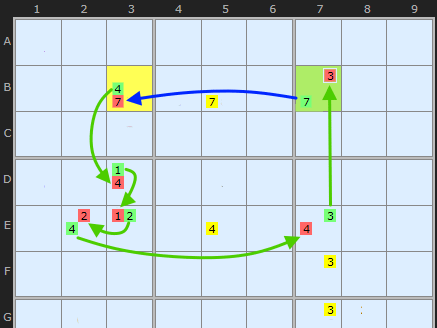
In this animation I've pulled out the essential parts of an XY-Chain from the following example. The chain starts on B3 and ends on B7. The old strategy would have eliminated the 7 in B5 and no more - since the rule is "at least one end of the chain or the other must be the solution".

But if the two ends of the chains can see each other we get a continuous loop. The blue arrow bridges the gap since the 7s in B3 and B7 connect. We are going to see this a lot in X-Cycles and later in Alternating Inference Chains. The difference is that Strong Links are all on the bi-value cells. The arrows in the diagram illustrate the direction of inferences.

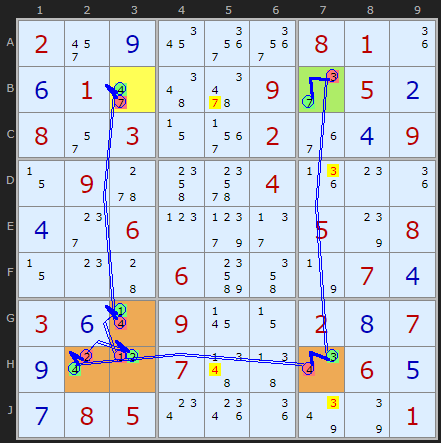
The alternating red and green candidates show us that all round the chain the solution must be one colour or another. We don't know which but we do know they form two distinct sets. All Weak Links become Strong Links which means we can eliminate along every link in the chain. So the 4 in E5 is knocked out by the link E27 and two 3s in F7 and G7 are knocked out by the link BE7.

This is Nice Loop Rule 1 This neatly ties together the family of chaining strategies.

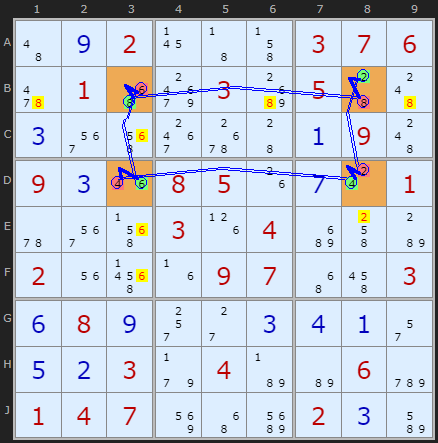
This Sudoku puzzle contains three XY-Chains, starting with this short rectangular one. Although this loop is continuous the solver needs to start somewhere and that is B3. That cell is either 8 or 6.

If it is 6 then D3 must be 4 which pushes 2 into D8 which in turn makes B8 8.

You can trace this from back round the other way:

If B3 is 8 then B8 must be 2 which pushes 4 into D8 which in turn makes B8 6 confirming B3 is 8.

So three of the four links that span rows and columns contain candidates we can remove, as shown.

XY-Chains Exemplars

These puzzles require the XY-Chains strategy at some point but are otherwise trivial.
New examples added here as of August 2025
They make good practice puzzles.

• Exemplar 1 (x5, score 81)
• Exemplar 2 (x2, score 88)
• Exemplar 3 (x2, score 89)
• Exemplar 4 (x2, score 90)
• Exemplar 5 (x2, score 93)
• Exemplar 6 (x2, score 98)