by James Pike

During some recent re-coding of sections of my Sudoku program, I noticed enough similarities of required function, to combine routines to include Doubles, Triples and Quads (DTQ), both hidden and naked in the same algorithm. A little later, I was re-coding the X-wing section and decided to generalize to include both the vertical and horizontal orientation. Then the routine got a little more generalized to include Swordfish and Jellyfish (XSJ), both vertical and horizontal. It eventually became apparent that a single set of logic could solve for Doubles, Triples and Quads, both hidden and naked, as well as X-wing, Swordfish and Jellyfish, both vertical and horizontal.

Input to Related Sets is a 9x9 data array composed of a column, row, box or digit slice from the candidate matrix (see Multiples article), together with the identity of the source, such as column 1. The set of routines eliminates candidates as described below and can provide a detailed audit trail of the deletions and their justification.

The essence of hidden DTQ is that all of the qty(2), qty(3) or qty(4) digits from each set (columns, rows, boxes) occupy only qty cells, and thus define the cells. Any other digits in those cells can be deleted. Naked is when qty cells have only qty digits and therefore define the cells. Any other occurrences of those digits in the set can be deleted. DTQ concerns all digits at once, the data is digit x cell for a column, row or box set.

The X-wing family looks at only one digit at a time and is looking for qty(2, 3 or 4) columns with the digit (vertical orientation) that in total contain only qty rows with the digit. These conditions form a closed set, so any other occurrences of the digit in those rows - but not the columns - can be deleted. Horizontal orientation wants qty rows that in total contain only qty cols. The data is column x row for a digit.

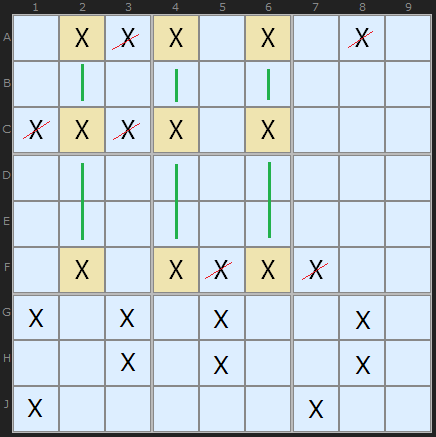
The diagram (right) typifies the total logic requirement to identify all of the triple and swordfish structures and the candidate eliminations that they justify: 3 columns that, in total, intersect 3 rows, allowing the deletion of extra entries in only those rows. When the same rules are applied for 2 and 4 columns, and the array is transposed each time, the analysis is complete for all DTQ and XSJ in both orientations. This algorithm provides that function.

By using a 9x9 array as the basis for analysis, the input data from the different sources are just slices from the candidate array. Deletions can be mapped back to the candidate array (9x9x9 - col,row,digit). For DTQ, the columns represent digits and the rows represent sequence number within the set (cell#, or cell). This gives the required digit x cell content that is required. In practice, these are all simple candidate slices except for boxes, which require minor concatenation. The setup for the work array for XSJ is just a digit slice from the candidate array.

The basic purpose of the related sets algorithm is to identify situations where 2, 3 or 4 columns in the array have values at the exact same number of rows - in total. Such structures allow for candidate deletions when there are extra values in the selected rows (only). These multiples (for want of a better term) are known as doubles, triples and quads when the data is in the digit x cell plane, and known as X-Wing, Swordfish and Jellyfish when the data is in the column x row plane, but their identification is identical in the work array.

If the related sets algorithm knows the source of the data, it can perform any deletes that it justifies in the candidate matrix. In the XSJ situation, it already has the column and row information and simply needs to calculate the digit. For DTQ, it has the digit and if it knows the column, row or box number (source), it can map from source and cell number to column and row.

A nice advantage of this algorithm is that to switch from hidden/vertical orientation to naked/horizontal, all that needs be done is to transpose (swap axes) the work array.

A work array of dummy data for descriptive purposes only, is pictured below, along with its column and row totals.

0 0 0 1 0 1 0 0 0 2
1 0 0 1 0 0 1 1 0 4
0 0 0 0 0 0 0 0 0 0
1 0 1 0 0 1 0 0 0 3
0 0 0 1 0 0 1 0 0 2
0 0 0 0 0 0 0 0 0 0
0 0 1 0 0 1 1 1 0 4
0 0 1 1 0 0 0 0 0 2
0 0 1 0 0 1 0 0 0 2
2 0 4 4 0 3 2 2 0

Input

Input variables are:
Input variable is: work (the name of the 9x9 data array), source (column, row, square, digit), value (of source).

Function

The routine will check work for multiples structures in both orientations. If it finds any of these structures, it then checks to see if any deletions will result and makes them.

Output

Sufficient information is made available for a comprehensive audit trail using the traditional terms for the structures as deletions are made.

Analysis

1. Quantity is cycled from 2 up to 4 as the outer loop - 3 cases


2. Orientation is cycled next - normal or transposed. This multiplies the cases tested to 6 for each array. The discussion that follows is for each case.


3. If any row or column has a total of 1, that is a "single" situation, this array is abandoned to let the singles routine pick it up.


4. Remove columns that total more than quantity row intersections - they can’t be part of a solution.


5. At any time in the process, if the total number of non-zero cols or rows falls below quantity, the case analysis is finished with a negative result.


6. At any time in the process, if the total number of non-zero cols equals quantity and the total number of non-zero rows equals quantity, a solution has been found.


7. Whenever a solution is found, it is tested to see if deletions would arise and they are made. The test is simple. If any selected row has a greater total than quantity, there are deletions to be made.


8. "Impossible" columns are removed next. A column is deemed impossible if it doesn’t have enough compatible columns to make up quantity for a solution. Columns have sets of occupied rows. For example, column 1’s set is {2,4}. Columns are deemed incompatible if their combined sets (the total set of unique numbers) exceeds quantity. If quantity is 3, column 3 is not compatible with column 1 because their combined set is 5 in length {2,4,7,8,9}. At a quick glance, the only column that is compatible with column 1, would be column 8 {2,4,7}, and therefore column 1 could be deleted for this case.


9. At this stage, the vast proportion of cases have been resolved (apparently >95%), so the more laborious next step is saved till last.


10. We are now looking for a combination of 2, 3, or 4 columns (depending on quantity) out of a greater number of possible columns. The routine generates every possible permutation for testing to see if it can find quantity columns with a combined set of quantity rows that has consequent deletions.

Note that the routine doesn’t care if it is working on DTQ or XSJ. They are the same in the array’s plane - multiples.

Jamie Pike
August 2016