W-Wing Strategy

W-Wings are part of the 'Bent Sets' family have been around for a long time [see 1, 2 and 3]. I was late to the party even in 2014 when I coded them into the solver but I felt they were overlapping with several other chaining strategies so didn't include it in the main Sudoku solver until now (January 2026).

But it is helpful to the human solver to know as many stand-out strategies as possible and these are relatively easy and can go early in the 'tough' order of strategies. I'll explain the impact with some stats later in the article.

For the time being I'm introducing them just to the Sudoku Solver.
If anyone knows why they are called W-Wings, do let me know.

To explain this strategy it is worth discussing the exception rather than the rule. Consider this 'tough' puzzle at this point. There happen to be a lot of 4/9 cells on the board. Pairs like this don't appear in isolation - if there are two in the same row, column or box they would be Naked Pairs and we'd have used them to remove other 4s and 9s in those units. But we are past that point.

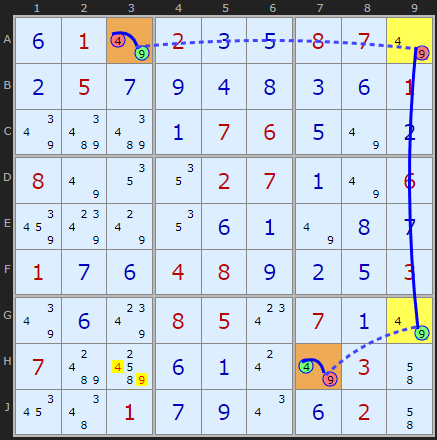
Instead we can check if there are two cells with 4 and 9 that can't see each other (not a conjugate pair) but can be connected to each other using other 4+9 cells. This is the case with A3 and H7. They are connected by strong links via A9 and G9. The solver is displaying an alternating strong/weak chain not just because weak links can be strong but because we alternate on and off. The solver is showing one of four possible chains logic:

• A3 is 4 implying H7 must be not 4, so 9.
• A3 is 9 implying H7 must be not 9, so 4.
• A3 is not 4 (must be 9) implying H7 must be 4.
• A3 is not 9 (must be 4) implying H7 must be 9.

Any of these are proofs. It means that any cell that can see both ends of the chain cannot have a 4 or a 9. Such as cell is H3

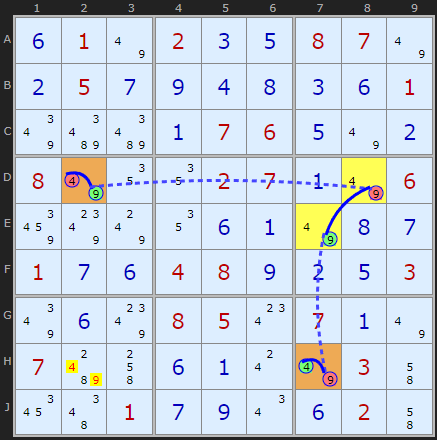
In the very next step is another elimination of 4s and 9s, this time in H2. A slightly different set of cells but I'm sure the pattern and logic is clear.

The name for this pattern is a Remote Pair Chain. A more convoluted explanation for this appears here as Remote Pairs. A long time ago I removed it from the solver as it was wholly a subset of XY-Chains. But length-4 version it is still simple to spot and worth using before the broader XY-Chain logic is invoked.

Using this pattern three times saves six Rectangle Eliminations. Untick W-Wings and try.

Note: Remote Pairs can be more than four cells long. But the next size is six and then eight - so even numbers. The coincidence of so many identical bi-values cells means they are increasingly rare at longer lengths but keep an eye out.

So what does this have to do with 'W-Wing'?

In this puzzle we've found two cells with 3 and 6 in them - cells A6 and F5. They cannot see each other. We cannot connect them through 3 but we can connect them through a strong link on 6 (the yellow cells).

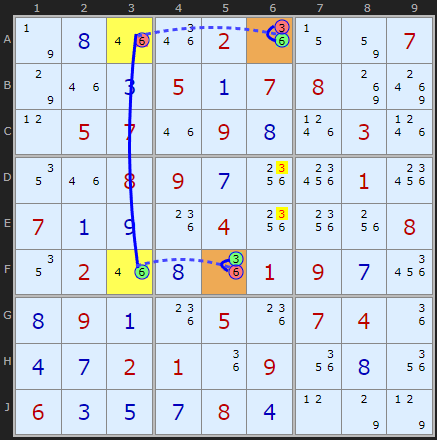
If A6 is not a 3 it must be 6. That gives us a weak link from +6 to -6 in A3. -6 in A3 forces +6 in F3 - a strong link (this is the important - it must be strong). +6 in F3 removes 6 in F5 making it 3. Reverse the chain logic and we prove that 3 must be in one of those orange cells. There are two cells that can see both ends and contains 3 - D6 and E6 and we can remove 3 from them.

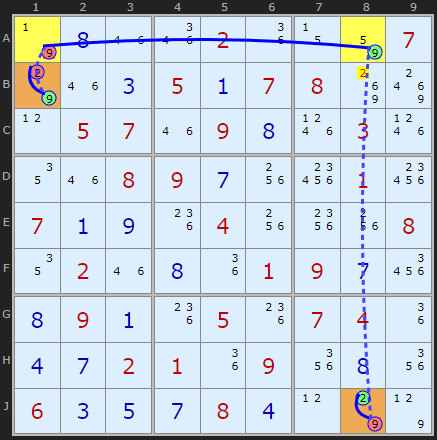
We can go again in the very next step. This time it is {2/9} in B1 connected to J8 via the strong link on 9 between A1 and A8. Trace the logic in both directions to satisfy yourself that one end of the W-Wing (orange cells) must be 2.

It might be clear now that if all the cells share the same digits you have two mirrored Single W-Wings and therefore a Double or a Remote Pair Chain.

There is one further W-Wing after this step. See if you can spot it.

There is one more configuration that should be mentioned. It is possible there are two W-Wings using the same start and end cell but they route through different intermediaries. We can catch these at the same time if we are careful. Thanks to Andy Potvin for pointing these out.

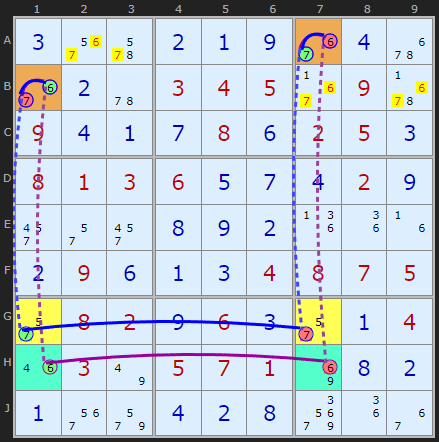
If 6 is going to be the solution in B1 that places 7 in A7 - this is connected through the strong link G1<=>G7
Or if 7 is in B1 then 6 must be the solution in A7. But this inference is connected through a different strong link H1<=>H7

We have two inference chains allowing simultaneous eliminations on 6 and 7 for all cells that can see B1 and A7.

-6[A7]+7[A7]-7[G7]+7[G1]-7[B1]+6[B1]
-7[A7]+6[A7]-6[H7]+6[H1]-6[B1]+7[B1]

(Note because the blue chain is drawn second it asserts the red/green circles of the candidates so might look a bit odd for +6[A7] to -6[H7] to be both red 6s)

Here is a diabolical puzzle with two split double W-Wings. See if you can spot them.

I've tested the strategy on two datasets. Andy Potvin has been a strong advocate for this strategy and I initially placed it just before Y-Wings. This is appropriate for the easy-to-spot Remote Pair types but I've now moved it after Y-Wings as at least half of the examples I find are more complex.

There is the 17-clue set containing all 31,512 sudoku puzzles with 17 clues. Most are easy but it is a fun and useful set to test with. The second is Ruud's top 50,000 from way back when. I might run some stats again on a randomly generated stock.

The evaluation here is when W-Wings are just after Y-Wings

The solver distinguishes between Double, Single and Split W-Wings. The double (RP4) type I find about 600 in the 17-clue set so relatively rare. There were 950 proper W-Wings in Just17 and 39 split doubles. In Ruud's set I found 16,053 puzzles with W-Wings and it was used 20,181 times. The vast majority Single W-Wings, RP4=806 and Split=271.

The largest declines in other strategies have been Rectangle Eliminations (8%), Simple Colouring (5%), XYZ-Wings (9%) and XY-Chains (12%), 3D Medusa (6%) but this is highly sensitive to ordering. Chute Remote Pairs also go down if evaluated after W-Wings and Y-Wings by 11% if used after W-Wings.

The top 50k set with W-Wings required 3,022 more strategy steps than without, a 0.1% increase. That suggests most of the W-Wings are contributing to a solve path, but there are always multiple solve paths.

In terms of score I've used the same points as Chute Remote Pairs and overall I see a score reduction in about 75% of puzzles that use against a 25% increase in score. So mixed results. This is inline with instinct that it is nice to have but not always a better performance.

---

³Ken Reek's (SudoKoach v2.5) User's Guide pp.47-50