KenKen Dog Legs
I coined 'dog legs' back when I was making and solving Killer Sudoku. Some Killer Sudoku puzzles will contain cages which span three boxes and these can potentially contain two numbers which are the same. The convention with Killer Sudoku (which I certainly adhere to, but others may not), is that whatever permissable combinations (see the article KenKen Combinations) in that cage, no combinations will contain duplicate numbers. These cages look like they 'dog leg' across boxes.
With KenKen and KenDoku 'dog leg' cages are extremely common and are part of the puzzle. Combinations of numbers can potentially contain duplicates and even double duplicates and triplets. Some examples are below.
It is helpful to spot these dog legged cages since the number of combinations you will have to consider will increase and I treat these differently using yellow in the hover over.
With KenKen and KenDoku 'dog leg' cages are extremely common and are part of the puzzle. Combinations of numbers can potentially contain duplicates and even double duplicates and triplets. Some examples are below.
It is helpful to spot these dog legged cages since the number of combinations you will have to consider will increase and I treat these differently using yellow in the hover over.
The 4x is a simple one where the duplicates must be placed diagonally from each other. However we don't know if they must be two 2s or two 1s.
The 36x contains combinations with duplicates and one without. It will be the solvers task to decide which is right.
To contrast these, the simple two cell cages such as the 6x highlighted can't contain combinations with duplicates. Therefore the hover-over on the solver is a different colour.
See the article on KenDoku Dog Legs for a distinction between the two types of puzzles.
To be complete I have created this diagram which shows all the possible cage shapes with the maximum number of duplicate positions. These are labelled A and B - since some cages we can have more than one duplicate solution number.
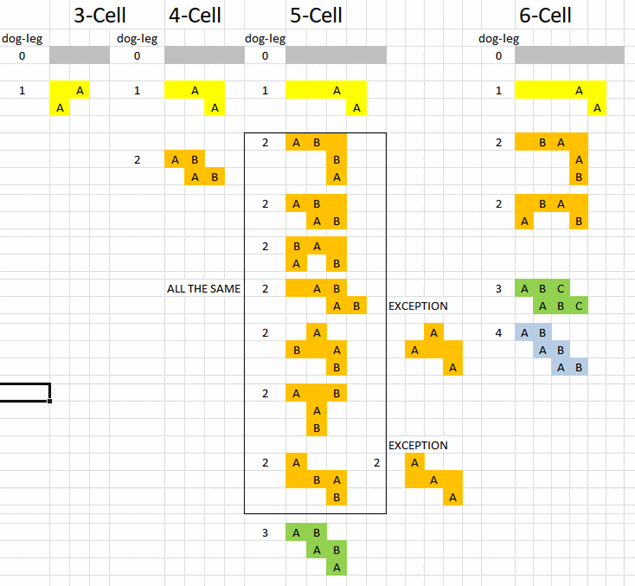
To be complete I have created this diagram which shows all the possible cage shapes with the maximum number of duplicate positions. These are labelled A and B - since some cages we can have more than one duplicate solution number.


Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: Edmund
I have had a cage of 13 with 2 cells in first row and 1 cell in second row. The answers should be 4,6 and 3. But at the first few steps of the solver, it claims that all numbers should be removed from the cells. Would you please help explain or if there is a bug?
Load Puzzle
(I was just designing the kenken. I'm not sure if the puzzle yields a unique solution).